Статистика — распределение Рэлея

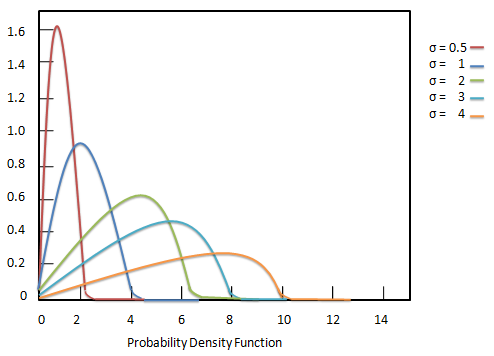
Распределение Рэлея является распределением непрерывной функции плотности вероятности. Он назван в честь английского лорда Рэлея. Этот дистрибутив широко используется для следующих целей:

• Связь — для моделирования множества путей густо рассеянных сигналов при достижении приемника.

• Физические науки — для моделирования скорости ветра, высоты волн, звукового или светового излучения.

• Инжиниринг — проверка срока службы объекта в зависимости от его возраста.

• Медицинская визуализация — для моделирования дисперсии шума в магнитно-резонансной томографии.

Связь — для моделирования множества путей густо рассеянных сигналов при достижении приемника.

Физические науки — для моделирования скорости ветра, высоты волн, звукового или светового излучения.

Инжиниринг — проверка срока службы объекта в зависимости от его возраста.

Медицинская визуализация — для моделирования дисперсии шума в магнитно-резонансной томографии.

Функция плотности вероятности распределения Рэлея определяется как:

формула

${f (x; \ sigma) = \ frac {x} {\ sigma ^ 2} e ^ {\ frac {-x ^ 2} {2 \ sigma ^ 2}}, x \ ge 0}$

Где —

• ${\ sigma}$ = масштабный параметр распределения.

${\ sigma}$ = масштабный параметр распределения.

Функция распределенного распределения Рэлея определяется как:

формула

${F (x; \ sigma) = 1 - e ^ {\ frac {-x ^ 2} {2 \ sigma ^ 2}}, x \ in [0 \ infty}$

Где —

• ${\ sigma}$ = масштабный параметр распределения.

${\ sigma}$ = масштабный параметр распределения.

Дисперсия и ожидаемая стоимость

Ожидаемое значение или среднее значение распределения Рэлея определяется как:

${E [x] = \ sigma \ sqrt {\ frac {\ pi} {2}}}$

Дисперсия распределения Рэлея определяется как:

${Var [x] = \ sigma ^ 2 \ frac {4- \ pi} {2}}$