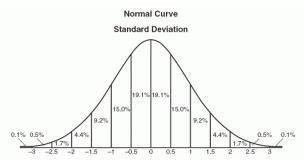
Нормальное распределение — это расположение набора данных, в котором большинство значений кластеризуется в середине диапазона, а остальные сужаются симметрично в любую крайнюю сторону. Рост — один простой пример чего-то, что следует нормальному распределению: большинство людей среднего роста число людей, которые выше и ниже среднего, довольно равны, и очень небольшое (и все еще приблизительно эквивалентное) число людей либо чрезвычайно высоко, либо крайне мало. Вот пример кривой нормального распределения:
Графическое представление нормального распределения иногда называют кривой колокола из-за его расширяющейся формы. Точная форма может варьироваться в зависимости от распределения населения, но пик всегда находится посередине, а кривая всегда симметрична. В нормальном распределении значение режим и медиана все одинаковы.
формула
y= frac1 sqrt2 pie frac−(x− mu)22 sigma
y= frac1 sqrt2 pie frac−(x− mu)22 sigma
Где —
-
mu = Среднее
-
sigma = стандартное отклонение
-
pi ок3.14159
-
e ок2.71828
mu = Среднее
sigma = стандартное отклонение
pi ок3.14159
e ок2.71828
пример
Постановка задачи:
Обследование ежедневного времени в пути имело следующие результаты (в минутах):
| 26 | 33 | 65 | 28 | 34 | 55 | 25 | 44 | 50 | 36 | 26 | 37 | 43 | 62 | 35 | 38 | 45 | 32 | 28 | 34 |
Среднее значение составляет 38,8 минуты, а стандартное отклонение — 11,4 минуты. Преобразуйте значения в z-оценки и подготовьте график нормального распределения.
Решение:
Формула для z-счета, которую мы использовали:
z= fracx− mu sigma
z= fracx− mu sigma
Где —
-
z = «z-оценка» (стандартная оценка)
-
x = значение, которое будет стандартизировано
-
mu = среднее
-
sigma = стандартное отклонение
z = «z-оценка» (стандартная оценка)
x = значение, которое будет стандартизировано
mu = среднее
sigma = стандартное отклонение
Чтобы преобразовать 26:
Сначала вычтите среднее: 26-38,8 = -12,8,
Затем разделите на стандартное отклонение: -12,8 / 11,4 = -1,12
Таким образом, 26 равно -1.12 стандартного отклонения от среднего
Вот первые три преобразования.
| Исходное значение | расчет | Стандартный счет (z-счет) |
|---|---|---|
| 26 | (26-38,8) / 11,4 = | -1,12 |
| 33 | (33-38,8) / 11,4 = | -0,51 |
| 65 | (65-38,8) / 11,4 = | -2,30 |
| … | … | … |
И вот они графически представляют: