Учебники

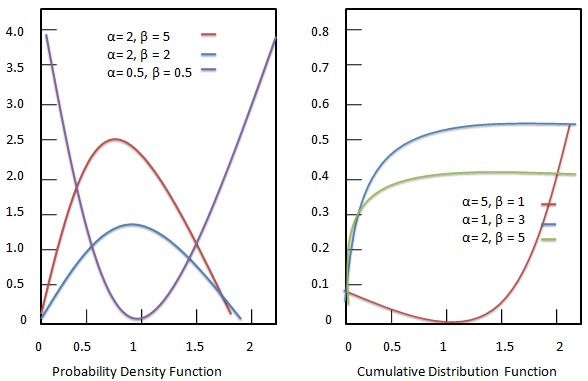
Статистика — Бета Распределение

Ноябрь 5, 2018

Бета-распределение представляет собой непрерывное распределение вероятностей, параметризованное двумя положительными параметрами формы, $ \ alpha $ и $ \ beta $, которые отображаются как показатели случайной величины x и управляют формой распределения.

Бета Распределение

Функция плотности вероятности

Функция плотности вероятности бета-распределения имеет вид:

формула

$ {f (x) = \ frac {(xa) ^ {\ alpha-1} (bx) ^ {\ beta-1}} {B (\ alpha, \ beta) (ba) ^ {\ alpha + \ beta- 1}} \ hspace {.3in} a \ le x \ le b; \ alpha, \ beta> 0 \\ [7pt] \, где \ B (\ alpha, \ beta) = \ int_ {0} ^ {1} {t ^ {\ alpha-1} (1-t) ^ { \ beta-1} dt}} $

Где —

  • $ {\ alpha, \ beta} $ = параметры формы.

  • $ {a, b} $ = верхняя и нижняя границы.

  • $ {B (\ alpha, \ beta)} $ = Бета-функция.

$ {\ alpha, \ beta} $ = параметры формы.

$ {a, b} $ = верхняя и нижняя границы.

$ {B (\ alpha, \ beta)} $ = Бета-функция.

Стандартная бета-версия

В случае если верхняя и нижняя границы равны 1 и 0, бета-распределение называется стандартным бета-распределением. Это обусловлено следующей формулой:

формула

$ {f (x) = \ frac {x ^ {\ alpha-1} (1-x) ^ {\ beta-1}} {B (\ alpha, \ beta)} \ hspace {.3in} \ le x \ ле 1; \ alpha, \ beta> 0} $

Кумулятивная функция распределения

Кумулятивная функция распределения бета-распределения определяется как:

формула

$ {F (x) = I_ {x} (\ alpha, \ beta) = \ frac {\ int_ {0} ^ {x} {t ^ {\ alpha-1} (1-t) ^ {\ beta- 1} dt}} {B (\ alpha, \ beta)} \ hspace {.2in} 0 \ le x \ le 1; p, \ beta> 0} $

Где —

  • $ {\ alpha, \ beta} $ = параметры формы.

  • $ {a, b} $ = верхняя и нижняя границы.

  • $ {B (\ alpha, \ beta)} $ = Бета-функция.

$ {\ alpha, \ beta} $ = параметры формы.

$ {a, b} $ = верхняя и нижняя границы.

$ {B (\ alpha, \ beta)} $ = Бета-функция.

Это также называется неполным коэффициентом бета-функции.

50
Share: