Статистика — гамма-распределение

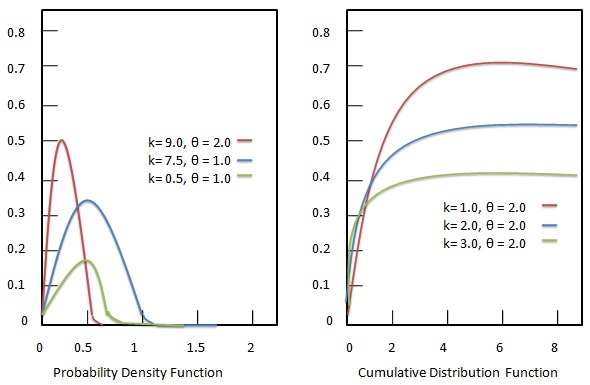
Гамма-распределение представляет собой непрерывные вероятностные распределения двухпараметрического семейства. Распределения гаммы разработаны, как правило, с тремя видами комбинаций параметров.

• Параметр формы $k$ и масштабный параметр $\ theta$.

• Параметр формы $\ alpha = k$ и параметр обратного масштаба $\ beta = \ frac {1} {\ theta}$, называемый параметром скорости.

• Параметр формы $k$ и средний параметр $\ mu = \ frac {k} {\ beta}$.

Параметр формы $k$ и масштабный параметр $\ theta$.

Параметр формы $\ alpha = k$ и параметр обратного масштаба $\ beta = \ frac {1} {\ theta}$, называемый параметром скорости.

Параметр формы $k$ и средний параметр $\ mu = \ frac {k} {\ beta}$.

Каждый параметр представляет собой положительные действительные числа. Гамма-распределение — это максимальное распределение вероятностей энтропии, определяемое следующими критериями.

формула

$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ and \ is \ fixed. \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha) — ln (\ beta) \ и \ is \ fixed. } $

Где —

• ${X}$ = Случайная переменная.

• ${\ psi}$ = функция дигаммы.

${X}$ = Случайная переменная.

${\ psi}$ = функция дигаммы.

Характеризация с использованием формы $\ alpha$ и скорости $\ beta$

Функция плотности вероятности

Функция плотности вероятности гамма-распределения имеет вид:

формула

Где —

• ${\ alpha}$ = параметр местоположения.

• ${\ beta}$ = параметр масштаба.

• ${x}$ = случайная величина.

${\ alpha}$ = параметр местоположения.

${\ beta}$ = параметр масштаба.

${x}$ = случайная величина.

Кумулятивная функция распределения

Кумулятивная функция распределения гамма-распределения задается как:

формула

${F (x; \ alpha, \ beta) = \ int_0 ^ xf (u; \ alpha, \ beta) du = \ frac {\ gamma (\ alpha, \ beta x)} {\ Gamma (\ alpha)} }$

Где —

• ${\ alpha}$ = параметр местоположения.

• ${\ beta}$ = параметр масштаба.

• ${x}$ = случайная величина.

• ${\ gamma (\ alpha, \ beta x)}$ = неполная нижняя гамма-функция.

${\ alpha}$ = параметр местоположения.

${\ beta}$ = параметр масштаба.

${x}$ = случайная величина.

${\ gamma (\ alpha, \ beta x)}$ = неполная нижняя гамма-функция.

Характеризация с использованием формы $k$ и масштаба $\ theta$

Функция плотности вероятности

Функция плотности вероятности гамма-распределения имеет вид:

формула

Где —

• ${k}$ = параметр формы.

• ${\ theta}$ = масштабный параметр.

• ${x}$ = случайная величина.

• ${\ Gamma (k)}$ = гамма-функция, оцененная в k.

${k}$ = параметр формы.

${\ theta}$ = масштабный параметр.

${x}$ = случайная величина.

${\ Gamma (k)}$ = гамма-функция, оцененная в k.

Кумулятивная функция распределения

Кумулятивная функция распределения гамма-распределения задается как:

формула

${F (x; k, \ theta) = \ int_0 ^ xf (u; k, \ theta) du = \ frac {\ gamma (k, \ frac {x} {\ theta})}} {\ Gamma (k )}}$

Где —

${k}$ = параметр формы.

${\ theta}$ = масштабный параметр.

${x}$ = случайная величина.

${\ gamma (k, \ frac {x} {\ theta})}$ = неполная нижняя гамма-функция.