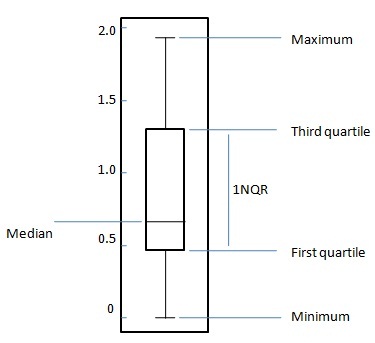
Квадратный график — это стандартизированный способ отображения распределения данных на основе следующих пятизначных сводок.
-
минимальный
-
Первый квартиль
-
медиана
-
Третий квартиль
-
максимальная
минимальный
Первый квартиль
медиана
Третий квартиль
максимальная
Для равномерно распределенного набора данных на блок-диаграмме центральный прямоугольник охватывает первый квартиль до третьего квартиля (или межквартильный диапазон, IQR). Линия внутри прямоугольника показывает медиану, а «усы» над и под рамкой — расположение минимальных и максимальных значений. Такой блок-график отображает полный диапазон изменения от минимального до максимального, вероятный диапазон изменения, IQR и медиану.
Постановка задачи:
Создайте коробочную диаграмму для следующих двух наборов данных.
| 0,22 |
| -0,87 |
| -2,39 |
| -1,79 |
| 0,37 |
| -1,54 |
| 1,28 |
| -0,31 |
| -0,74 |
| 1,72 |
| 0,38 |
| -0,17 |
| -0,62 |
| -1,10 |
| 0,30 |
| 0,15 |
| 2,30 |
| 0,19 |
| -0,50 |
| -0,09 |
| -5,13 |
| -2,19 |
| -2,43 |
| -3,83 |
| 0,50 |
| -3,25 |
| 4,32 |
| 1,63 |
| 5,18 |
| -0,43 |
| 7,11 |
| 4,87 |
| -3,10 |
| -5,81 |
| 3,76 |
| 6,31 |
| 2,58 |
| 0,07 |
| 5,76 |
| 3,50 |
Решение:
Здесь оба набора данных равномерно сбалансированы около нуля, поэтому среднее значение равно нулю. В первом наборе данных диапазон варьируется приблизительно от -2,5 до 2,5, тогда как во втором наборе данных диапазон варьируется приблизительно от -6 до 6. Нарисуйте диаграмму, как показано ниже: