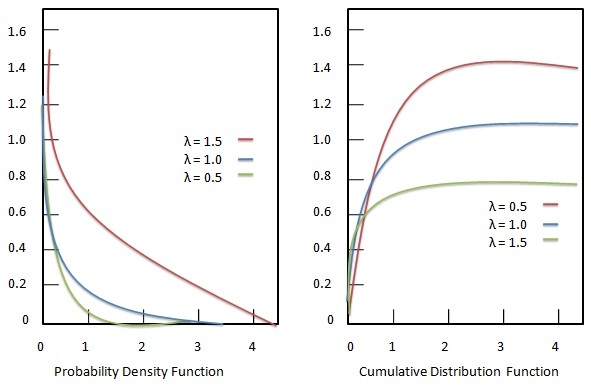
Экспоненциальное распределение или отрицательное экспоненциальное распределение представляет собой распределение вероятностей для описания времени между событиями в пуассоновском процессе. В пуассоновском процессе события происходят непрерывно и независимо с постоянной средней скоростью. Экспоненциальное распределение является частным случаем гамма-распределения.
Функция плотности вероятности
Функция плотности вероятности экспоненциального распределения имеет вид:
формула
f(x; lambda)= \ begin {case} \ lambda e ^ {- \ lambda x}, & \ text {if $ x \ ge 0 $} \\ [7pt] 0, & \ text {if $ x \ lt 0 $} \ end {case}
Где —
-
lambda = параметр скорости.
-
x = случайная величина.
lambda = параметр скорости.
x = случайная величина.
Кумулятивная функция распределения
Накопительная функция экспоненциального распределения имеет вид:
формула
F(x; lambda)= \ begin {case} 1- e ^ {- \ lambda x}, & \ text {if $ x \ ge 0 $} \\ [7pt] 0, & \ text {if $ x \ lt 0 $} \ end {case}
Где —
lambda = параметр скорости.
x = случайная величина.