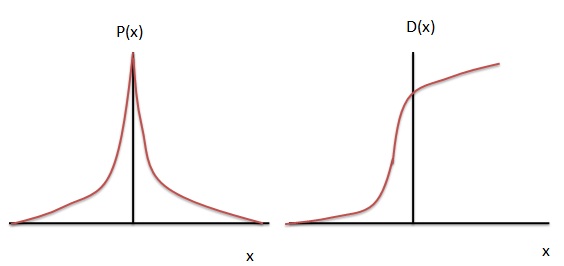
Распределение Лапласа представляет собой распределение различий между двумя независимыми переменными, имеющими идентичные экспоненциальные распределения. Это также называется двойным экспоненциальным распределением.
Функция плотности вероятности
Функция плотности вероятности распределения Лапласа имеет вид:
формула
$ {L (x | \ mu, b) = \ frac {1} {2b} e ^ {- \ frac {| x — \ mu |} {b}}} $
= frac12b \ begin {case} e ^ {- \ frac {x — \ mu} {b}}, & \ text {if $ x \ lt \ mu $} \ \ [7pt] e ^ {- \ frac {\ mu — x} {b}}, & \ text {if $ x \ ge \ mu $} \ end {case}
Где —
-
mu = параметр местоположения.
-
b = параметр масштаба и> 0.
-
x = случайная величина.
mu = параметр местоположения.
b = параметр масштаба и> 0.
x = случайная величина.
Кумулятивная функция распределения
Накопительная функция распределения Лапласа задается как:
формула
D(x)= intx− infty
D(x)= intx− infty
= \ begin {case} \ frac {1} {2} e ^ {\ frac {x — \ mu} {b}}, & \ text {if $ x \ lt \ mu $} \\ [7pt] 1 — \ frac {1} {2} e ^ {- \ frac {x — \ mu} {b}}, & \ text {if $ x \ ge \ mu $} \ end {case}
= frac12+ frac12sgn(x− mu)(1−e− frac|x− mu|b)
Где —
mu = параметр местоположения.
b = параметр масштаба и> 0.
x = случайная величина.