Статистика — круговая перестановка

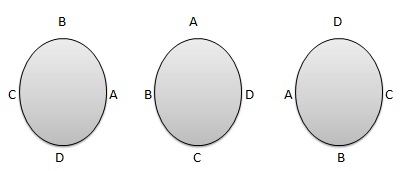
Круговая перестановка — это общее количество способов, которыми n отдельных объектов могут быть расположены вокруг неподвижного круга. Это двух типов.

1. Случай 1: — Порядок по часовой стрелке и против часовой стрелки различен.

2. Случай 2: — По часовой стрелке и против часовой стрелки одинаковые.

Случай 1: — Порядок по часовой стрелке и против часовой стрелки различен.

Случай 2: — По часовой стрелке и против часовой стрелки одинаковые.

Случай 1: Формула

${P_n = (n-1)!}$

Где —

• ${P_n}$ = представляет круговую перестановку

• ${n}$ = Количество объектов

${P_n}$ = представляет круговую перестановку

${n}$ = Количество объектов

Случай 2: Формула

${P_n = \ frac {n-1!} {2!}}$

Где —

• ${P_n}$ = представляет круговую перестановку

• ${n}$ = Количество объектов

${P_n}$ = представляет круговую перестановку

${n}$ = Количество объектов

пример

Постановка задачи:

Рассчитайте круговую перестановку 4 человек, сидящих за круглым столом, учитывая, что i) ордера по часовой стрелке и против часовой стрелки различны и ii) ордера по часовой стрелке и против часовой стрелки одинаковы.

Решение:

В случае 1, n = 4, используя формулу

${P_n = (n-1)!}$

Применить формулу

$ {P_4 = (4-1)! \\ [7pt] \ = 3! \\ [7pt] \ = 6} $

В случае 2 n = 4, используя формулу

${P_n = \ frac {n-1!} {2!}}$

Применить формулу

P4= fracn−1!2![7pt] = frac4−1!2![7pt] = frac3!2![7pt] = frac62[7pt] =3${P_4 = \ frac {n-1!} {2!} \\ [7pt] \ = \ frac {4-1!} {2!} \\ [7pt] \ = \ frac {3!} {2 !} \\ [7pt] \ = \ frac {6} {2} \\ [7pt] \ = 3}$