Статистика — Квадратичное уравнение регрессии

Квадратичная регрессия применяется для определения уравнения параболы, которое может наилучшим образом соответствовать заданному набору данных. Это имеет следующую форму:

${y = ax ^ 2 + bx + c \ where \ a \ ne 0}$

Метод наименьших квадратов можно использовать для определения уравнения квадратичной регрессии. В этом методе мы находим значения a, b и c таким образом, чтобы квадрат вертикального расстояния между каждой данной точкой (${x_i, y_i}$) и уравнением параболы (${y = ax ^ 2 + bx + 2}$) минимально. Матричное уравнение для параболической кривой имеет вид:

Коэффициент корреляции, г

Коэффициент корреляции r определяет, насколько хорошо квадратное уравнение может соответствовать заданным данным. Если r близко к 1, то это хорошо подходит. r можно вычислить по следующей формуле.

r=1− fracSSESST где[7pt] SSE= sum(yi−axi2−bx+i−c)2[7pt] SST= sum(yi− bary)2${r = 1 - \ frac {SSE} {SST} \ где \\ [7pt] \ SSE = \ sum (y_i - a {x_i} ^ 2 - bx + i - c) ^ 2 \\ [7pt] \ SST = \ sum (y_i - \ bar y) ^ 2}$

Как правило, калькуляторы квадратичной регрессии используются для вычисления уравнения квадратичной регрессии.

пример

Постановка задачи:

Вычислить квадратное уравнение регрессии следующих данных. Проверьте его лучший фитнес.

Решение:

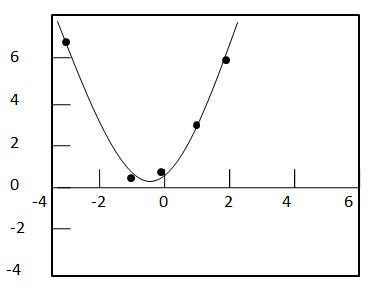
Вычислите квадратичную регрессию на калькуляторе, поместив значения x и y. Наиболее подходящее квадратное уравнение для указанных выше точек имеет вид

${y = 1.1071x ^ 2 + 0.5714x}$

Чтобы проверить лучшую пригодность, постройте график.

Таким образом, значение коэффициента корреляции r для данных составляет 0,99420 и близко к 1. Следовательно, квадратное уравнение регрессии лучше всего подходит.