Статистика теста — это z-оценка (z), определяемая следующим уравнением. z= frac(p−P) sigma, где P — гипотетическое значение доли населения в нулевой гипотезе, p — выборочная доля, а sigma — стандартное отклонение распределения выборки.
Статистика теста определяется и задается следующей функцией:
формула
z= frac hatp−po sqrt fracpo(1−po)n
z= frac hatp−po sqrt fracpo(1−po)n
Где —
-
z = Тестовая статистика
-
n = размер выборки
-
po = нулевое предполагаемое значение
-
hatp = наблюдаемая пропорция
z = Тестовая статистика
n = размер выборки
po = нулевое предполагаемое значение
hatp = наблюдаемая пропорция
пример
Постановка задачи:
Опрос утверждает, что 9 из 10 врачей рекомендуют аспирин для своих пациентов с головной болью. Чтобы проверить это утверждение, была выбрана случайная выборка из 100 врачей. Из этих 100 врачей 82 указывают, что они рекомендуют аспирин. Точно ли это утверждение? Используйте альфа = 0,05.
Решение:
Определить нулевые и альтернативные гипотезы
H0;p=.90[7pt]H0;p ne.90
H0;p=.90[7pt]H0;p ne.90
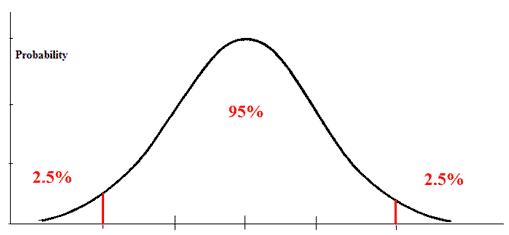
Здесь Альфа = 0,05. Используя альфа 0,05 с двусторонним тестом, мы ожидаем, что наш дистрибутив будет выглядеть примерно так:
Здесь у нас 0,025 в каждом хвосте. Если посмотреть на 1 — 0,025 в нашей z-таблице, мы найдем критическое значение 1,96. Таким образом, наше правило принятия решения для этого двустороннего теста: Если Z меньше -1,96 или больше 1,96, отклоните нулевую гипотезу. Рассчитайте статистику теста:
z= frac hatp−po sqrt fracpo(1−po)n[7pt] hatp=.82[7pt]po=.90[7pt]n=100[7pt]zo= frac.82−.90 sqrt frac.90(1−.90)100[7pt] = frac−.080.03[7pt] =−2.667
z= frac hatp−po sqrt fracpo(1−po)n[7pt] hatp=.82[7pt]po=.90[7pt]n=100[7pt]zo= frac.82−.90 sqrt frac.90(1−.90)100[7pt] = frac−.080.03[7pt] =−2.667
При z = -2,667 Таким образом, в результате мы должны отвергнуть нулевую гипотезу и, как заключение, утверждение, что 9 из 10 врачей рекомендуют аспирин для своих пациентов, не является точным, z = -2,667, р <0,05.