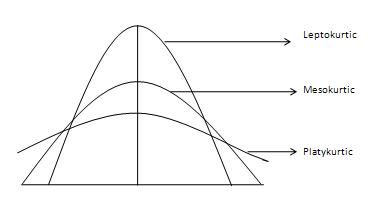
Степень хвостатости распределения измеряется по куртозу. Это говорит нам о том, в какой степени распределение более или менее подвержено выбросам (более тяжелым или легким хвостам), чем нормальное распределение. Три различных типа кривых, любезно предоставленных Investopedia, показаны следующим образом:
Трудно отличить различные типы эксцессов от графиков плотности (левая панель), поскольку хвосты близки к нулю для всех распределений. Но различия в хвостах легко увидеть на обычных графиках квантиль-квантиль (правая панель).
Нормальная кривая называется мезокуртической кривой. Если кривая распределения является более склонной (или более тяжелой), чем нормальная кривая или кривая мезокурта, то она называется кривой Лептокурта. Если кривая менее склонна к внешним воздействиям (или с более легким хвостом), чем нормальная кривая, она называется платикюртической кривой. Куртоз измеряется моментами и определяется по следующей формуле:
формула
beta2= frac mu4 mu2
beta2= frac mu4 mu2
Где —
-
mu4= frac sum(x− barx)4N
mu4= frac sum(x− barx)4N
Чем больше значение \ beta_2, тем более пиковая или лептокуротическая кривая. Нормальная кривая имеет значение 3, у leptokurtic \ beta_2 больше 3, а для platykurtic \ beta_2 меньше 3.
пример
Постановка задачи:
Приведены данные о суточной заработной плате 45 работников завода. Вычислите \ beta_1 и \ beta_2, используя момент о среднем. Прокомментируйте результаты.
| Заработная плата (РТС). | Количество работников |
|---|---|
| 100-200 | 1 |
| 120-200 | 2 |
| 140-200 | 6 |
| 160-200 | 20 |
| 180-200 | 11 |
| 200-200 | 3 |
| 220-200 | 2 |
Решение:
| заработная плата (Rs). |
Количество работников (Е) |
Mid-пт м |
м — гидроразрыва17020 d |
FD | 2FD | 3FD | 4FD |
|---|---|---|---|---|---|---|---|
| 100-200 | 1 | 110 | -3 | -3 | 9 | -27 | 81 |
| 120-200 | 2 | 130 | -2 | -4 | 8 | -16 | 32 |
| 140-200 | 6 | 150 | -1 | -6 | 6 | -6 | 6 |
| 160-200 | 20 | 170 | 0 | 0 | 0 | 0 | 0 |
| 180-200 | 11 | 190 | 1 | 11 | 11 | 11 | 11 |
| 200-200 | 3 | 210 | 2 | 6 | 12 | 24 | 48 |
| 220-200 | 2 | 230 | 3 | 6 | 18 | 54 | 162 |
| N=45 | sumfd=10 | sumfd2=64 | sumfd3=40 | sumfd4=330 |
Поскольку отклонения были взяты из предполагаемого среднего, следовательно, мы сначала вычисляем моменты о произвольном происхождении, а затем моменты о среднем. Моменты о произвольном происхождении ‘170’
Моменты о среднем
Из значения движения относительно среднего мы можем теперь вычислить beta1 и beta2:
Из приведенных выше расчетов можно сделать вывод, что beta1, который измеряет асимметрию, почти равен нулю, что указывает на то, что распределение почти симметрично. beta2, который измеряет эксцесс, имеет значение больше 3, что подразумевает, что распределение является лептокуротическим.