Статистика — Распределение хи-квадрат

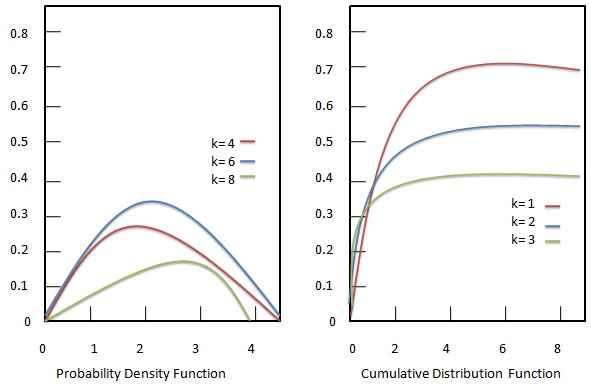
Распределение хи-квадрат (хи-квадрат или ${X ^ 2}$ — распределение) со степенями свободы, k — это распределение суммы квадратов k независимых стандартных нормальных случайных величин. Это одно из наиболее широко используемых распределений вероятностей в статистике. Это частный случай гамма-распределения.

Распределение хи-квадрат широко используется статистиками для вычисления следующего:

• Оценка доверительного интервала для стандартного отклонения популяции нормального распределения с использованием выборочного стандартного отклонения.

• Проверить независимость двух критериев классификации нескольких качественных переменных.

• Чтобы проверить отношения между категориальными переменными.

• Изучить выборочную дисперсию, где основное распределение является нормальным.

• Проверить отклонения различий между ожидаемой и наблюдаемой частотами.

• Провести тест хи-квадрат (проверка на пригодность).

Оценка доверительного интервала для стандартного отклонения популяции нормального распределения с использованием выборочного стандартного отклонения.

Проверить независимость двух критериев классификации нескольких качественных переменных.

Чтобы проверить отношения между категориальными переменными.

Изучить выборочную дисперсию, где основное распределение является нормальным.

Проверить отклонения различий между ожидаемой и наблюдаемой частотами.

Провести тест хи-квадрат (проверка на пригодность).

Функция плотности вероятности

Функция плотности вероятности распределения хи-квадрат задается как:

формула

Где —

• ${\ Gamma (\ frac {k} {2})}$ = Гамма-функция, имеющая значения замкнутой формы для целочисленного параметра k.

• ${x}$ = случайная величина.

• ${k}$ = целочисленный параметр.

${\ Gamma (\ frac {k} {2})}$ = Гамма-функция, имеющая значения замкнутой формы для целочисленного параметра k.

${x}$ = случайная величина.

${k}$ = целочисленный параметр.

Кумулятивная функция распределения

Кумулятивная функция распределения хи-квадрат определяется как:

формула

Где —

${\ gamma (s, t)}$ = неполная нижняя гамма-функция.

${P (s, t)}$ = регуляризованная гамма-функция.

${x}$ = случайная величина.

${k}$ = целочисленный параметр.