Статистика — кумулятивное распределение Пуассона

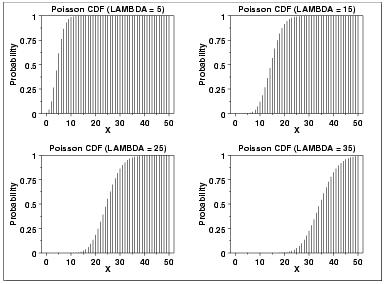
${\ lambda}$ — это параметр формы, который указывает среднее количество событий в данном интервале времени. Ниже приведен график функции плотности вероятности Пуассона для четырех значений ${\ lambda}$. Кумулятивная функция распределения.

формула

$${F (x, \ lambda) = \ sum_ {k = 0} ^ x \ frac {e ^ {- \ lambda} \ lambda ^ x} {k!}}$$

Где —

• ${e}$ = Основание натурального логарифма, равное 2.71828

• ${k}$ = количество вхождений события; вероятность которого определяется функцией.

• ${k!}$ = Факториал k

• ${\ lambda}$ = положительное действительное число, равное ожидаемому числу вхождений в течение данного интервала

${e}$ = Основание натурального логарифма, равное 2.71828

${k}$ = количество вхождений события; вероятность которого определяется функцией.

${k!}$ = Факториал k

${\ lambda}$ = положительное действительное число, равное ожидаемому числу вхождений в течение данного интервала

пример

Постановка задачи:

Сложная программная система усредняет 7 ошибок на 5000 строк кода. Какова вероятность точно 2 ошибки в 5000 строк случайно выбранных строк кода?

Решение:

Вероятность точно 2 ошибки в 5000 строк случайно выбранных строк кода составляет: