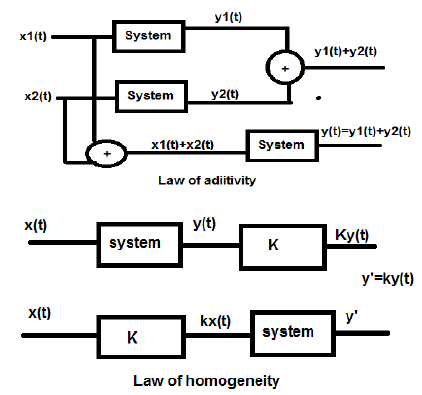
Линейная система подчиняется законам суперпозиции. Этот закон является необходимым и достаточным условием для доказательства линейности системы. Помимо этого, система представляет собой комбинацию двух типов законов —
- Закон аддитивности
- Закон однородности
Как закон гомогенности, так и закон аддитивности показаны на рисунках выше. Однако существуют некоторые другие условия, чтобы проверить, является ли система линейной или нет.
Условия —
- Выход должен быть нулевым для нулевого ввода.
- В системе не должно быть нелинейных операторов.
Примеры нелинейных операторов —
(а) Тригонометрические операторы — Sin, Cos, Tan, Cot, Sec, Cosec и т. д.
(б) экспоненциальный, логарифмический, модуль, квадрат, куб и т. д.
(c) sa (i / p), Sinc (i / p), Sqn (i / p) и т. д.
Ни вход x, ни выход y не должны иметь этих нелинейных операторов.
Примеры
Выясним, являются ли следующие системы линейными.
а) y(t)=x(t)+3
Эта система не является линейной системой, поскольку она нарушает первое условие. Если мы введем ввод как ноль, сделав x (t) = 0, то результат будет не нулевым.
б) y(t)= sintx(t)
В этой системе, если мы дадим входное значение как ноль, выходное значение станет нулевым. Следовательно, первое условие явно выполнено. Опять же, нет нелинейного оператора, который был бы применен к x (t). Следовательно, второе условие также выполнено. Следовательно, система является линейной системой.
в) y(t)= sin(x(t))
В вышеприведенной системе первое условие выполняется, потому что если мы положим x (t) = 0, то на выходе также будет sin (0) = 0. Однако второе условие не выполняется, поскольку существует нелинейный оператор, который работает х (т). Следовательно, система не является линейной.