Предположим, что входная последовательность x (n) большой длительности должна обрабатываться системой, имеющей импульсную характеристику конечной длительности, путем свертки двух последовательностей. Поскольку линейная фильтрация, выполняемая посредством DFT, включает в себя работу с блоком данных фиксированного размера, входная последовательность перед обработкой разделяется на блок данных другого фиксированного размера.
Последовательные блоки затем обрабатываются по одному, и результаты объединяются для получения чистого результата.
Поскольку свертка выполняется путем разделения длинной входной последовательности на секции с разными фиксированными размерами, она называется секционированной сверткой. Длинная входная последовательность сегментируется на блоки фиксированного размера до обработки FIR-фильтра.
Для оценки дискретной свертки используются два метода:
-
Метод перекрытия-сохранения
-
Метод перекрытия-добавления
Метод перекрытия-сохранения
Метод перекрытия-добавления
Метод сохранения с перекрытием
Сохранение с перекрытием — это традиционное название для эффективного способа оценки дискретной свертки между очень длинным сигналом x (n) и фильтром с конечной импульсной характеристикой (FIR) h (n). Ниже приведены шаги метода сохранения перекрытия —
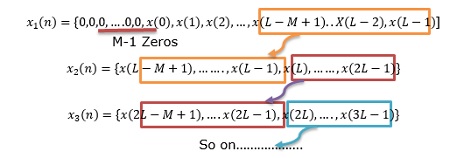
Пусть длина блока входных данных = N = L + M-1. Следовательно, длина DFT и IDFT = N. Каждый блок данных несет точки данных M-1 предыдущего блока, за которыми следует L новых точек данных, чтобы сформировать последовательность данных длины N = L + M-1.
-
Во-первых, N-точечное ДПФ вычисляется для каждого блока данных.
-
При добавлении (L-1) нулей импульсная характеристика КИХ-фильтра увеличивается в длине, а точка DFT вычисляется и сохраняется.
-
Умножение двух N-точечных ДПФ H (k) и X m (k): Y ′ m (k) = H (k) .X m (k), где K = 0,1,2,… N-1
-
Тогда IDFT [Y ′ m ((k)] = y ′ ((n) = [y ′ m (0), y ′ m (1), y ′ m (2), ……. y ‘M (M-1), y’ m (M), ……. y ‘ m (N-1)]
(здесь N-1 = L + M-2)
-
Первые точки M-1 повреждены из-за наложения имен и, следовательно, они отбрасываются, потому что запись данных имеет длину N.
-
Последние L точек в точности совпадают в результате свертки, поэтому
y ‘ m (n) = y m (n), где n = M, M + 1,… .N-1
-
Чтобы избежать наложения, последние элементы M-1 каждой записи данных сохраняются, и эти точки переносятся на следующую запись и становятся первыми элементами M-1.
Во-первых, N-точечное ДПФ вычисляется для каждого блока данных.
При добавлении (L-1) нулей импульсная характеристика КИХ-фильтра увеличивается в длине, а точка DFT вычисляется и сохраняется.
Умножение двух N-точечных ДПФ H (k) и X m (k): Y ′ m (k) = H (k) .X m (k), где K = 0,1,2,… N-1
Тогда IDFT [Y ′ m ((k)] = y ′ ((n) = [y ′ m (0), y ′ m (1), y ′ m (2), ……. y ‘M (M-1), y’ m (M), ……. y ‘ m (N-1)]
(здесь N-1 = L + M-2)
Первые точки M-1 повреждены из-за наложения имен и, следовательно, они отбрасываются, потому что запись данных имеет длину N.
Последние L точек в точности совпадают в результате свертки, поэтому
y ‘ m (n) = y m (n), где n = M, M + 1,… .N-1
Чтобы избежать наложения, последние элементы M-1 каждой записи данных сохраняются, и эти точки переносятся на следующую запись и становятся первыми элементами M-1.
-
Результат IDFT, где избегают первых точек M-1, чтобы аннулировать псевдонимы, а оставшиеся точки L составляют желаемый результат как результат линейной свертки.
Результат IDFT, где избегают первых точек M-1, чтобы аннулировать псевдонимы, а оставшиеся точки L составляют желаемый результат как результат линейной свертки.
Метод добавления перекрытия
Ниже приведены шаги для определения дискретной свертки с использованием метода перекрытия —
Пусть размер входного блока данных равен L. Следовательно, размер DFT и IDFT: N = L + M-1
Каждый блок данных добавляется с нулями M-1 до последнего.
Вычислить N-точку DFT.
Умножаются два N-точечных ДПФ: Y m (k) = H (k) .X m (k), где k = 0, 1,2,…., N-1
IDFT [Y m (k)] создает блоки длиной N, на которые не влияет псевдоним, так как размер DFT равен N = L + M-1 и увеличивает длину последовательностей до N-точек, добавляя нули M-1 к каждому блок.
Последние точки M-1 каждого блока должны перекрываться и добавляться к первым точкам M-1 последующего блока.
(причина: каждый блок данных заканчивается нулями M-1)
Следовательно, этот метод известен как метод наложения-сложения. Таким образом, мы получаем —
y (n) = {y 1 (0), y 1 (1), y 1 (2), … .., y 1 (L-1), y 1 (L) + y 2 (0), y 1 (L + 1) + y 2 (1), … … .., y 1 (N-1) + y 2 (M-1), y 2 (M), … .. … … …}