DSP — Разные сигналы

Есть и другие сигналы, которые являются результатом выполненной над ними операции. Некоторые распространенные типы сигналов обсуждаются ниже.

Сопряженные сигналы

Сигналы, удовлетворяющие условию x(t)=x∗(−t)$x (t) = x * (- t)$, называются сопряженными сигналами.

Пусть x(t)=a(t)+jb(t)$x (t) = a (t) + jb (t)$ … eqn. 1

Итак, x(−t)=a(−t)+jb(−t)$x (-t) = a (-t) + jb (-t)$

И x∗(−t)=a(−t)−jb(−t)$x * (- t) = a (-t) -jb (-t)$ … уравнение 2

По условию x(t)=x∗(−t)$x (t) = x * (- t)$

Если мы сравним оба производных уравнения 1 и 2, мы увидим, что действительная часть четная, а мнимая часть нечетная. Это условие для того, чтобы сигнал был сопряженным типом.

Сопряженные антисимметричные сигналы

Сигналы, которые удовлетворяют условию x(t)=−x∗(−t)$x (t) = -x * (- t)$, называются сопряженным антисимметричным сигналом

Пусть x(t)=a(t)+jb(t)$x (t) = a (t) + jb (t)$ … eqn. 1

Так что x(−t)=a(−t)+jb(−t)$x (-t) = a (-t) + jb (-t)$

И x∗(−t)=a(−t)−jb(−t)$x * (- t) = a (-t) -jb (-t)$

−x∗(−t)=−a(−t)+jb(−t)$-x * (- t) = -a (-t) + jb (-t)$ … уравнение 2

По условию x(t)=−x∗(−t)$x (t) = -x * (- t)$

Теперь снова сравните оба уравнения так же, как мы это делали для сопряженных сигналов. Здесь мы обнаружим, что действительная часть нечетна, а мнимая часть четна. Это условие для того, чтобы сигнал стал сопряженным антисимметричным типом.

пример

Пусть заданный сигнал будет x(t)= sint+jt2$x (t) = \ sin t + jt ^ {2}$.

Здесь действительная часть, являющаяся  sint$\ sin t$, является нечетной, а мнимая часть, являющаяся t2$t ^ 2$, является четной. Таким образом, этот сигнал можно классифицировать как сопряженный антисимметричный сигнал.

Любую функцию можно разделить на две части. Одна часть является сопряженной симметрией, а другая — сопряженной антисимметричной. Таким образом, любой сигнал x (t) может быть записан как

x(t)=xcs(t)+xcas(t)

$$x (t) = xcs (t) + xcas (t)$$

Где xcs(t)$xcs (t)$ — сопряженный симметричный сигнал, а xcas(t)$xcas (t)$ — сопряженный антисимметричный сигнал

xcs(t)= frac[x(t)+x∗(−t)]2

$$xcs (t) = \ frac {[x (t) + x * (- t)]} {2}$$

А также

xcas(t)= frac[x(t)−x∗(−t)]2

$$xcas (t) = \ frac {[x (t) -x * (- t)]} {2}$$

Полуволновые симметричные сигналы

Когда сигнал удовлетворяет условию cx(t)=−x(t pm( fracT02))$cx (t) = -x (t \ pm (\ frac {T_ {0}} {2}))$, он называется полуволновым симметричным сигналом. Здесь изменение амплитуды и сдвиг сигнала по времени происходит наполовину. Для полуволнового симметричного сигнала среднее значение будет равно нулю, но это не тот случай, когда ситуация меняется на противоположную.

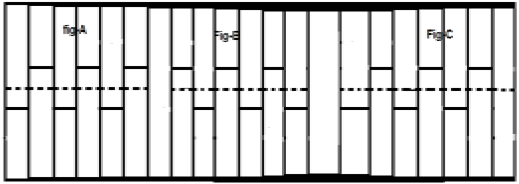
Рассмотрим сигнал x (t), как показано на рисунке A выше. Первый шаг — сдвинуть сигнал по времени и сделать его x[t−( fracT2)]$x [t - (\ frac {T} {2})]$. Таким образом, новый сигнал изменяется, как показано на рисунке B. Далее мы меняем амплитуду сигнала, то есть делаем его −x[t−( fracT2)]$-x [t - (\ frac {T} {2})]$, как показано на рисунке C. Поскольку этот сигнал повторяется после сдвига полупериода и изменения амплитуды, он является полуволновым симметричным сигналом.

Ортогональный сигнал

Два сигнала x (t) и y (t) называются ортогональными, если они удовлетворяют следующим двум условиям.

Условие 1 —  int infty− inftyx(t)y(t)=0$\ int _ {- \ infty} ^ {\ infty} x (t) y (t) = 0$ [для непериодического сигнала]

Условие 2 —  intx(t)y(t)=0$\ int x (t) y (t) = 0$ [Для периодического сигнала]

Сигналы, которые содержат нечетные гармоники (3- ^й , 5- ^й , 7- ^й … и т. Д.) И имеют разные частоты, взаимно ортогональны друг другу.

В сигналах тригонометрического типа функции синуса и косинуса также ортогональны друг другу; при условии, что они имеют одинаковую частоту и находятся в одинаковой фазе. Таким же образом постоянные (сигналы постоянного тока) и синусоидальные сигналы также ортогональны друг другу. Если x (t) и y (t) являются двумя ортогональными сигналами и z(t)=x(t)+y(t)$z (t) = x (t) + y (t)$, то мощность и энергия z (t) можно записать в виде;

P(z)=p(x)+p(y)

$$P (z) = p (x) + p (y)$$ E(z)=E(x)+E(y)

$$E (z) = E (x) + E (y)$$

пример

Проанализируйте сигнал: z(t)=3+4 sin(2 pit+300)$z (t) = 3 + 4 \ sin (2 \ pi t + 30 ^ 0)$

Здесь сигнал содержит сигнал постоянного тока (3) и одну синусоидальную функцию. Таким образом, по свойству этот сигнал является ортогональным сигналом, и два суб-сигнала в нем взаимно ортогональны друг другу.