Сдвиг означает движение сигнала либо во временной области (вокруг оси Y), либо в амплитудной области (вокруг оси X). Соответственно, мы можем классифицировать сдвиг на две категории, названные как сдвиг во времени и сдвиг амплитуды, которые впоследствии обсуждаются ниже.
Временной сдвиг
Сдвиг времени означает сдвиг сигналов во временной области. Математически это можно записать как
x(t) rightarrowy(t+k)
Это значение К может быть положительным или отрицательным. Согласно знаку значения k, у нас есть два типа сдвига, называемых как сдвиг вправо и сдвиг влево.
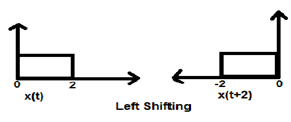
Случай 1 (K> 0)
Когда K больше нуля, смещение сигнала происходит в направлении «влево» во временной области. Следовательно, этот тип сдвига известен как сдвиг влево сигнала.
пример
Случай 2 (К <0)
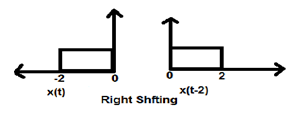
Когда K меньше нуля, смещение сигнала происходит вправо во временной области. Поэтому этот тип смещения известен как смещение вправо.
пример
На приведенном ниже рисунке показано смещение вправо сигнала на 2.
Смещение амплитуды
Сдвиг амплитуды означает смещение сигнала в амплитудной области (вокруг оси X). Математически это можно представить как —
x(t) rightarrowx(t)+K
Это значение К может быть положительным или отрицательным. Соответственно, у нас есть два типа сдвига амплитуды, которые впоследствии обсуждаются ниже.
Случай 1 (K> 0)
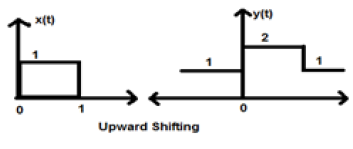
Когда K больше нуля, смещение сигнала происходит вверх по оси x. Поэтому этот тип смещения известен как смещение вверх.
пример
Рассмотрим сигнал x (t), который задается как;
x = \ begin {case} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {case}
Пусть мы взяли K = + 1, поэтому новый сигнал можно записать как —
y(t) rightarrowx(t)+1 Итак, y (t) может быть наконец записано как;
x (t) = \ begin {case} 1, & t <0 \\ 2, & 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {case}
Случай 2 (К <0)
Когда K меньше нуля, происходит смещение сигнала в направлении вниз по оси X. Поэтому это называется смещением сигнала вниз.
пример
Рассмотрим сигнал x (t), который задается как;
x (t) = \ begin {case} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {case}
Пусть мы взяли K = -1, чтобы новый сигнал можно было записать как;
y(t) rightarrowx(t)−1 Итак, y (t) может быть наконец записано как;