DSP — Операции по масштабированию сигналов

Масштабирование сигнала означает, что постоянная умножается на время или амплитуду сигнала.

Масштабирование времени

Если константа умножается на ось времени, она называется масштабированием времени. Это может быть математически представлено как;

$x (t) \ rightarrow y (t) = x (\ alpha t)$ или $x (\ frac {t} {\ alpha})$; где α ≠ 0

Таким образом, если ось Y одинакова, величина оси X уменьшается или увеличивается в зависимости от знака постоянной (положительной или отрицательной). Следовательно, масштабирование также можно разделить на две категории, как описано ниже.

Сжатие времени

Всякий раз, когда альфа больше нуля, амплитуда сигнала делится на альфа, тогда как значение оси Y остается неизменным. Это известно как сжатие времени.

пример

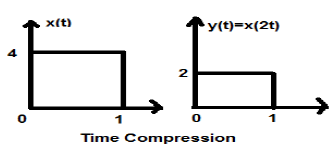
Рассмотрим сигнал x (t), который показан на рисунке ниже. Давайте возьмем значение альфа как 2. Таким образом, y (t) будет x (2t), что проиллюстрировано на данном рисунке.

Ясно, что из приведенных выше рисунков видно, что величина времени по оси y остается неизменной, но амплитуда по оси x уменьшается с 4 до 2. Следовательно, это случай сжатия времени.

Расширение времени

Когда время делится на постоянную альфа, величина сигнала по оси Y умножается на альфа, сохраняя величину оси X такой, какая она есть. Поэтому это называется сигналом расширения времени.

пример

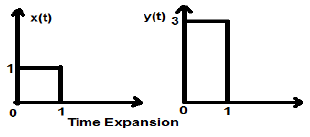
Рассмотрим квадратный сигнал x (t) величиной 1. Когда мы масштабируем его по времени на постоянную 3, такую, что $x (t) \ rightarrow y (t) \ rightarrow x (\ frac {t} {3} )$, то амплитуда сигнала изменяется в 3 раза, что показано на рисунке ниже.

Амплитудное масштабирование

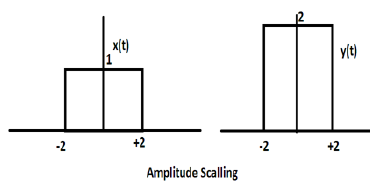
Умножение постоянной на амплитуду сигнала вызывает масштабирование амплитуды. В зависимости от знака константы это может быть либо масштабирование амплитуды, либо ослабление. Рассмотрим прямоугольный сигнал x (t) = Π (t / 4).

Предположим, мы определили другую функцию y (t) = 2 Π (t / 4). В этом случае значение оси Y будет удвоено, сохраняя значение оси времени таким, как оно есть. Это показано на рисунке ниже.

Рассмотрим другую прямоугольную волновую функцию, определенную как z (t), где z (t) = 0,5 Π (t / 4). Здесь амплитуда функции z (t) будет равна половине амплитуды x (t), то есть ось времени, оставаясь неизменной, ось амплитуды будет уменьшена вдвое. Это иллюстрируется рисунком, приведенным ниже.