DSP — Z-Transform Свойства

В этой главе мы поймем основные свойства Z-преобразований.

линейность

В нем говорится, что когда два или более отдельных дискретных сигнала умножаются на константы, их соответствующие Z-преобразования также будут умножаться на одни и те же константы.

Математически,

$$a_1x_1 (n) + a_2x_2 (n) = a_1X_1 (z) + a_2X_2 (z)$$

Доказательство — Мы знаем это,

$$X (Z) = \ sum_ {n = - \ infty} ^ \ infty x (n) Z ^ {- n}$$

$= \ sum_ {n = - \ infty} ^ \ infty (a_1x_1 (n) + a_2x_2 (n)) Z ^ {- n}$

$= a_1 \ sum_ {n = - \ infty} ^ \ infty x_1 (n) Z ^ {- n} + a_2 \ sum_ {n = - \ infty} ^ \ infty x_2 ​​(n) Z ^ {- n}$

$= a_1X_1 (z) + a_2X_2 (z)$ (доказано)

Здесь ROC — это $ROC_1 \ bigcap ROC_2$.

Временной сдвиг

Свойство сдвига во времени показывает, как изменение во временной области в дискретном сигнале повлияет на Z-область, которая может быть записана как;

$$x (n-n_0) \ longleftrightarrow X (Z) Z ^ {- n}$$

Или $x (n-1) \ longleftrightarrow Z ^ {- 1} X (Z)$

Доказательство —

Пусть $y (P) = X (PK)$

$Y (z) = \ sum_ {p = - \ infty} ^ \ infty y (p) Z ^ {- p}$

$= \ sum_ {p = - \ infty} ^ \ infty (x (pk)) Z ^ {- p}$

Пусть s = pk

$= \ sum_ {s = - \ infty} ^ \ infty x (s) Z ^ {- (s + k)}$

$= \ sum_ {s = - \ infty} ^ \ infty x (s) Z ^ {- s} Z ^ {- k}$

$= Z ^ {- k} [\ sum_ {s = - \ infty} ^ \ infty x (m) Z ^ {- s}]$

$= Z ^ {- k} X (Z)$ (доказано)

Здесь ROC может быть записано как Z = 0 (p> 0) или Z = ∞ (p <0)

пример

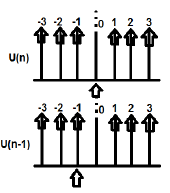
U (n) и U (n-1) могут быть построены следующим образом

Z-преобразование U (n) может быть записано как;

$\ sum_ {n = - \ infty} ^ \ infty [U (n)] Z ^ {- n} = 1$

Z-преобразование U (n-1) может быть записано как;

$\ sum_ {n = - \ infty} ^ \ infty [U (n-1)] Z ^ {- n} = Z ^ {- 1}$

Так что здесь $x (n-n_0) = Z ^ {- n_0} X (Z)$ (доказано)

Масштабирование времени

Свойство Time Scaling сообщает нам, какой будет Z-область сигнала, когда время масштабируется в его дискретной форме, которую можно записать как;

$$a ^ nx (n) \ longleftrightarrow X (a ^ {- 1} Z)$$

Доказательство —

Пусть $y (p) = a ^ {p} x (p)$

$Y (P) = \ sum_ {p = - \ infty} ^ \ infty y (p) Z ^ {- p}$

$= \ sum_ {p = - \ infty} ^ \ infty a ^ px (p) Z ^ {- p}$

$= \ sum_ {p = - \ infty} ^ \ infty x (p) [a ^ {- 1} Z] ^ {- p}$

$= X (a ^ {- 1} Z)$ (следовательно, доказано)

ROC: = Mod (ar1) <Mod (Z) <Mod (ar2), где Mod = Модуль

пример

Определим Z-преобразование $x (n) = a ^ n \ cos \ omega n$, используя свойство масштабирования по времени.

Решение —

Мы уже знаем, что Z-преобразование сигнала $\ cos (\ omega n)$ определяется выражением —

$$\ sum_ {n = - \ infty} ^ \ infty (\ cos \ omega n) Z ^ {- n} = (Z ^ 2-Z \ cos \ omega) / (Z ^ 2-2Z \ cos \ omega +1)$$

Теперь, применяя свойство масштабирования по времени, Z-преобразование $a ^ n \ cos \ omega n$ можно записать в виде;

$\ sum_ {n = - \ infty} ^ \ infty (a ^ n \ cos \ omega n) Z ^ {- n} = X (a ^ {- 1} Z)$

$= [(a ^ {- 1} Z) ^ 2- (a ^ {- 1} Z \ cos \ omega n)] / ((a ^ {- 1} Z) ^ 2-2 (a ^ {- 1} Z \ cos \ omega n) +1)$

$= Z (Za \ cos \ omega) / (Z ^ 2-2az \ cos \ omega + a ^ 2)$

Последовательная дифференциация

Свойство последовательного дифференцирования показывает, что Z-преобразование будет иметь место, когда мы дифференцируем дискретный сигнал во временной области по времени. Это показано ниже.

$$\ frac {dx (n)} {dn} = (1-Z ^ {- 1}) X (Z)$$

Доказательство —

Рассмотрим LHS уравнения — $\ frac {dx (n)} {dn}$

$$= \ frac {[x (n) -x (n-1)]} {[n- (n-1)]}$$

$= x (n) -X (n-1)$

$= x (Z) -Z ^ {- 1} x (Z)$

$= (1-Z ^ {- 1}) x (Z)$ (доказано)

ROC: R1 <Mod (Z) <R2

пример

Найдем Z-преобразование сигнала, заданного как $x (n) = n ^ 2u (n)$

По свойству мы можем написать

$Zz [nU (n)] = -Z \ frac {dZ [U (n)]} {dz}$

$= -Z \ frac {d [\ frac {Z} {Z-1}]} {dZ}$

$= Z / ((Z-1) ^ 2$

$= y (let)$

Теперь Z [ny] можно узнать, снова применив свойство,

$Z (n, y) = -Z \ frac {dy} {dz}$

$= -Z \ frac {d [Z / (Z-1) ^ 3]} {dz}$

$= Z (Z + 1) / (Z-1) ^ 2$

свертка

Это показывает изменение в Z-области системы, когда происходит свертка в форме дискретного сигнала, которая может быть записана как —

$x_1 (n) * x_2 (n) \ longleftrightarrow X_1 (Z) .X_2 (Z)$

Доказательство —

$X (Z) = \ sum_ {n = - \ infty} ^ \ infty x (n) Z ^ {- n}$

$= \ sum_ {n = - \ infty} ^ \ infty [\ sum_ {k = - \ infty} ^ \ infty x_1 (k) x_2 (nk)] Z ^ {- n}$

$= \ sum_ {k = - \ infty} ^ \ infty x_1 (k) [\ sum_n ^ \ infty x_2 ​​(nk) Z ^ {- n}]$

$= \ sum_ {k = - \ infty} ^ \ infty x_1 (k) [\ sum_ {n = - \ infty} ^ \ infty x_2 ​​(nk) Z ^ {- (nk)} Z ^ {- k}]$

Пусть nk = l, тогда приведенное выше уравнение можно записать в виде —

$X (Z) = \ sum_ {k = - \ infty} ^ \ infty x_1 (k) [Z ^ {- k} \ sum_ {l = - \ infty} ^ \ infty x_2 ​​(l) Z ^ {- l }]$

$= \ sum_ {k = - \ infty} ^ \ infty x_1 (k) X_2 (Z) Z ^ {- k}$

$= X_2 (Z) \ sum_ {k = - \ infty} ^ \ infty x_1 (Z) Z ^ {- k}$

$= X_1 (Z) .X_2 (Z)$ (доказано)

ROC: $ROC \ bigcap ROC2$

пример

Найдем свертку, заданную двумя сигналами

$x_1 (n) = \ lbrace 3, -2,2 \ rbrace$ … (уравнение 1)

$x_2 (n) = \ lbrace 2,0 \ leq 4 \ quad и \ quad 0 \ quad elsewhere \ rbrace$ … (уравнение 2)

Z-преобразование первого уравнения можно записать в виде;

$\ sum_ {n = - \ infty} ^ \ infty x_1 (n) Z ^ {- n}$

$= 3-2Z ^ {- 1} + 2Z ^ {- 2}$

Z-преобразование второго сигнала можно записать в виде;

$\ sum_ {n = - \ infty} ^ \ infty x_2 ​​(n) Z ^ {- n}$

$= 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4}$

Итак, свертка двух вышеупомянутых сигналов определяется как —

$X (Z) = [x_1 (Z) ^ * x_2 (Z)]$

$= [3-2Z ^ {- 1} + 2Z ^ {- 2}] \ times [2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4 }]$

$= 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + ... \ quad ... \ quad ...$

Взяв обратное Z-преобразование, мы получим,

$x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace$

Теорема начального значения

Если x (n) является причинной последовательностью, которая имеет свое Z-преобразование как X (z), то теорема о начальном значении может быть записана как;

$X (n) (at \ quad n = 0) = \ lim_ {z \ to \ infty} X (z)$

Доказательство — Мы знаем это,

$X (Z) = \ sum_ {n = 0} ^ \ infty x (n) Z ^ {- n}$

Расширяя вышеприведенные серии, получаем;

$= X (0) Z ^ 0 + X (1) Z ^ {- 1} + X (2) Z ^ {- 2} + ... \ quad ...$

$= X (0) \ times 1 + X (1) Z ^ {- 1} + X (2) Z ^ {- 2} + ... \ quad ...$

В приведенном выше случае, если Z → ∞, то $Z ^ {- n} \ rightarrow 0$ (потому что n> 0)

Поэтому мы можем сказать;

$\ lim_ {z \ to \ infty} X (z) = X (0)$ (доказано)

Окончательная Теорема Значения

Теорема об окончательном значении утверждает, что если Z-преобразование сигнала представлено в виде X (Z) и все полюсы находятся внутри круга, то его окончательное значение обозначается как x (n) или X (∞) и может быть записано как —

$X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {- 1})]]$

Условия —

• Это применимо только для причинных систем.
• В $X (Z) (1-Z ^ {- 1})$ должны быть полюсы внутри единичного круга в Z-плоскости.

Доказательство — мы знаем, что

$Z ^ + [x (n + 1) -x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (n + 1) -x (п)]$

$\ Rightarrow Z ^ + [x (n + 1)] - Z ^ + [x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (п + 1) -x (п)]$

$\ Rightarrow Z [X (Z) ^ + - x (0)] - X (Z) ^ + = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (п + 1) -x (п)]$

Здесь мы можем применить расширенное свойство одностороннего Z-преобразования. Таким образом, вышеприведенное уравнение может быть переписано как;

$Z ^ + [x (n + 1)] = Z [X (2) ^ + - x (0) Z ^ 0] = Z [X (Z) ^ + - x (0)]$

Теперь, положив z = 1 в приведенном выше уравнении, мы можем расширить приведенное выше уравнение —

$\ lim_ {k \ to \ infty} {[x (1) -x (0) + x (6) -x (1) + x (3) -x (2) + ... \ quad ... \ четырехъядерных ... + х (х + 1) -x (к)]}$

Это может быть сформулировано как;

$X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {- 1})]]$ (доказано)

пример

Найдем начальное и конечное значение x (n), сигнал которого определяется

$X (Z) = 2 + 3Z ^ {- 1} + 4Z ^ {- 2}$

Решение — Давайте сначала найдем начальное значение сигнала, применив теорему

$x (0) = \ lim_ {z \ to \ infty} X (Z)$

$= \ lim_ {z \ to \ infty} [2 + 3Z ^ {- 1} + 4Z ^ {- 2}]$

$= 2 + (\ frac {3} {\ infty}) + (\ frac {4} {\ infty}) = 2$

Теперь давайте найдем окончательное значение сигнала, применяя теорему

$x (\ infty) = \ lim_ {z \ to \ infty} [(1-Z ^ {- 1}) X (Z)]$

$= \ lim_ {z \ to \ infty} [(1-Z ^ {- 1}) (2 + 3Z ^ {- 1} + 4Z ^ {- 2})]$

$= \ lim_ {z \ to \ infty} [2 + Z ^ {- 1} + Z ^ {- 2} -4Z ^ {- 3}]$

$= 2 + 1 + 1-4 = 0$

Некоторые другие свойства Z-преобразования перечислены ниже —

Дифференциация по частоте

Это дает изменение в Z-области сигнала, когда его дискретный сигнал дифференцируется по времени.

$nx (n) \ longleftrightarrow -Z \ frac {dX (z)} {dz}$

Его РПЦ можно записать как;

$r_2 &amp;lt;Mod (Z) &amp;lt;r_1$

пример

Найдем значение x (n) через дифференцирование по частоте, дискретный сигнал которого в Z-области задается как $x (n) \ longleftrightarrow X (Z) = log (1 + aZ ^ {- 1})$

По свойству мы можем написать, что

$nx (n) \ longleftrightarrow -Z \ frac {dx (Z)} {dz}$

$= -Z [\ frac {-aZ ^ {- 2}} {1 + aZ ^ {- 1}}]$

$= (aZ ^ {- 1}) / (1 + aZ ^ {- 1})$

$= 1-1 / (1 + aZ ^ {- 1})$

$nx (n) = \ delta (n) - (- a) ^ nu (n)$

$\ Rightarrow x (n) = 1 / n [\ delta (n) - (- a) ^ nu (n)]$

Умножение во времени

Это дает изменение в Z-области сигнала, когда умножение происходит на уровне дискретного сигнала.

$x_1 (n) .x_2 (n) \ longleftrightarrow (\ frac {1} {2 \ Pi j}) [X1 (Z) * X2 (Z)]$

Спряжение во времени

Это изображает представление сопряженного дискретного сигнала в Z-области.

$X ^ * (n) \ longleftrightarrow X ^ * (Z ^ *)$