Такое эффективное использование памяти важно для разработки быстрого оборудования для расчета БПФ. Термин «вычисление на месте» используется для описания этого использования памяти.
Децимация во временной последовательности
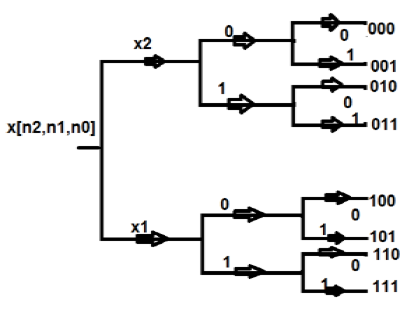
В этой структуре мы представляем все точки в двоичном формате, то есть в 0 и 1. Затем мы обращаем эти структуры в обратном порядке. Последовательность, которую мы получаем после этого, называется последовательностью обращения битов. Это также известно как прореживание во временной последовательности. Расчет на месте восьмиточечного ДПФ показан в табличном формате, как показано ниже —
| ТОЧКИ | БИНАРНЫЙ ФОРМАТ | ВОССТАНОВЛЕНИЕ | ЭКВИВАЛЕНТНЫЕ ТОЧКИ |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Децимация в частотной последовательности
Помимо временной последовательности, N-точечная последовательность также может быть представлена по частоте. Давайте возьмем последовательность из четырех пунктов, чтобы понять это лучше.
Пусть последовательность будет x[0],x[1],x[2],x[3],x[4],x[5],x[6],x[7]. Сначала мы сгруппируем две точки в одну группу. Математически эта последовательность может быть записана как;
x[k]= sumN−1n=0x[n]WnkN
Теперь давайте создадим одну группу с порядковым номером от 0 до 3 и другую группу с последовательностью от 4 до 7. Теперь математически это может быть показано как;
displaystyle sum limit fracN2−1n=0x[n]WnkN+ displaystyle sum limitN−1n=N/2х[п]WпкN
Заменим n на r, где r = 0, 1, 2…. (N / 2-1). Математически,
displaystyle sum limit fracN2−1n=0x[r]WnrN/2
Сначала мы берем первые четыре точки (x [0], x [1], x [2], x [3]) и пытаемся представить их математически следующим образом:
sum3n=0x[n]Wnk8+ sum3n=0x[n+4]W(n+4)k8
= lbrace sum3n=0x[n]+ sum3n=0x[n+4]W(4)k8 rbrace timesWnk8
теперь X[0]= sum3n=0(X[n]+X[n+4])
X[1]= sum3n=0(X[n]+X[n+4])Wnk8
=[X[0]−X[4]+(X[1]−X[5])W18+(X[2]−X[6])W28+(X[3]−X[7])W38
Далее мы можем разбить его на две части, что означает, что вместо того, чтобы разбивать их как последовательность из 4 пунктов, мы можем разбить их на последовательность из 2 пунктов.