Как и непрерывные сигналы времени, сигналы дискретного времени можно классифицировать в соответствии с условиями или операциями над сигналами.
Четные и нечетные сигналы
Четный сигнал
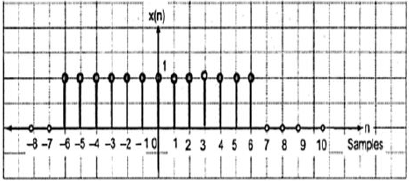
Сигнал называется четным или симметричным, если он удовлетворяет следующему условию;
x(−n)=x(n)
Здесь мы видим, что x (-1) = x (1), x (-2) = x (2) и x (-n) = x (n). Таким образом, это четный сигнал.
Нечетный сигнал
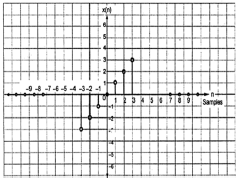
Сигнал называется нечетным, если он удовлетворяет следующему условию;
x(−n)=−x(n)
Из рисунка видно, что x (1) = -x (-1), x (2) = -x (2) и x (n) = -x (-n). Следовательно, это как нечетный, так и антисимметричный сигнал.
Периодические и непериодические сигналы
Дискретный сигнал времени является периодическим тогда и только тогда, когда он удовлетворяет следующему условию:
x(n+N)=x(n)
Здесь сигнал x (n) повторяется после N периода. Это может быть лучше всего понято при рассмотрении сигнала косинуса —
x(n)=A cos(2 pif0n+ theta) x(n+N)=A cos(2 pif0(n+N)+ theta)=A cos(2 pif0n+2 pif0N+ theta) =A cos(2 pif0n+2 pif0N+ тета)
Чтобы сигнал стал периодическим, должно быть выполнено следующее условие;
x(n+N)=x(n) RightarrowA cos(2 pif0n+2 pif0N+ theta)=A cos(2 pif0n+ theta)
т.е. 2 pif0N является целым кратным 2 pi
2 pif0N=2 piK RightarrowN= fracKf0
Частоты дискретных синусоидальных сигналов разделены целым кратным 2 pi.
Сигналы энергии и мощности
Энергетический сигнал
Энергия дискретного сигнала времени обозначается как E. Математически она может быть записана как;
E= displaystyle sum limit+ inftyn=− infty|x(n)|2
Если каждое отдельное значение x(n) возводится в квадрат и складывается, мы получаем сигнал энергии. Здесь x(n) — сигнал энергии, и его энергия конечна во времени, т.е. 0<E< infty
Сигнал силы
Средняя мощность дискретного сигнала представлена как P. Математически это можно записать как;
P= limN to infty frac12N+1 displaystyle sum limit+Nn=−N|x(n)|2
Здесь мощность конечна, т. Е. 0 <P <∞. Однако есть некоторые сигналы, которые не относятся ни к типу энергии, ни к типу сигнала.