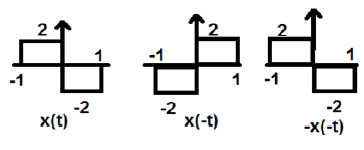DSP — классификация сигналов КТ

Непрерывные сигналы времени могут быть классифицированы в соответствии с различными условиями или операциями, выполняемыми над сигналами.

Четные и нечетные сигналы

Четный сигнал

Сигнал называется даже если он удовлетворяет следующему условию;

$$x (-t) = x (t)$$

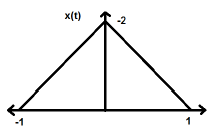
Изменение времени сигнала здесь не подразумевает каких-либо изменений амплитуды. Например, рассмотрим треугольную волну, показанную ниже.

Треугольный сигнал является четным сигналом. Так как он симметричен относительно оси Y. Можно сказать, что это зеркальное отображение относительно оси Y.

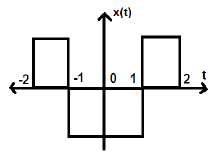
Рассмотрим другой сигнал, как показано на рисунке ниже.

Мы можем видеть, что вышеупомянутый сигнал является четным, поскольку он является симметричным относительно оси Y.

Нечетный сигнал

Сигнал называется нечетным, если он удовлетворяет следующему условию

$$x (-t) = -x (t)$$

Здесь как изменение времени, так и изменение амплитуды происходят одновременно.

На рисунке выше мы видим шаговый сигнал x (t). Чтобы проверить, является ли это нечетным сигналом или нет, сначала мы делаем реверсирование времени, т.е. x (-t), и результат такой, как показано на рисунке. Затем мы инвертируем амплитуду результирующего сигнала, т.е. –x (-t), и получаем результат, как показано на рисунке.

Если мы сравним первый и третий сигналы, мы увидим, что они одинаковы, то есть x (t) = -x (-t), что удовлетворяет нашим критериям. Следовательно, вышеуказанный сигнал является нечетным сигналом.

Некоторые важные результаты, связанные с четными и нечетными сигналами, приведены ниже.

• Даже × Даже = Даже
• Нечетный × Нечетный = Четный
• Четный × Нечетный = Нечетный
• Даже ± даже = даже
• Нечетный ± Нечетный = Нечетный
• Четное ± Нечетное = Ни четное, ни нечетное

Представление любого сигнала в четной или нечетной форме

Некоторые сигналы нельзя напрямую классифицировать на четные или нечетные. Они представлены в виде комбинации четного и нечетного сигнала.

$$x (t) \ rightarrow x_ {e} (t) + x_ {0} (t)$$

Где x _e (t) представляет четный сигнал, а x _o (t) представляет нечетный сигнал

$$X_ {е} (т) = \ гидроразрыва {[х (т) + X (-t)]} {2}$$

А также

$$X_ {0} (т) = \ гидроразрыва {[х (т) -x (-t)]} {2}$$

пример

Найти четные и нечетные части сигнала $x (n) = t + t ^ {2} + t ^ {3}$

Решение — Из обращения x (n) мы получаем

$$x (-n) = -t + t ^ {2} -t ^ {3}$$

Теперь по формуле четная часть

$$x_ {e} (t) = \ frac {x (t) + x (-t)} {2}$$

$$= \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2}$$

$$= t ^ {2}$$

Аналогично, согласно формуле нечетная часть

$$X_ {0} (т) = \ гидроразрыва {[х (т) -x (-t)]} {2}$$

$$= \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3})]} {2}$$

$$= t + t ^ {3}$$

Периодические и непериодические сигналы

Периодические сигналы

Периодический сигнал повторяется через определенный промежуток времени. Мы можем показать это в форме уравнения как —

$$x (t) = x (t) \ pm nT$$

Где n = целое число (1,2,3 ……)

T = основной период времени (FTP) ≠ 0 и ≠ ∞

Фундаментальный период времени (FTP) — это наименьшее положительное и фиксированное значение времени, для которого сигнал является периодическим.

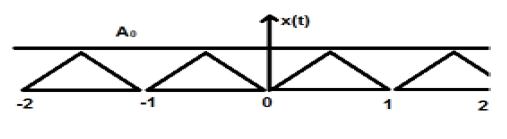
Треугольный сигнал показан на рисунке выше с амплитудой A. Здесь сигнал повторяется через каждые 1 сек. Поэтому можно сказать, что сигнал периодический и его FTP равен 1 секунде.

Непериодический сигнал

Проще говоря, сигналы, которые не являются периодическими, имеют непериодический характер. Как очевидно, эти сигналы не будут повторяться после любого интервала времени.

Непериодические сигналы не следуют определенному формату; следовательно, никакое конкретное математическое уравнение не может их описать.

Сигналы энергии и мощности

Сигнал называется сигналом энергии, если и только если полная содержащаяся энергия конечна и не равна нулю (0 <E <∞). Следовательно, для сигнала любого типа энергии суммарный нормированный сигнал конечен и не равен нулю.

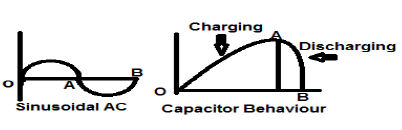
Сигнал синусоидального переменного тока является прекрасным примером сигнала энергетического типа, поскольку в одном случае он находится в положительном полупериоде, а в следующем — в отрицательном. Поэтому его средняя мощность становится равной нулю.

Конденсатор без потерь также является прекрасным примером сигнала энергетического типа, потому что, когда он подключен к источнику, он заряжается до своего оптимального уровня, а когда источник извлекается, он рассеивает такое же количество энергии через нагрузку и делает свою среднюю мощность нуль.

Для любого конечного сигнала x (t) энергия может быть обозначена как E и записана в виде;

$$E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt$$

Спектральная плотность сигналов энергетического типа дает количество энергии, распределенной на различных частотных уровнях.

Тип питания Сигналы

Сигнал называется сигналом типа мощности, если и только если нормализованная средняя мощность является конечной и ненулевой, то есть (0 <p <∞). Для сигнала типа мощности нормализованная средняя мощность конечна и не равна нулю. Почти все периодические сигналы являются сигналами мощности, и их средняя мощность конечна и не равна нулю.

В математической форме мощность сигнала x (t) может быть записана как;

$$P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt$$

Разница между сигналами энергии и мощности

В следующей таблице приведены различия между сигналами энергии и мощности.

Сигнал питания	Энергетический сигнал
Практические периодические сигналы — это сигналы мощности.	Непериодические сигналы являются энергетическими сигналами.
Здесь нормализованная средняя мощность конечна и не равна нулю.	Здесь полная нормированная энергия конечна и не равна нулю.
Математически, $$P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt$$	Математически, $$E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt$$
Наличие этих сигналов бесконечно со временем.	Эти сигналы существуют в течение ограниченного периода времени.
Энергия силового сигнала бесконечна в течение бесконечного времени.	Мощность энергетического сигнала равна нулю в течение бесконечного времени.

Математически,

Математически,

$$E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt$$

Решенные примеры

Пример 1 — Найти мощность сигнала $z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o})$

Решение — Два вышеупомянутых сигнала ортогональны друг другу, потому что их частотные члены идентичны друг другу и имеют одинаковую разность фаз. Таким образом, полная власть будет суммой отдельных полномочий.

Пусть $z (t) = x (t) + y (t)$

Где $x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o})$ и $y (t) = 4 \ sin (3 \ Pi + 30 ^ {o})$

Степень $x (t) = \ frac {2 ^ {2}} {2} = 2$

Степень $y (t) = \ frac {4 ^ {2}} {2} = 8$

Следовательно, $P (z) = p (x) + p (y) = 2 + 8 = 10$ … Ans.

Пример 2 — Проверить, является ли сигнал, заданный $x (t) = t ^ {2} + j \ sin t$, сопряженным или нет?

Решение — Здесь действительная часть, являющаяся t ^2, является четной, а нечетная часть (мнимая), являющаяся $\ sin t$, является нечетной. Таким образом, вышеуказанный сигнал является сопряженным сигналом.

Пример 3. Проверьте, является ли $X (t) = \ sin \ omega t$ нечетным или четным сигналом.

Решение — учитывая $X (t) = \ sin \ omega t$

По времени мы получим $\ sin (- \ omega t)$

Но мы знаем, что $\ sin (- \ phi) = - \ sin \ phi$.

Следовательно,

$$\ sin (- \ omega t) = - \ sin \ omega t$$

Это удовлетворяет условию, чтобы сигнал был нечетным. Следовательно, $\ sin \ omega t$ — нечетный сигнал.