Цифровая обработка сигналов — определение сигналов
Все, что несет информацию, можно назвать сигналом. Он также может быть определен как физическая величина, которая изменяется со временем, температурой, давлением или с любыми независимыми переменными, такими как речевой сигнал или видеосигнал.
Процесс работы, при котором характеристики сигнала (амплитуда, форма, фаза, частота и т. Д.) Претерпевают изменения, называется обработкой сигнала.
Примечание. Любой нежелательный сигнал, мешающий основному сигналу, называется шумом. Таким образом, шум также является сигналом, но нежелательным.
В соответствии с их представлением и обработкой сигналы могут быть классифицированы на различные категории, подробности которых обсуждаются ниже.
Непрерывные сигналы времени
Непрерывные сигналы времени определены вдоль континуума времени и, таким образом, представлены непрерывной независимой переменной. Непрерывные сигналы часто называют аналоговыми сигналами.
Этот тип сигнала показывает непрерывность как по амплитуде, так и по времени. Они будут иметь значения в каждый момент времени. Функции синуса и косинуса являются лучшим примером непрерывного сигнала времени.
Показанный выше сигнал является примером непрерывного сигнала времени, потому что мы можем получить значение сигнала в каждый момент времени.
Сигналы дискретного времени
Сигналы, которые определяются в дискретные моменты времени, называются дискретными сигналами. Следовательно, каждая независимая переменная имеет различное значение. Таким образом, они представлены в виде последовательности чисел.
Хотя речевые и видеосигналы имеют привилегию быть представленными как в непрерывном, так и в дискретном формате времени; при определенных обстоятельствах они идентичны. Амплитуды также показывают дискретные характеристики. Прекрасным примером этого является цифровой сигнал; чья амплитуда и время дискретны.
Рисунок выше изображает дискретную амплитудную характеристику дискретного сигнала за период времени. Математически эти типы сигналов могут быть сформулированы как;
x = \ left \ {x \ left [n \ right] \ right \}, \ quad — \ infty <n <\ infty
Где n — целое число
Это последовательность чисел x, где n- е число в последовательности представлено как x [n].
Цифровая обработка сигналов — основные сигналы КТ
Для тестирования системы, как правило, используются стандартные или основные сигналы. Эти сигналы являются основными строительными блоками для многих сложных сигналов. Следовательно, они играют очень важную роль в изучении сигналов и систем.
Импульс единицы или дельта-функция
Сигнал, удовлетворяющий условию delta(t)= lim epsilon to inftyx(t), называется единичным импульсным сигналом. Этот сигнал стремится к бесконечности, когда t = 0, и стремится к нулю, когда t ≠ 0, так что площадь под его кривой всегда равна единице. Дельта-функция имеет нулевую амплитуду везде excunit_impulse.jpgept при t = 0.
Свойства единичного импульсного сигнала
- δ (t) — четный сигнал.
- δ (t) является примером сигнала ни энергии, ни мощности (NENP).
- Площадь единичного импульсного сигнала может быть записана как;
- Вес или сила сигнала могут быть записаны как;
- Площадь взвешенного импульсного сигнала может быть записана как —
A= int infty− infty delta(t)dt= int infty− infty lim epsilon to0x(t)dt= lim epsilon to0 int infty− infty[x(t)dt]=1
y(t)=A delta(t)
y(t)= int infty− inftyy(t)dt= int infty− inftyA delta(t)=A[ int infty− infty delta(t)dt]=A=1=Wigthedimpulse
Сигнал шага блока
Сигнал, который удовлетворяет следующим двум условиям —
- U(t)=1(когда quadt geq0)и
- U(t)=0(когда quadt<0)
известен как сигнал единичного шага.
Он имеет свойство показывать разрыв при t = 0. В точке разрыва значение сигнала определяется как среднее значение сигнала. Этот сигнал был получен непосредственно до и после точки разрыва (в соответствии с явлениями Гибба).
Если мы добавим шаговый сигнал к другому шаговому сигналу, который масштабируется по времени, то результатом будет единица. Это сигнал типа мощности, и значение мощности составляет 0,5. Среднеквадратическое значение (среднеквадратичное значение) составляет 0,707, а его среднее значение также составляет 0,5.
Пандус Сигнал
Интеграция сигнала шага приводит к сигналу линейного изменения. Он представлен r (t). Сигнал линейного изменения также удовлетворяет условию r(t)= intt− inftyU(t)dt=tU(t). Это не сигнал типа энергии или мощности (NENP).
Параболический Сигнал
Интеграция сигнала Ramp приводит к параболическому сигналу. Он представлен p (t). Параболический сигнал также удовлетворяет условию p(t)= intt− inftyr(t)dt=(t2/2)U(t). Это не сигнал типа энергии или мощности (NENP).
Функция Signum
Эта функция представлена в виде
sgn (t) = \ begin {case} 1 & для \ quad t> 0 \\ — 1 & для \ quad t <0 \ end {case}
Это сигнал типа мощности. Его значения мощности и среднеквадратичные значения (среднеквадратичные) равны 1. Среднее значение функции signum равно нулю.
Sinc Function
Это также функция синуса и записывается как —
SinC(t)= fracSin Pit PiT=Sa( Pit)
Свойства функции Синка
-
Это сигнал типа энергии.
-
Sinc(0)= limt to0 frac sin Pit Pit=1
-
Sinc( infty)= limt to infty frac sin Pi infty Pi infty=0 (диапазон sinπ∞ варьируется от -1 до +1, но все разделено по бесконечности равен нулю)
-
Если sinc(t)=0=> sin Pit=0
Rightarrow Pit=n Pi
Rightarrowt=n(n neq0)
Это сигнал типа энергии.
Sinc(0)= limt to0 frac sin Pit Pit=1
Sinc( infty)= limt to infty frac sin Pi infty Pi infty=0 (диапазон sinπ∞ варьируется от -1 до +1, но все разделено по бесконечности равен нулю)
Если sinc(t)=0=> sin Pit=0
Rightarrow Pit=n Pi
Rightarrowt=n(n neq0)
Синусоидальный сигнал
Сигнал, который является непрерывным по природе, известен как непрерывный сигнал. Общий формат синусоидального сигнала
x(t)=A sin( omegat+ phi)
Вот,
A = амплитуда сигнала
ω = угловая частота сигнала (измеряется в радианах)
φ = фазовый угол сигнала (измеряется в радианах)
Тенденция этого сигнала повторяться через определенный промежуток времени, что называется периодическим сигналом. Период времени сигнала дан как;
T= frac2 pi omega
Схематическое изображение синусоидального сигнала показано ниже.
Прямоугольная функция
Сигнал называется типом прямоугольной функции, если он удовлетворяет следующему условию:
\ pi (\ frac {t} {\ tau}) = \ begin {case} 1, & для \ quad t \ leq \ frac {\ tau} {2} \\ 0, & Иначе \ end {case}
Будучи симметричным относительно оси Y, этот сигнал называется четным сигналом.
Треугольный импульсный сигнал
Любой сигнал, который удовлетворяет следующему условию, называется треугольным сигналом.
\ Delta (\ frac {t} {\ tau}) = \ begin {case} 1 — (\ frac {2 | t |} {\ tau}) & для | t | <\ frac {\ tau} { 2} \\ 0 & для | t |> \ frac {\ tau} {2} \ end {case}
Этот сигнал симметричен относительно оси Y. Следовательно, это также называют четным сигналом.
Цифровая обработка сигналов — базовые сигналы DT
Мы видели, как основные сигналы могут быть представлены в непрерывной временной области. Давайте посмотрим, как основные сигналы могут быть представлены в дискретной временной области.
Последовательность импульсов
Он обозначается как δ (n) в дискретной временной области и может быть определен как;
\ delta (n) = \ begin {case} 1, & для \ quad n = 0 \\ 0, и в противном случае \ end {case}
Сигнал шага блока
Сигнал шага дискретной единицы времени определяется как;
U (n) = \ begin {case} 1, & для \ quad n \ geq0 \\ 0, & для \ quad n <0 \ end {case}
На рисунке выше показано графическое представление дискретной функции шага.
Функция рампы
Дискретная функция линейного изменения может быть определена как —
r (n) = \ begin {case} n, & для \ quad n \ geq0 \\ 0, & для \ quad n <0 \ end {case}
На приведенном выше рисунке показано графическое представление дискретного сигнала линейного изменения.
Параболическая функция
Дискретная единица параболической функции обозначается как p (n) и может быть определена как;
p (n) = \ begin {case} \ frac {n ^ {2}} {2}, & для \ quad n \ geq0 \\ 0, & для \ quad n <0 \ end {case}
С точки зрения функции единичного шага это может быть записано как;
P(n)= fracn22U(n)
На приведенном выше рисунке показано графическое представление параболической последовательности.
Синусоидальный сигнал
Все непрерывные сигналы являются периодическими. Синусоидальные последовательности с дискретным временем могут быть или не быть периодическими. Они зависят от значения ω. Чтобы дискретный сигнал времени был периодическим, угловая частота ω должна быть рациональным кратным 2π.
Дискретный синусоидальный сигнал показан на рисунке выше.
Дискретная форма синусоидального сигнала может быть представлена в формате —
x(n)=A sin( omegan+ phi)
Здесь A, ω и φ имеют свое обычное значение, а n — целое число. Период времени дискретного синусоидального сигнала определяется как —
N= frac2 pim omega
Где N и m — целые числа
DSP — классификация сигналов КТ
Непрерывные сигналы времени могут быть классифицированы в соответствии с различными условиями или операциями, выполняемыми над сигналами.
Четные и нечетные сигналы
Четный сигнал
Сигнал называется даже если он удовлетворяет следующему условию;
x (-t) = x (t)
Изменение времени сигнала здесь не подразумевает каких-либо изменений амплитуды. Например, рассмотрим треугольную волну, показанную ниже.
Треугольный сигнал является четным сигналом. Так как он симметричен относительно оси Y. Можно сказать, что это зеркальное отображение относительно оси Y.
Рассмотрим другой сигнал, как показано на рисунке ниже.
Мы можем видеть, что вышеупомянутый сигнал является четным, поскольку он является симметричным относительно оси Y.
Нечетный сигнал
Сигнал называется нечетным, если он удовлетворяет следующему условию
x (-t) = -x (t)
Здесь как изменение времени, так и изменение амплитуды происходят одновременно.
На рисунке выше мы видим шаговый сигнал x (t). Чтобы проверить, является ли это нечетным сигналом или нет, сначала мы делаем реверсирование времени, т.е. x (-t), и результат такой, как показано на рисунке. Затем мы инвертируем амплитуду результирующего сигнала, т.е. –x (-t), и получаем результат, как показано на рисунке.
Если мы сравним первый и третий сигналы, мы увидим, что они одинаковы, то есть x (t) = -x (-t), что удовлетворяет нашим критериям. Следовательно, вышеуказанный сигнал является нечетным сигналом.
Некоторые важные результаты, связанные с четными и нечетными сигналами, приведены ниже.
- Даже × Даже = Даже
- Нечетный × Нечетный = Четный
- Четный × Нечетный = Нечетный
- Даже ± даже = даже
- Нечетный ± Нечетный = Нечетный
- Четное ± Нечетное = Ни четное, ни нечетное
Представление любого сигнала в четной или нечетной форме
Некоторые сигналы нельзя напрямую классифицировать на четные или нечетные. Они представлены в виде комбинации четного и нечетного сигнала.
x (t) \ rightarrow x_ {e} (t) + x_ {0} (t)
Где x e (t) представляет четный сигнал, а x o (t) представляет нечетный сигнал
X_ {е} (т) = \ гидроразрыва {[х (т) + X (-t)]} {2}
А также
X_ {0} (т) = \ гидроразрыва {[х (т) -x (-t)]} {2}
пример
Найти четные и нечетные части сигнала x (n) = t + t ^ {2} + t ^ {3}
Решение — Из обращения x (n) мы получаем
x (-n) = -t + t ^ {2} -t ^ {3}
Теперь по формуле четная часть
x_ {e} (t) = \ frac {x (t) + x (-t)} {2}
= \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2}
= t ^ {2}
Аналогично, согласно формуле нечетная часть
X_ {0} (т) = \ гидроразрыва {[х (т) -x (-t)]} {2}
= \ frac {[(t + t ^ {2} + t ^ {3}) — (- t + t ^ {2} -t ^ {3})]} {2}
= t + t ^ {3}
Периодические и непериодические сигналы
Периодические сигналы
Периодический сигнал повторяется через определенный промежуток времени. Мы можем показать это в форме уравнения как —
x (t) = x (t) \ pm nT
Где n = целое число (1,2,3 ……)
T = основной период времени (FTP) ≠ 0 и ≠ ∞
Фундаментальный период времени (FTP) — это наименьшее положительное и фиксированное значение времени, для которого сигнал является периодическим.
Треугольный сигнал показан на рисунке выше с амплитудой A. Здесь сигнал повторяется через каждые 1 сек. Поэтому можно сказать, что сигнал периодический и его FTP равен 1 секунде.
Непериодический сигнал
Проще говоря, сигналы, которые не являются периодическими, имеют непериодический характер. Как очевидно, эти сигналы не будут повторяться после любого интервала времени.
Непериодические сигналы не следуют определенному формату; следовательно, никакое конкретное математическое уравнение не может их описать.
Сигналы энергии и мощности
Сигнал называется сигналом энергии, если и только если полная содержащаяся энергия конечна и не равна нулю (0 <E <∞). Следовательно, для сигнала любого типа энергии суммарный нормированный сигнал конечен и не равен нулю.
Сигнал синусоидального переменного тока является прекрасным примером сигнала энергетического типа, поскольку в одном случае он находится в положительном полупериоде, а в следующем — в отрицательном. Поэтому его средняя мощность становится равной нулю.
Конденсатор без потерь также является прекрасным примером сигнала энергетического типа, потому что, когда он подключен к источнику, он заряжается до своего оптимального уровня, а когда источник извлекается, он рассеивает такое же количество энергии через нагрузку и делает свою среднюю мощность нуль.
Для любого конечного сигнала x (t) энергия может быть обозначена как E и записана в виде;
E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt
Спектральная плотность сигналов энергетического типа дает количество энергии, распределенной на различных частотных уровнях.
Тип питания Сигналы
Сигнал называется сигналом типа мощности, если и только если нормализованная средняя мощность является конечной и ненулевой, то есть (0 <p <∞). Для сигнала типа мощности нормализованная средняя мощность конечна и не равна нулю. Почти все периодические сигналы являются сигналами мощности, и их средняя мощность конечна и не равна нулю.
В математической форме мощность сигнала x (t) может быть записана как;
P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt
Разница между сигналами энергии и мощности
В следующей таблице приведены различия между сигналами энергии и мощности.
| Сигнал питания | Энергетический сигнал |
|---|---|
| Практические периодические сигналы — это сигналы мощности. | Непериодические сигналы являются энергетическими сигналами. |
| Здесь нормализованная средняя мощность конечна и не равна нулю. | Здесь полная нормированная энергия конечна и не равна нулю. |
|
Математически, P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt |
Математически, E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt |
| Наличие этих сигналов бесконечно со временем. | Эти сигналы существуют в течение ограниченного периода времени. |
| Энергия силового сигнала бесконечна в течение бесконечного времени. | Мощность энергетического сигнала равна нулю в течение бесконечного времени. |
Математически,
Математически,
E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt
Решенные примеры
Пример 1 — Найти мощность сигнала z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o})
Решение — Два вышеупомянутых сигнала ортогональны друг другу, потому что их частотные члены идентичны друг другу и имеют одинаковую разность фаз. Таким образом, полная власть будет суммой отдельных полномочий.
Пусть z (t) = x (t) + y (t)
Где x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) и y (t) = 4 \ sin (3 \ Pi + 30 ^ {o})
Степень x (t) = \ frac {2 ^ {2}} {2} = 2
Степень y (t) = \ frac {4 ^ {2}} {2} = 8
Следовательно, P (z) = p (x) + p (y) = 2 + 8 = 10 … Ans.
Пример 2 — Проверить, является ли сигнал, заданный x (t) = t ^ {2} + j \ sin t , сопряженным или нет?
Решение — Здесь действительная часть, являющаяся t 2, является четной, а нечетная часть (мнимая), являющаяся \ sin t , является нечетной. Таким образом, вышеуказанный сигнал является сопряженным сигналом.
Пример 3. Проверьте, является ли X (t) = \ sin \ omega t нечетным или четным сигналом.
Решение — учитывая X (t) = \ sin \ omega t
По времени мы получим \ sin (- \ omega t)
Но мы знаем, что \ sin (- \ phi) = — \ sin \ phi .
Следовательно,
\ sin (- \ omega t) = — \ sin \ omega t
Это удовлетворяет условию, чтобы сигнал был нечетным. Следовательно, \ sin \ omega t — нечетный сигнал.
DSP — классификация сигналов DT
Как и непрерывные сигналы времени, сигналы дискретного времени можно классифицировать в соответствии с условиями или операциями над сигналами.
Четные и нечетные сигналы
Четный сигнал
Сигнал называется четным или симметричным, если он удовлетворяет следующему условию;
x (-n) = x (n)
Здесь мы видим, что x (-1) = x (1), x (-2) = x (2) и x (-n) = x (n). Таким образом, это четный сигнал.
Нечетный сигнал
Сигнал называется нечетным, если он удовлетворяет следующему условию;
x (-n) = -x (n)
Из рисунка видно, что x (1) = -x (-1), x (2) = -x (2) и x (n) = -x (-n). Следовательно, это как нечетный, так и антисимметричный сигнал.
Периодические и непериодические сигналы
Дискретный сигнал времени является периодическим тогда и только тогда, когда он удовлетворяет следующему условию:
x (n + N) = x (n)
Здесь сигнал x (n) повторяется после N периода. Это может быть лучше всего понято при рассмотрении сигнала косинуса —
x (n) = A \ cos (2 \ pi f_ {0} n + \ theta) x (n + N) = A \ cos (2 \ pi f_ {0} (n + N) + \ theta) = A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) = A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ тета)
Чтобы сигнал стал периодическим, должно быть выполнено следующее условие;
x (n + N) = x (n) \ Rightarrow A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) = A \ cos (2 \ pi f_ {0} n + \ theta)
т.е. 2 \ pi f_ {0} N является целым кратным 2 \ pi
2 \ pi f_ {0} N = 2 \ pi K \ Rightarrow N = \ frac {K} {f_ {0}}
Частоты дискретных синусоидальных сигналов разделены целым кратным 2 \ pi .
Сигналы энергии и мощности
Энергетический сигнал
Энергия дискретного сигнала времени обозначается как E. Математически она может быть записана как;
E = \ displaystyle \ sum \ limit_ {n = — \ infty} ^ {+ \ infty} | x (n) | ^ 2
Если каждое отдельное значение x (n) возводится в квадрат и складывается, мы получаем сигнал энергии. Здесь x (n) — сигнал энергии, и его энергия конечна во времени, т.е. 0 <E <\ infty
Сигнал силы
Средняя мощность дискретного сигнала представлена как P. Математически это можно записать как;
P = \ lim_ {N \ to \ infty} \ frac {1} {2N + 1} \ displaystyle \ sum \ limit_ {n = -N} ^ {+ N} | x (n) | ^ 2
Здесь мощность конечна, т. Е. 0 <P <∞. Однако есть некоторые сигналы, которые не относятся ни к типу энергии, ни к типу сигнала.
DSP — Разные сигналы
Есть и другие сигналы, которые являются результатом выполненной над ними операции. Некоторые распространенные типы сигналов обсуждаются ниже.
Сопряженные сигналы
Сигналы, удовлетворяющие условию x (t) = x * (- t) , называются сопряженными сигналами.
Пусть x (t) = a (t) + jb (t) … eqn. 1
Итак, x (-t) = a (-t) + jb (-t)
И x * (- t) = a (-t) -jb (-t) … уравнение 2
По условию x (t) = x * (- t)
Если мы сравним оба производных уравнения 1 и 2, мы увидим, что действительная часть четная, а мнимая часть нечетная. Это условие для того, чтобы сигнал был сопряженным типом.
Сопряженные антисимметричные сигналы
Сигналы, которые удовлетворяют условию x (t) = -x * (- t) , называются сопряженным антисимметричным сигналом
Пусть x (t) = a (t) + jb (t) … eqn. 1
Так что x (-t) = a (-t) + jb (-t)
И x * (- t) = a (-t) -jb (-t)
-x * (- t) = -a (-t) + jb (-t) … уравнение 2
По условию x (t) = -x * (- t)
Теперь снова сравните оба уравнения так же, как мы это делали для сопряженных сигналов. Здесь мы обнаружим, что действительная часть нечетна, а мнимая часть четна. Это условие для того, чтобы сигнал стал сопряженным антисимметричным типом.
пример
Пусть заданный сигнал будет x (t) = \ sin t + jt ^ {2} .
Здесь действительная часть, являющаяся \ sin t , является нечетной, а мнимая часть, являющаяся t ^ 2 , является четной. Таким образом, этот сигнал можно классифицировать как сопряженный антисимметричный сигнал.
Любую функцию можно разделить на две части. Одна часть является сопряженной симметрией, а другая — сопряженной антисимметричной. Таким образом, любой сигнал x (t) может быть записан как
x (t) = xcs (t) + xcas (t)
Где xcs (t) — сопряженный симметричный сигнал, а xcas (t) — сопряженный антисимметричный сигнал
xcs (t) = \ frac {[x (t) + x * (- t)]} {2}
А также
xcas (t) = \ frac {[x (t) -x * (- t)]} {2}
Полуволновые симметричные сигналы
Когда сигнал удовлетворяет условию cx (t) = -x (t \ pm (\ frac {T_ {0}} {2})) , он называется полуволновым симметричным сигналом. Здесь изменение амплитуды и сдвиг сигнала по времени происходит наполовину. Для полуволнового симметричного сигнала среднее значение будет равно нулю, но это не тот случай, когда ситуация меняется на противоположную.
Рассмотрим сигнал x (t), как показано на рисунке A выше. Первый шаг — сдвинуть сигнал по времени и сделать его x [t — (\ frac {T} {2})] . Таким образом, новый сигнал изменяется, как показано на рисунке B. Далее мы меняем амплитуду сигнала, то есть делаем его -x [t — (\ frac {T} {2})] , как показано на рисунке C. Поскольку этот сигнал повторяется после сдвига полупериода и изменения амплитуды, он является полуволновым симметричным сигналом.
Ортогональный сигнал
Два сигнала x (t) и y (t) называются ортогональными, если они удовлетворяют следующим двум условиям.
Условие 1 — \ int _ {- \ infty} ^ {\ infty} x (t) y (t) = 0 [для непериодического сигнала]
Условие 2 — \ int x (t) y (t) = 0 [Для периодического сигнала]
Сигналы, которые содержат нечетные гармоники (3- й , 5- й , 7- й … и т. Д.) И имеют разные частоты, взаимно ортогональны друг другу.
В сигналах тригонометрического типа функции синуса и косинуса также ортогональны друг другу; при условии, что они имеют одинаковую частоту и находятся в одинаковой фазе. Таким же образом постоянные (сигналы постоянного тока) и синусоидальные сигналы также ортогональны друг другу. Если x (t) и y (t) являются двумя ортогональными сигналами и z (t) = x (t) + y (t) , то мощность и энергия z (t) можно записать в виде;
P (z) = p (x) + p (y) E (z) = E (x) + E (y)
пример
Проанализируйте сигнал: z (t) = 3 + 4 \ sin (2 \ pi t + 30 ^ 0)
Здесь сигнал содержит сигнал постоянного тока (3) и одну синусоидальную функцию. Таким образом, по свойству этот сигнал является ортогональным сигналом, и два суб-сигнала в нем взаимно ортогональны друг другу.
DSP — Операции по смещению сигналов
Сдвиг означает движение сигнала либо во временной области (вокруг оси Y), либо в амплитудной области (вокруг оси X). Соответственно, мы можем классифицировать сдвиг на две категории, названные как сдвиг во времени и сдвиг амплитуды, которые впоследствии обсуждаются ниже.
Временной сдвиг
Сдвиг времени означает сдвиг сигналов во временной области. Математически это можно записать как
x (t) \ rightarrow y (t + k)
Это значение К может быть положительным или отрицательным. Согласно знаку значения k, у нас есть два типа сдвига, называемых как сдвиг вправо и сдвиг влево.
Случай 1 (K> 0)
Когда K больше нуля, смещение сигнала происходит в направлении «влево» во временной области. Следовательно, этот тип сдвига известен как сдвиг влево сигнала.
пример
Случай 2 (К <0)
Когда K меньше нуля, смещение сигнала происходит вправо во временной области. Поэтому этот тип смещения известен как смещение вправо.
пример
На приведенном ниже рисунке показано смещение вправо сигнала на 2.
Смещение амплитуды
Сдвиг амплитуды означает смещение сигнала в амплитудной области (вокруг оси X). Математически это можно представить как —
x (t) \ rightarrow x (t) + K
Это значение К может быть положительным или отрицательным. Соответственно, у нас есть два типа сдвига амплитуды, которые впоследствии обсуждаются ниже.
Случай 1 (K> 0)
Когда K больше нуля, смещение сигнала происходит вверх по оси x. Поэтому этот тип смещения известен как смещение вверх.
пример
Рассмотрим сигнал x (t), который задается как;
x = \ begin {case} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {case}
Пусть мы взяли K = + 1, поэтому новый сигнал можно записать как —
y (t) \ rightarrow x (t) + 1 Итак, y (t) может быть наконец записано как;
x (t) = \ begin {case} 1, & t <0 \\ 2, & 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {case}
Случай 2 (К <0)
Когда K меньше нуля, происходит смещение сигнала в направлении вниз по оси X. Поэтому это называется смещением сигнала вниз.
пример
Рассмотрим сигнал x (t), который задается как;
x (t) = \ begin {case} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {case}
Пусть мы взяли K = -1, чтобы новый сигнал можно было записать как;
y (t) \ rightarrow x (t) -1 Итак, y (t) может быть наконец записано как;
y (t) = \ begin {case} -1, & t <0 \\ 0, & 0 \ leq t \ leq 2 \\ -1, & t> 0 \ end {case}
DSP — Операции по масштабированию сигналов
Масштабирование сигнала означает, что постоянная умножается на время или амплитуду сигнала.
Масштабирование времени
Если константа умножается на ось времени, она называется масштабированием времени. Это может быть математически представлено как;
x (t) \ rightarrow y (t) = x (\ alpha t) или x (\ frac {t} {\ alpha}) ; где α ≠ 0
Таким образом, если ось Y одинакова, величина оси X уменьшается или увеличивается в зависимости от знака постоянной (положительной или отрицательной). Следовательно, масштабирование также можно разделить на две категории, как описано ниже.
Сжатие времени
Всякий раз, когда альфа больше нуля, амплитуда сигнала делится на альфа, тогда как значение оси Y остается неизменным. Это известно как сжатие времени.
пример
Рассмотрим сигнал x (t), который показан на рисунке ниже. Давайте возьмем значение альфа как 2. Таким образом, y (t) будет x (2t), что проиллюстрировано на данном рисунке.
Ясно, что из приведенных выше рисунков видно, что величина времени по оси y остается неизменной, но амплитуда по оси x уменьшается с 4 до 2. Следовательно, это случай сжатия времени.
Расширение времени
Когда время делится на постоянную альфа, величина сигнала по оси Y умножается на альфа, сохраняя величину оси X такой, какая она есть. Поэтому это называется сигналом расширения времени.
пример
Рассмотрим квадратный сигнал x (t) величиной 1. Когда мы масштабируем его по времени на постоянную 3, такую, что x (t) \ rightarrow y (t) \ rightarrow x (\ frac {t} {3} ) , то амплитуда сигнала изменяется в 3 раза, что показано на рисунке ниже.
Амплитудное масштабирование
Умножение постоянной на амплитуду сигнала вызывает масштабирование амплитуды. В зависимости от знака константы это может быть либо масштабирование амплитуды, либо ослабление. Рассмотрим прямоугольный сигнал x (t) = Π (t / 4).
Предположим, мы определили другую функцию y (t) = 2 Π (t / 4). В этом случае значение оси Y будет удвоено, сохраняя значение оси времени таким, как оно есть. Это показано на рисунке ниже.
Рассмотрим другую прямоугольную волновую функцию, определенную как z (t), где z (t) = 0,5 Π (t / 4). Здесь амплитуда функции z (t) будет равна половине амплитуды x (t), то есть ось времени, оставаясь неизменной, ось амплитуды будет уменьшена вдвое. Это иллюстрируется рисунком, приведенным ниже.
DSP — Операции по обращению сигналов
Всякий раз, когда время в сигнале умножается на -1, сигнал переворачивается. Он создает свое зеркальное отображение вокруг оси Y или X. Это известно как реверсирование сигнала.
Обращение может быть классифицировано на два типа в зависимости от того, умножено ли время или амплитуда сигнала на -1.
Обратное время
Всякий раз, когда время сигнала умножается на -1, оно называется обращением времени сигнала. В этом случае сигнал выдает свое зеркальное отображение вокруг оси Y. Математически это можно записать так:
x (t) \ rightarrow y (t) \ rightarrow x (-t)
Это лучше всего понять на следующем примере.
В приведенном выше примере мы ясно видим, что сигнал был повернут вокруг своей оси Y. Таким образом, это также один из видов масштабирования времени, но здесь величина масштабирования всегда равна (-1).
Обращение амплитуды
Всякий раз, когда амплитуда сигнала умножается на -1, это называется инверсией амплитуды. В этом случае сигнал выдает свое зеркальное отображение вокруг оси X. Математически это можно записать так:
x (t) \ rightarrow y (t) \ rightarrow -x (t)
Рассмотрим следующий пример. Обращение амплитуды видно четко.
DSP — Операции по разграничению сигналов
Две очень важные операции, выполняемые с сигналами, это Дифференциация и Интеграция.
дифференцирование
Дифференциация любого сигнала x (t) означает представление наклона этого сигнала относительно времени. Математически это представляется как;
x (t) \ rightarrow \ frac {dx (t)} {dt}
В случае дифференциации OPAMP эта методология очень полезна. Мы можем легко дифференцировать сигнал графически, а не по формуле. Однако условие состоит в том, что сигнал должен быть прямоугольного или треугольного типа, что происходит в большинстве случаев.
| Оригинальный сигнал | Дифференцированный сигнал |
|---|---|
| Ramp | шаг |
| шаг | Импульс |
| Импульс | 1 |
Таблица выше иллюстрирует состояние сигнала после дифференциации. Например, сигнал линейного изменения преобразуется в сигнал шага после дифференцирования. Аналогично, сигнал единичного шага становится импульсным сигналом.
пример
Пусть данный нам сигнал равен x (t) = 4 [r (t) -r (t-2)] . Когда этот сигнал нанесен, он будет выглядеть так, как показано на рисунке слева. Теперь наша цель — дифференцировать данный сигнал.
Для начала, мы начнем дифференцировать данное уравнение. Мы знаем, что сигнал линейного изменения после дифференцирования дает сигнал единичного шага.
Таким образом, наш результирующий сигнал y (t) может быть записан как;
y (t) = \ frac {dx (t)} {dt}
= \ frac {d4 [r (t) -r (t-2)]} {dt}
= 4 [u (t) -u (t-2)]
Теперь этот сигнал выводится окончательно, что показано в правой части рисунка выше.
DSP — Операции по интеграции сигналов
Интеграция любого сигнала означает суммирование этого сигнала в определенной временной области для получения модифицированного сигнала. Математически это можно представить как —
x (t) \ rightarrow y (t) = \ int _ {- \ infty} ^ {t} x (t) dt
Здесь также, в большинстве случаев, мы можем выполнить математическое интегрирование и найти полученный сигнал, но прямое интегрирование в быстрой последовательности возможно для сигналов, которые графически представлены в прямоугольном формате. Как и дифференцирование, здесь мы также будем ссылаться на таблицу, чтобы быстро получить результат.
| Оригинальный сигнал | Интегрированный сигнал |
|---|---|
| 1 | импульс |
| Импульс | шаг |
| шаг | Ramp |
пример
Рассмотрим сигнал x (t) = u (t) -u (t-3) . Это показано на фиг.1-1 ниже. Ясно, что мы видим, что это шаговый сигнал. Теперь мы интегрируем это. Обращаясь к таблице, мы знаем, что интегрирование сигнала шага дает сигнал линейного изменения.
Тем не менее, мы рассчитаем это математически,
y (t) = \ int _ {- \ infty} ^ {t} x (t) dt
= \ int _ {- \ infty} ^ {t} [u (t) -u (t-3)] dt
= \ int _ {- \ infty} ^ {t} u (t) dt- \ int _ {- \ infty} ^ {t} u (t-3) dt
= r (t) -r (t-3)
То же самое, как показано на рис-2,
DSP — Операции по свертке сигналов
Свертка двух сигналов во временной области эквивалентна умножению их представления в частотной области. Математически мы можем записать свертку двух сигналов как
y (t) = x_ {1} (t) * x_ {2} (t) = \ int _ {- \ infty} ^ {\ infty} x_ {1} (p) .x_ {2 } (ф) дп
Шаги для свертки
- Возьмите сигнал x 1 (t) и поместите туда t = p так, чтобы он был x 1 (p).
- Возьмите сигнал x 2 (t) и сделайте шаг 1 и сделайте его x 2 (p).
- Сделайте сворачивание сигнала, т.е. х 2 (-p).
- Выполните сдвиг во времени вышеуказанного сигнала x 2 [- (pt)]
- Затем сделайте умножение обоих сигналов. то есть x_ {1} (p) .x_ {2} [- (p − t)]
пример
Сделаем свертку ступенчатого сигнала u (t) с его собственным видом.
y (t) = u (t) * u (t)
= \ int _ {- \ infty} ^ {\ infty} [u (p) .u [- (pt)] dp
Теперь это t может быть больше или меньше нуля, что показано на рисунках ниже
Таким образом, в приведенном выше случае, результат возникает со следующими возможностями
y (t) = \ begin {case} 0, & if \ quad t <0 \\\ int_ {0} ^ {t} 1dt, & for \ quad t> 0 \ end {case}
= \ begin {case} 0, & если \ quad t <0 \\ t, & t> 0 \ end {case} = r (t)
Свойства свертки
Коммутативный
В нем говорится, что порядок свертки не имеет значения, что может быть математически показано как
x_ {1} (t) * x_ {2} (t) = x_ {2} (t) * x_ {1} (t)
ассоциативный
В нем говорится, что порядок свертки, включающий три сигнала, может быть любым. Математически это может быть показано как;
x_ {1} (t) * [x_ {2} (t) * x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t)] * x_ {3} (т)
дистрибутивный
Сначала могут быть добавлены два сигнала, а затем их свертка может быть сделана с третьим сигналом. Это эквивалентно свертке двух сигналов по отдельности с третьим сигналом и добавлению окончательно. Математически это можно записать так:
x_ {1} (t) * [x_ {2} (t) + x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t) + x_ {1} ( т) * X_ {3} (т)]
Площадь
Если сигнал является результатом свертки двух сигналов, то область сигнала — это умножение этих отдельных сигналов. Математически это можно записать
Если y (t) = x_ {1} * x_ {2} (t)
Тогда, Площадь у (т) = Площадь х 1 (т) Х Площадь х 2 (т)
пересчет
Если два сигнала масштабируются до некоторой неизвестной постоянной «а» и свертка выполняется, то результирующий сигнал также будет свернут в одну и ту же постоянную «а» и будет разделен на эту величину, как показано ниже.
Если x_ {1} (t) * x_ {2} (t) = y (t)
Тогда x_ {1} (at) * x_ {2} (at) = \ frac {y (at)} {a}, a \ ne 0
задержка
Предположим, что сигнал y (t) является результатом свертки двух сигналов x1 (t) и x2 (t). Если два сигнала задерживаются на время t1 и t2 соответственно, то результирующий сигнал y (t) будет задерживаться на (t1 + t2). Математически это можно записать как —
Если x_ {1} (t) * x_ {2} (t) = y (t)
Тогда x_ {1} (t-t_ {1}) * x_ {2} (t-t_ {2}) = y [t- (t_ {1} + t_ {2})]
Решенные примеры
Пример 1 — Найти свертку сигналов u (t-1) и u (t-2).
Решение — Даны сигналы u (t-1) и u (t-2). Их свертка может быть сделана, как показано ниже —
y (t) = u (t-1) * u (t-2)
y (t) = \ int _ {- \ infty} ^ {+ \ infty} [u (t-1) .u (t-2)] dt
= r (t-1) + r (t-2)
= r (t-3)
Пример 2 — Найти свертку двух сигналов, заданных
x_ {1} (n) = \ lbrace 3, -2, 2 \ rbrace
x_ {2} (n) = \ begin {case} 2, & 0 \ leq n \ leq 4 \\ 0, & x> elsewhere \ end {case}
Решение —
x 2 (n) может быть декодирован как x_ {2} (n) = \ lbrace 2,2,2,2,2 \ rbrace Originalfirst
x 1 (n) предварительно задано = \ lbrace 3, -2,3 \ rbrace = 3-2Z ^ {- 1} + 2Z ^ {- 2}
Аналогично, x_ {2} (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4}
Результирующий сигнал,
X (Z) = X_ {1} (Z) X_ {2} (z)
= \ lbrace 3-2Z ^ {- 1} + 2Z ^ {- 2} \ rbrace \ times \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {-4} \ rbrace
= 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + 6Z ^ {- 4} + 6Z ^ {- 5}
Принимая обратное Z-преобразование, мы получим результирующий сигнал как
x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace Происхождение на первом
Пример 3 — Определить свертку следующих 2 сигналов —
x (n) = \ lbrace 2,1,0,1 \ rbrace
h (n) = \ lbrace 1,2,3,1 \ rbrace
Решение —
Взяв Z-преобразование сигналов, получим,
x (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 3}
И h (n) = 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3}
Теперь свертка двух сигналов означает умножение их Z-преобразований.
То есть Y (Z) = X (Z) \ times h (Z)
= \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 3} \ rbrace \ times \ lbrace 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} \ rbrace
= \ lbrace 2 + 5Z ^ {- 1} + 8Z ^ {- 2} + 6Z ^ {- 3} + 3Z ^ {- 4} + 3Z ^ {- 5} + Z ^ {- 6} \ rbrace
Принимая обратное Z-преобразование, результирующий сигнал может быть записан как;
y (n) = \ lbrace 2,5,8,6,6,1 \ rbrace Originalfirst
Цифровая обработка сигналов — статические системы
Некоторые системы имеют обратную связь, а некоторые нет. У тех, у кого нет систем обратной связи, их вывод зависит только от текущих значений ввода. Прошлая ценность данных не присутствует в то время. Эти типы систем известны как статические системы. Это также не зависит от будущих ценностей.
Поскольку эти системы не имеют прошлых записей, значит, они также не имеют никакой памяти. Поэтому мы говорим, что все статические системы являются системами без памяти. Давайте возьмем пример, чтобы понять эту концепцию намного лучше.
пример
Давайте проверим, являются ли следующие системы статическими или нет.
- y (t) = x (t) + x (t-1)
- y (t) = x (2t)
- y (t) = x = \ sin [x (t)]
а) y (t) = x (t) + x (t-1)
Здесь x (t) — текущая стоимость. Это не имеет никакого отношения к прошлым ценностям времени. Итак, это статическая система. Однако в случае x (t-1), если мы положим t = 0, он уменьшится до x (-1), который зависит от прошлого значения. Итак, это не статично. Поэтому здесь y (t) не является статической системой.
б) y (t) = x (2t)
Если подставить t = 2, результатом будет y (t) = x (4). Опять же, это зависит от будущей стоимости. Так что это тоже не статичная система.
в) y (t) = x = \ sin [x (t)]
В этом выражении мы имеем дело с синусоидальной функцией. Диапазон синусоидальной функции лежит в пределах от -1 до +1. Итак, какими бы значениями мы ни подставляли x (t), мы получим значение от -1 до +1. Поэтому мы можем сказать, что это не зависит от каких-либо прошлых или будущих ценностей. Следовательно, это статическая система.
Из приведенных выше примеров можно сделать следующие выводы —
- Любая система, имеющая сдвиг во времени, не является статичной.
- Любая система, имеющая сдвиг амплитуды, также не является статичной.
- Случаи интеграции и дифференциации также не являются статичными.
Цифровая обработка сигналов — динамические системы
Если система зависит от прошлого и будущего значения сигнала в любой момент времени, то она называется динамической системой. В отличие от статических систем, это не системы без памяти. Они хранят прошлые и будущие ценности. Поэтому им требуется память. Давайте лучше разберемся в этой теории на нескольких примерах.
Примеры
Узнайте, являются ли следующие системы динамическими.
а) y (t) = x (t + 1)
В этом случае, если мы положим t = 1 в уравнении, оно будет преобразовано в x (2), которое является будущим зависимым значением. Потому что здесь мы даем ввод как 1, но он показывает значение для х (2). Поскольку это сигнал, зависящий от будущего, очевидно, что это динамическая система.
б) y (t) = Real [x (t)]
= \ frac {[x (t) + x (t) ^ *]} {2}
В этом случае, какое бы значение мы ни установили, оно покажет сигнал реального времени. Он не зависит от будущих или прошлых ценностей. Следовательно, это не динамическая система, а статическая система.
в) y (t) = Четный [x (t)]
= \ frac {[x (t) + x (-t)]} {2}
Здесь, если мы подставим t = 1, один сигнал покажет x (1), а другой покажет x (-1), что является прошлым значением. Точно так же, если мы поставим t = -1, тогда один сигнал покажет x (-1), а другой покажет x (1), который является будущим значением. Поэтому ясно, что это случай динамической системы.
d) y (t) = \ cos [x (t)]
В этом случае, поскольку система является функцией косинуса, она имеет определенную область значений, которая лежит в диапазоне от -1 до +1. Поэтому, какие бы значения мы ни указали, мы получим результат в пределах указанного лимита. Следовательно, это статическая система
Из приведенных выше примеров можно сделать следующие выводы —
- Все случаи временного сдвига сигналов являются динамическими сигналами.
- В случае масштабирования времени все сигналы являются динамическими.
- Сигналы интеграции случаев являются динамическими сигналами.
Цифровая обработка сигналов — Причинно-следственные системы
Ранее мы видели, что система должна быть независимой от будущих и прошлых ценностей, чтобы стать статичной. В этом случае условие почти такое же с небольшой модификацией. Здесь, чтобы система была причинно-следственной, она должна быть независимой только от будущих значений. Это означает, что зависимость от прошлого не вызовет проблем для системы.
Причинные системы представляют собой практически или физически реализуемую систему. Давайте рассмотрим несколько примеров, чтобы понять это намного лучше.
Примеры
Рассмотрим следующие сигналы.
а) y (t) = x (t)
Здесь сигнал зависит только от текущих значений х. Например, если мы подставим t = 3, результат будет отображаться только в этот момент времени. Поэтому, поскольку она не зависит от будущей ценности, мы можем назвать ее Причинно-следственной системой.
б) y (t) = x (t-1)
Здесь система зависит от прошлых ценностей. Например, если мы подставим t = 3, выражение уменьшится до x (2), что является прошлым значением для нашего ввода. Ни в коем случае это не зависит от будущих ценностей. Следовательно, эта система также является причинно-следственной системой.
в) y (t) = x (t) + x (t + 1)
В этом случае система состоит из двух частей. Часть x (t), как мы обсуждали ранее, зависит только от текущих значений. Таким образом, нет проблем с этим. Однако, если мы возьмем случай x (t + 1), он явно зависит от будущих значений, потому что если мы положим t = 1, выражение уменьшится до x (2), который является будущим значением. Следовательно, это не причинно-следственная связь.
DSP — непричинные системы
Непричинная система прямо противоположна причинной системе. Если система зависит от будущих значений входных данных в любой момент времени, то система называется не причинной системой.
Примеры
Давайте возьмем несколько примеров и попытаемся понять это лучше.
а) y (t) = x (t + 1)
Мы уже обсуждали эту систему и в причинной системе. При любом вводе это приведет к уменьшению системы до ее будущего значения. Например, если мы положим t = 2, он уменьшится до x (3), что является будущим значением. Следовательно, система не является причинно-следственной.
б) y (t) = x (t) + x (t + 2)
В этом случае x (t) является чисто зависимой функцией текущей стоимости. Мы уже обсуждали, что функция x (t + 2) зависит от будущего, потому что для t = 3 она даст значения для x (5). Следовательно, это не причинно-следственная связь.
в) y (t) = x (t-1) + x (t)
В этой системе это зависит от настоящих и прошлых значений данного входа. Какие бы значения мы ни подставляли, это никогда не будет отражать будущую зависимость. Ясно, что это не не причинная система; скорее это причинно-следственная система.
DSP — Анти-Причинные Системы
Анти-причинная система — это лишь немного модифицированная версия не-причинной системы. Система зависит только от будущих значений входа. Он не зависит ни от настоящих, ни от прошлых ценностей.
Примеры
Узнайте, являются ли следующие системы анти-причинными.
а) y (t) = x (t) + x (t-1)
Система имеет две подфункции. Одна подфункция x (t + 1) зависит от будущего значения входа, а другая подфункция x (t) зависит только от настоящего. Поскольку система зависит от текущей стоимости, в дополнение к будущей стоимости, эта система не является анти-каузальной.
б) y (t) = x (t + 3)
Если мы проанализируем вышеупомянутую систему, мы увидим, что система зависит только от будущих значений системы, т.е. если мы положим t = 0, она уменьшится до x (3), который является будущим значением. Эта система является прекрасным примером противопричинной системы.
Цифровая обработка сигналов — линейные системы
Линейная система подчиняется законам суперпозиции. Этот закон является необходимым и достаточным условием для доказательства линейности системы. Помимо этого, система представляет собой комбинацию двух типов законов —
- Закон аддитивности
- Закон однородности
Как закон гомогенности, так и закон аддитивности показаны на рисунках выше. Однако существуют некоторые другие условия, чтобы проверить, является ли система линейной или нет.
Условия —
- Выход должен быть нулевым для нулевого ввода.
- В системе не должно быть нелинейных операторов.
Примеры нелинейных операторов —
(а) Тригонометрические операторы — Sin, Cos, Tan, Cot, Sec, Cosec и т. д.
(б) экспоненциальный, логарифмический, модуль, квадрат, куб и т. д.
(c) sa (i / p), Sinc (i / p), Sqn (i / p) и т. д.
Ни вход x, ни выход y не должны иметь этих нелинейных операторов.
Примеры
Выясним, являются ли следующие системы линейными.
а) y (t) = x (t) + 3
Эта система не является линейной системой, поскольку она нарушает первое условие. Если мы введем ввод как ноль, сделав x (t) = 0, то результат будет не нулевым.
б) y (t) = \ sin tx (t)
В этой системе, если мы дадим входное значение как ноль, выходное значение станет нулевым. Следовательно, первое условие явно выполнено. Опять же, нет нелинейного оператора, который был бы применен к x (t). Следовательно, второе условие также выполнено. Следовательно, система является линейной системой.
в) y (t) = \ sin (x (t))
В вышеприведенной системе первое условие выполняется, потому что если мы положим x (t) = 0, то на выходе также будет sin (0) = 0. Однако второе условие не выполняется, поскольку существует нелинейный оператор, который работает х (т). Следовательно, система не является линейной.
DSP — нелинейные системы
Если мы хотим определить эту систему, мы можем сказать, что системы, которые не являются линейными, являются нелинейными системами. Понятно, что в этом случае должны выполняться все условия, которые нарушаются в линейных системах.
условия
-
Выходной сигнал не должен быть нулевым, если входной сигнал равен нулю.
-
Любой нелинейный оператор может быть применен на входе или выходе, чтобы сделать систему нелинейной.
Выходной сигнал не должен быть нулевым, если входной сигнал равен нулю.
Любой нелинейный оператор может быть применен на входе или выходе, чтобы сделать систему нелинейной.
Примеры
Выяснить, являются ли данные системы линейными или нелинейными.
а) y (t) = e ^ {x (t)}
В вышеприведенной системе первое условие выполняется, потому что если мы введем ноль на входе, на выходе будет 1. Кроме того, экспоненциальный нелинейный оператор применяется к входу. Понятно, что это случай нелинейной системы.
б) y (t) = x (t + 1) + x (t-1)
Система вышеупомянутого типа имеет дело как с прошлыми, так и с будущими ценностями. Однако, если мы сделаем его входной ноль, то ни одно из его значений не существует. Следовательно, мы можем сказать, что если вход равен нулю, то масштабированная по времени и смещенная по времени версия ввода также будет равна нулю, что нарушает наше первое условие. Опять же, нет нелинейного оператора присутствует. Следовательно, второе условие также нарушается. Очевидно, что эта система не является нелинейной системой; скорее это линейная система.
DSP — Инвариантные по времени системы
Для системы, не зависящей от времени, вывод и ввод должны быть задержаны на некоторую единицу времени. Любая задержка, указанная на входе, должна быть отражена на выходе для системы, не зависящей от времени.
Примеры
а) y (T) = x (2T)
Если вышеприведенное выражение, оно сначала проходит через систему, а затем через задержку (как показано в верхней части рисунка); тогда результат станет x (2T-2t) . Теперь то же самое выражение сначала проходит через задержку, а затем через систему (как показано в нижней части рисунка). На выходе получится x (2T-t) .
Следовательно, система не является неизменной по времени системой.
б) y (T) = \ sin [x (T)]
Если сигнал сначала проходит через систему, а затем через процесс временной задержки, выходной сигнал будет \ sin x (Tt) . Точно так же, если система сначала проходит через задержку, а затем через систему, то результат будет равен \ sin x (Tt) . Мы можем ясно видеть, что оба выхода одинаковы. Следовательно, система не зависит от времени.
DSP — системы с переменным временем
Для системы с изменяющимся временем также выход и вход должны быть задержаны на некоторую постоянную времени, но задержка на входе не должна отражаться на выходе. Все случаи масштабирования времени являются примерами системы вариантов времени. Точно так же, когда коэффициент в системных отношениях является функцией времени, система также является вариантом времени.
Примеры
а) y (t) = x [\ cos T]
Если вышеупомянутый сигнал сначала проходит через систему, а затем через задержку, выходной сигнал будет x \ cos (Tt) . Если сначала пройти через задержку, а затем через систему, это будет x (\ cos Tt) . Поскольку выходы не совпадают, система является вариантом времени.
б) y (T) = \ cos Tx (T)
Если вышеприведенное выражение сначала проходит через систему, а затем через задержку, то на выходе будет \ cos (Tt) x (Tt) . Однако, если выражение пропускается сначала через задержку, а затем через систему, на выходе будет \ cos Tx (Tt) . Поскольку выходы не одинаковы, система явно зависит от времени.
Цифровая обработка сигналов — стабильные системы
Стабильная система удовлетворяет условию BIBO (ограниченный вход для ограниченного выхода). Здесь ограниченный означает конечный по амплитуде. Для стабильной системы вывод должен быть ограниченным или конечным, для конечного или ограниченного ввода в любой момент времени.
Некоторыми примерами ограниченных входных данных являются функции синуса, косинуса, постоянного тока, сигнум и единичного шага.
Примеры
а) y (t) = x (t) + 10
Здесь для определенного ограниченного входа мы можем получить определенный ограниченный выход, т. Е. Если положить x (t) = 2, y (t) = 12 , который ограничен по своей природе. Поэтому система стабильна.
б) y (t) = \ sin [x (t)]
В данном выражении мы знаем, что функции синуса имеют определенную границу значений, которая лежит между -1 и +1. Итак, какие бы значения мы ни подставляли в точке x (t), мы получим значения в пределах нашей границы. Поэтому система стабильна.
Цифровая обработка сигналов — нестабильные системы
Нестабильные системы не удовлетворяют условиям BIBO. Поэтому для ограниченного входа мы не можем ожидать ограниченного выхода в случае нестабильных систем.
Примеры
а) y (t) = tx (t)
Здесь для конечного ввода мы не можем ожидать конечного вывода. Например, если мы положим x (t) = 2 \ Rightarrow y (t) = 2t . Это не конечное значение, потому что мы не знаем значение t. Таким образом, он может быть ранжирован из любого места. Поэтому эта система не является стабильной. Это нестабильная система.
б) y (t) = \ frac {x (t)} {\ sin t}
Ранее мы обсуждали, что функция синуса имеет определенный диапазон от -1 до +1; но здесь он присутствует в знаменателе. Таким образом, в худшем случае, если мы положим t = 0 и функция синуса станет нулевой, тогда вся система будет стремиться к бесконечности. Следовательно, этот тип системы совсем не стабилен. Очевидно, что это нестабильная система.
DSP — Системные свойства решаемых примеров
Пример 1. Проверьте, является ли y (t) = x * (t) линейным или нелинейным.
Решение — функция представляет собой сопряжение ввода. Это можно проверить либо по первому закону однородности и закона аддитивности, либо по двум правилам. Тем не менее, проверка с помощью правил намного проще, поэтому мы пойдем по этому пути.
Если вход в систему равен нулю, выход также стремится к нулю. Поэтому наше первое условие выполнено. Нелинейный оператор не используется ни на входе, ни на выходе. Следовательно, система является линейной.
Пример 2. Проверьте, является ли y (t) = \ begin {case} x (t + 1), & t> 0 \\ x (t-1), & t \ leq 0 \ end {case} линейным или нелинейный
Решение — ясно, что мы можем видеть, что когда время становится меньше или равно нулю, вход становится нулевым. Таким образом, мы можем сказать, что при нулевом входе выход также равен нулю, и наше первое условие выполнено.
Опять же, нет ни нелинейного оператора, используемого на входе, ни на выходе. Следовательно, система является линейной.
Пример 3 — Проверьте, стабильно ли y (t) = \ sin tx (t) .
Решение — Предположим, что мы приняли значение x (t) равным 3. Здесь функция синуса умножена на нее, а максимальное и минимальное значение функции синуса изменяется от -1 до +1.
Следовательно, максимальное и минимальное значение всей функции также будет варьироваться от -3 до +3. Таким образом, система стабильна, потому что здесь мы получаем ограниченный вход для ограниченного выхода.
DSP — Z-Transform Введение
Дискретное временное преобразование Фурье (DTFT) существует для сигналов энергии и мощности. Z-преобразование также существует ни для сигнала типа энергии, ни для мощности (NENP), до определенной степени. Замена z = e ^ {jw} используется для преобразования Z-преобразования в DTFT только для абсолютно суммируемого сигнала.
Таким образом, Z-преобразование дискретного сигнала времени x (n) в степенном ряду можно записать как —
X (z) = \ sum_ {n- \ infty} ^ \ infty x (n) Z ^ {- n}
Вышеупомянутое уравнение представляет собой двустороннее уравнение Z-преобразования.
Как правило, когда сигнал Z-преобразован, он может быть представлен как —
X (Z) = Z [x (n)]
Или x (n) \ longleftrightarrow X (Z)
Если это непрерывный сигнал времени, то Z-преобразования не нужны, потому что используются преобразования Лапласа. Однако сигналы с дискретным временем можно анализировать только с помощью Z-преобразований.
Регион конвергенции
Область сходимости — это диапазон комплексной переменной Z в плоскости Z. Z-преобразование сигнала является конечным или сходящимся. Итак, ROC представляет собой тот набор значений Z, для которого X (Z) имеет конечное значение.
Свойства РПЦ
- РПЦ не включает в себя ни одного полюса.
- Для правостороннего сигнала ROC будет вне круга в Z-плоскости.
- Для левостороннего сигнала ROC будет внутри круга в Z-плоскости.
- Для устойчивости ROC включает единичный круг в Z-плоскости.
- Для двустороннего сигнала ROC является кольцом в Z-плоскости.
- Для сигнала конечной длительности ROC — это вся Z-плоскость.
Z-преобразование уникально характеризуется —
- Выражение X (Z)
- РПЦ X (Z)
Сигналы и их РПЦ
| х (п) | Х (Z) | РПЦ |
|---|---|---|
| \ Delta (п) | 1 | Вся плоскость Z |
| U (N) | 1 / (1-Z ^ {- 1}) | Mod (Z)> 1 |
| А ^ пи (п) | 1 / (1-Az ^ {- 1}) | Mod (Z)> Mod (а) |
| -A ^ ню (-п-1) | 1 / (1-Az ^ {- 1}) | Mod (Z) <Mod (а) |
| На ^ ню (п) | Az ^ {- 1} / (1-Az ^ {- 1}) ^ 2 | Mod (Z)> Mod (а) |
| -A ^ ню (-п-1) | Az ^ {- 1} / (1-Az ^ {- 1}) ^ 2 | Mod (Z) <Mod (а) |
| U (n) \ cos \ omega n | (Z ^ 2-Z \ cos \ omega) / (Z ^ 2-2Z \ cos \ omega +1) | Mod (Z)> 1 |
| U (n) \ sin \ omega n | (Z \ sin \ omega) / (Z ^ 2-2Z \ cos \ omega +1) | Mod (Z)> 1 |
пример
Найдем Z-преобразование и ROC сигнала, заданного как x (n) = \ lbrace 7,3,4,9,5 \ rbrace , где начало ряда равно 3.
Решение — Применяя формулу, которую мы имеем —
X (z) = \ sum_ {n = — \ infty} ^ \ infty x (n) Z ^ {- n}
= \ sum_ {n = -1} ^ 3 x (n) Z ^ {- n}
= x (-1) Z + x (0) + x (1) Z ^ {- 1} + x (2) Z ^ {- 2} + x (3) Z ^ {- 3}
= 7Z + 3 + 4Z ^ {- 1} + 9Z ^ {- 2} + 5Z ^ {- 3}
ROC — вся Z-плоскость, исключая Z = 0, ∞, -∞
DSP — Z-Transform Свойства
В этой главе мы поймем основные свойства Z-преобразований.
линейность
В нем говорится, что когда два или более отдельных дискретных сигнала умножаются на константы, их соответствующие Z-преобразования также будут умножаться на одни и те же константы.
Математически,
a_1x_1 (n) + a_2x_2 (n) = a_1X_1 (z) + a_2X_2 (z)
Доказательство — Мы знаем это,
X (Z) = \ sum_ {n = — \ infty} ^ \ infty x (n) Z ^ {- n}
= \ sum_ {n = — \ infty} ^ \ infty (a_1x_1 (n) + a_2x_2 (n)) Z ^ {- n}
= a_1 \ sum_ {n = — \ infty} ^ \ infty x_1 (n) Z ^ {- n} + a_2 \ sum_ {n = — \ infty} ^ \ infty x_2 (n) Z ^ {- n}
= a_1X_1 (z) + a_2X_2 (z) (доказано)
Здесь ROC — это ROC_1 \ bigcap ROC_2 .
Временной сдвиг
Свойство сдвига во времени показывает, как изменение во временной области в дискретном сигнале повлияет на Z-область, которая может быть записана как;
x (n-n_0) \ longleftrightarrow X (Z) Z ^ {- n}
Или x (n-1) \ longleftrightarrow Z ^ {- 1} X (Z)
Доказательство —
Пусть y (P) = X (PK)
Y (z) = \ sum_ {p = — \ infty} ^ \ infty y (p) Z ^ {- p}
= \ sum_ {p = — \ infty} ^ \ infty (x (pk)) Z ^ {- p}
Пусть s = pk
= \ sum_ {s = — \ infty} ^ \ infty x (s) Z ^ {- (s + k)}
= \ sum_ {s = — \ infty} ^ \ infty x (s) Z ^ {- s} Z ^ {- k}
= Z ^ {- k} [\ sum_ {s = — \ infty} ^ \ infty x (m) Z ^ {- s}]
= Z ^ {- k} X (Z) (доказано)
Здесь ROC может быть записано как Z = 0 (p> 0) или Z = ∞ (p <0)
пример
U (n) и U (n-1) могут быть построены следующим образом
Z-преобразование U (n) может быть записано как;
\ sum_ {n = — \ infty} ^ \ infty [U (n)] Z ^ {- n} = 1
Z-преобразование U (n-1) может быть записано как;
\ sum_ {n = — \ infty} ^ \ infty [U (n-1)] Z ^ {- n} = Z ^ {- 1}
Так что здесь x (n-n_0) = Z ^ {- n_0} X (Z) (доказано)
Масштабирование времени
Свойство Time Scaling сообщает нам, какой будет Z-область сигнала, когда время масштабируется в его дискретной форме, которую можно записать как;
a ^ nx (n) \ longleftrightarrow X (a ^ {- 1} Z)
Доказательство —
Пусть y (p) = a ^ {p} x (p)
Y (P) = \ sum_ {p = — \ infty} ^ \ infty y (p) Z ^ {- p}
= \ sum_ {p = — \ infty} ^ \ infty a ^ px (p) Z ^ {- p}
= \ sum_ {p = — \ infty} ^ \ infty x (p) [a ^ {- 1} Z] ^ {- p}
= X (a ^ {- 1} Z) (следовательно, доказано)
ROC: = Mod (ar1) <Mod (Z) <Mod (ar2), где Mod = Модуль
пример
Определим Z-преобразование x (n) = a ^ n \ cos \ omega n , используя свойство масштабирования по времени.
Решение —
Мы уже знаем, что Z-преобразование сигнала \ cos (\ omega n) определяется выражением —
\ sum_ {n = — \ infty} ^ \ infty (\ cos \ omega n) Z ^ {- n} = (Z ^ 2-Z \ cos \ omega) / (Z ^ 2-2Z \ cos \ omega +1)
Теперь, применяя свойство масштабирования по времени, Z-преобразование a ^ n \ cos \ omega n можно записать в виде;
\ sum_ {n = — \ infty} ^ \ infty (a ^ n \ cos \ omega n) Z ^ {- n} = X (a ^ {- 1} Z)
= [(a ^ {- 1} Z) ^ 2- (a ^ {- 1} Z \ cos \ omega n)] / ((a ^ {- 1} Z) ^ 2-2 (a ^ {- 1} Z \ cos \ omega n) +1)
= Z (Za \ cos \ omega) / (Z ^ 2-2az \ cos \ omega + a ^ 2)
Последовательная дифференциация
Свойство последовательного дифференцирования показывает, что Z-преобразование будет иметь место, когда мы дифференцируем дискретный сигнал во временной области по времени. Это показано ниже.
\ frac {dx (n)} {dn} = (1-Z ^ {- 1}) X (Z)
Доказательство —
Рассмотрим LHS уравнения — \ frac {dx (n)} {dn}
= \ frac {[x (n) -x (n-1)]} {[n- (n-1)]}
= x (n) -X (n-1)
= x (Z) -Z ^ {- 1} x (Z)
= (1-Z ^ {- 1}) x (Z) (доказано)
ROC: R1 <Mod (Z) <R2
пример
Найдем Z-преобразование сигнала, заданного как x (n) = n ^ 2u (n)
По свойству мы можем написать
Zz [nU (n)] = -Z \ frac {dZ [U (n)]} {dz}
= -Z \ frac {d [\ frac {Z} {Z-1}]} {dZ}
= Z / ((Z-1) ^ 2
= y (let)
Теперь Z [ny] можно узнать, снова применив свойство,
Z (n, y) = -Z \ frac {dy} {dz}
= -Z \ frac {d [Z / (Z-1) ^ 3]} {dz}
= Z (Z + 1) / (Z-1) ^ 2
свертка
Это показывает изменение в Z-области системы, когда происходит свертка в форме дискретного сигнала, которая может быть записана как —
x_1 (n) * x_2 (n) \ longleftrightarrow X_1 (Z) .X_2 (Z)
Доказательство —
X (Z) = \ sum_ {n = — \ infty} ^ \ infty x (n) Z ^ {- n}
= \ sum_ {n = — \ infty} ^ \ infty [\ sum_ {k = — \ infty} ^ \ infty x_1 (k) x_2 (nk)] Z ^ {- n}
= \ sum_ {k = — \ infty} ^ \ infty x_1 (k) [\ sum_n ^ \ infty x_2 (nk) Z ^ {- n}]
= \ sum_ {k = — \ infty} ^ \ infty x_1 (k) [\ sum_ {n = — \ infty} ^ \ infty x_2 (nk) Z ^ {- (nk)} Z ^ {- k}]
Пусть nk = l, тогда приведенное выше уравнение можно записать в виде —
X (Z) = \ sum_ {k = — \ infty} ^ \ infty x_1 (k) [Z ^ {- k} \ sum_ {l = — \ infty} ^ \ infty x_2 (l) Z ^ {- l }]
= \ sum_ {k = — \ infty} ^ \ infty x_1 (k) X_2 (Z) Z ^ {- k}
= X_2 (Z) \ sum_ {k = — \ infty} ^ \ infty x_1 (Z) Z ^ {- k}
= X_1 (Z) .X_2 (Z) (доказано)
ROC: ROC \ bigcap ROC2
пример
Давайте найдем свертку, заданную двумя сигналами
x_1 (n) = \ lbrace 3, -2,2 \ rbrace … (уравнение 1)
x_2 (n) = \ lbrace 2,0 \ leq 4 \ quad и \ quad 0 \ quad elsewhere \ rbrace … (уравнение 2)
Z-преобразование первого уравнения можно записать в виде;
\ sum_ {n = — \ infty} ^ \ infty x_1 (n) Z ^ {- n}
= 3-2Z ^ {- 1} + 2Z ^ {- 2}
Z-преобразование второго сигнала можно записать в виде;
\ sum_ {n = — \ infty} ^ \ infty x_2 (n) Z ^ {- n}
= 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4}
Итак, свертка двух вышеупомянутых сигналов определяется как —
X (Z) = [x_1 (Z) ^ * x_2 (Z)]
= [3-2Z ^ {- 1} + 2Z ^ {- 2}] \ times [2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4 }]
= 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + … \ quad … \ quad …
Взяв обратное Z-преобразование, мы получим,
x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace
Теорема начального значения
Если x (n) является причинной последовательностью, которая имеет свое Z-преобразование как X (z), то теорема о начальном значении может быть записана как;
X (n) (at \ quad n = 0) = \ lim_ {z \ to \ infty} X (z)
Доказательство — Мы знаем это,
X (Z) = \ sum_ {n = 0} ^ \ infty x (n) Z ^ {- n}
Расширяя вышеприведенные серии, получаем;
= X (0) Z ^ 0 + X (1) Z ^ {- 1} + X (2) Z ^ {- 2} + … \ quad …
= X (0) \ times 1 + X (1) Z ^ {- 1} + X (2) Z ^ {- 2} + … \ quad …
В приведенном выше случае, если Z → ∞, то Z ^ {- n} \ rightarrow 0 (потому что n> 0)
Поэтому мы можем сказать;
\ lim_ {z \ to \ infty} X (z) = X (0) (доказано)
Окончательная Теорема Значения
Теорема об окончательном значении утверждает, что если Z-преобразование сигнала представлено в виде X (Z) и все полюсы находятся внутри круга, то его окончательное значение обозначается как x (n) или X (∞) и может быть записано как —
X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {- 1})]]
Условия —
- Это применимо только для причинных систем.
- В X (Z) (1-Z ^ {- 1}) должны быть полюсы внутри единичного круга в Z-плоскости.
Доказательство — мы знаем, что
Z ^ + [x (n + 1) -x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (n + 1) -x (п)]
\ Rightarrow Z ^ + [x (n + 1)] — Z ^ + [x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (п + 1) -x (п)]
\ Rightarrow Z [X (Z) ^ + — x (0)] — X (Z) ^ + = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {- n} [x (п + 1) -x (п)]
Здесь мы можем применить расширенное свойство одностороннего Z-преобразования. Таким образом, вышеприведенное уравнение может быть переписано как;
Z ^ + [x (n + 1)] = Z [X (2) ^ + — x (0) Z ^ 0] = Z [X (Z) ^ + — x (0)]
Теперь, положив z = 1 в приведенном выше уравнении, мы можем расширить приведенное выше уравнение —
\ lim_ {k \ to \ infty} {[x (1) -x (0) + x (6) -x (1) + x (3) -x (2) + … \ quad … \ четырехъядерных … + х (х + 1) -x (к)]}
Это может быть сформулировано как;
X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {- 1})]] (доказано)
пример
Найдем начальное и конечное значение x (n), сигнал которого определяется
X (Z) = 2 + 3Z ^ {- 1} + 4Z ^ {- 2}
Решение — Давайте сначала найдем начальное значение сигнала, применив теорему
x (0) = \ lim_ {z \ to \ infty} X (Z)
= \ lim_ {z \ to \ infty} [2 + 3Z ^ {- 1} + 4Z ^ {- 2}]
= 2 + (\ frac {3} {\ infty}) + (\ frac {4} {\ infty}) = 2
Теперь давайте найдем окончательное значение сигнала, применяя теорему
x (\ infty) = \ lim_ {z \ to \ infty} [(1-Z ^ {- 1}) X (Z)]
= \ lim_ {z \ to \ infty} [(1-Z ^ {- 1}) (2 + 3Z ^ {- 1} + 4Z ^ {- 2})]
= \ lim_ {z \ to \ infty} [2 + Z ^ {- 1} + Z ^ {- 2} -4Z ^ {- 3}]
= 2 + 1 + 1-4 = 0
Некоторые другие свойства Z-преобразования перечислены ниже —
Дифференциация по частоте
Это дает изменение в Z-области сигнала, когда его дискретный сигнал дифференцируется по времени.
nx (n) \ longleftrightarrow -Z \ frac {dX (z)} {dz}
Его РПЦ можно записать как;
r_2 <Mod (Z) <r_1
пример
Найдем значение x (n) через дифференцирование по частоте, дискретный сигнал которого в Z-области задается как x (n) \ longleftrightarrow X (Z) = log (1 + aZ ^ {- 1})
По свойству мы можем написать, что
nx (n) \ longleftrightarrow -Z \ frac {dx (Z)} {dz}
= -Z [\ frac {-aZ ^ {- 2}} {1 + aZ ^ {- 1}}]
= (aZ ^ {- 1}) / (1 + aZ ^ {- 1})
= 1-1 / (1 + aZ ^ {- 1})
nx (n) = \ delta (n) — (- a) ^ nu (n)
\ Rightarrow x (n) = 1 / n [\ delta (n) — (- a) ^ nu (n)]
Умножение во времени
Это дает изменение в Z-области сигнала, когда умножение происходит на уровне дискретного сигнала.
x_1 (n) .x_2 (n) \ longleftrightarrow (\ frac {1} {2 \ Pi j}) [X1 (Z) * X2 (Z)]
Спряжение во времени
Это изображает представление сопряженного дискретного сигнала в Z-области.
X ^ * (n) \ longleftrightarrow X ^ * (Z ^ *)
DSP — Z-Transform Существование
Система, которая имеет системную функцию, может быть стабильной, только если все полюса лежат внутри единичного круга. Сначала мы проверяем, является ли система причинной или нет. Если система является причинно-следственной, то мы идем для определения ее стабильности BIBO; где стабильность BIBO относится к ограниченному входу для ограниченного выходного условия.
Это можно записать как;
Mod (X (Z)) <\ infty
= Mod (\ sum x (n) Z ^ {- n}) <\ infty
= \ sum Mod (x (n) Z ^ {- n}) <\ infty
= \ sum Mod [x (n) (re ^ {jw}) ^ {- n}] <0
= \ sum Mod [x (n) r ^ {- n}] Mod [e ^ {- jwn}] <\ infty
= \ sum_ {n = — \ infty} ^ \ infty Mod [x (n) r ^ {- n}] <\ infty
Вышеупомянутое уравнение показывает условие существования Z-преобразования.
Однако условием существования сигнала DTFT является
\ sum_ {n = — \ infty} ^ \ infty Mod (x (n) <\ infty
Пример 1
Попробуем выяснить Z-преобразование сигнала, которое задается как
x (n) = — (- 0.5) ^ {- n} u (-n) + 3 ^ nu (n)
= — (- 2) ^ nu (n) + 3 ^ nu (n)
Решение — Здесь для — (- 2) ^ nu (n) РПЦ является левой стороной и Z <2
Для 3 ^ nu (n) ROC является правосторонним и Z> 3
Следовательно, здесь Z-преобразование сигнала не будет существовать, потому что нет общей области.
Пример 2
Попробуем выяснить Z-преобразование сигнала, заданного
x (n) = -2 ^ nu (-n-1) + (0,5) ^ nu (n)
Решение — Здесь для -2 ^ nu (-n-1) ROC сигнала левосторонний и Z <2
Для сигнала (0.5) ^ nu (n) ROC является правосторонним и Z> 0.5
Таким образом, общая РПЦ формируется как 0,5 <Z <2
Следовательно, Z-преобразование можно записать как;
X (Z) = \ lbrace \ frac {1} {1-2Z ^ {- 1}} \ rbrace + \ lbrace \ frac {1} {(1-0.5Z) ^ {- 1}} \ rbrace
Пример 3
Попробуем выяснить Z-преобразование сигнала, которое задается как x (n) = 2 ^ {r (n)}
Решение — r (n) — сигнал линейного изменения. Таким образом, сигнал может быть записан как;
x (n) = 2 ^ {nu (n)} \ lbrace 1, n <0 (u (n) = 0) \ quad и \ quad2 ^ n, n \ geq 0 (u (n) = 1) \ rbrace
= u (-n-1) + 2 ^ nu (n)
Здесь для сигнала u (-n-1) и ROC Z <1 и для 2 ^ nu (n) с ROC Z = 2.
Таким образом, Z-преобразование сигнала не будет существовать.
Z-преобразование для каузальной системы
Причинная система может быть определена как h (n) = 0, n <0 . Для причинной системы ROC будет вне круга в Z-плоскости.
H (Z) = \ displaystyle \ sum \ limit_ {n = 0} ^ {\ infty} h (n) Z ^ {- n}
Расширяя вышеприведенное уравнение,
H (Z) = h (0) + h (1) Z ^ {- 1} + h (2) Z ^ {- 2} + … \ quad … \ quad …
= N (Z) / D (Z)
Для причинных систем расширение Передаточной функции не включает положительные степени Z. Для причинной системы порядок числителя не может превышать порядок знаменателя. Это можно записать как
\ lim_ {z \ rightarrow \ infty} H (Z) = h (0) = 0 \ quad или \ quad Finite
Для устойчивости причинной системы полюсы Передаточной функции должны быть внутри единичного круга в Z-плоскости.
Z-преобразование для анти-причинной системы
Анти-причинная система может быть определена как h (n) = 0, n \ geq 0 . Для анти-причинной системы полюсы передаточной функции должны лежать вне единичного круга в Z-плоскости. Для анти-каузальной системы ROC будет внутри круга в Z-плоскости.
DSP — Z-Transform Inverse
Если мы хотим проанализировать систему, которая уже представлена в частотной области, как дискретный сигнал времени, то мы переходим к обратному Z-преобразованию.
Математически это можно представить как;
x (n) = Z ^ {- 1} X (Z)
где x (n) — сигнал во временной области, а X (Z) — сигнал в частотной области.
Если мы хотим представить вышеприведенное уравнение в интегральном формате, мы можем записать его в виде
x (n) = (\ frac {1} {2 \ Pi j}) \ oint X (Z) Z ^ {- 1} dz
Здесь интеграл по замкнутому пути C. Этот путь находится внутри ROC x (z) и содержит начало координат.
Методы поиска обратного Z-преобразования
Когда анализ необходим в дискретном формате, мы преобразуем сигнал частотной области обратно в дискретный формат посредством обратного Z-преобразования. Мы следуем следующим четырем способам определения обратного Z-преобразования.
- Длинный метод деления
- Метод расширения частичной дроби
- Остаточный или контурный интегральный метод
Длинный метод деления
В этом методе Z-преобразование сигнала x (z) может быть представлено как отношение многочлена, как показано ниже;
х (г) = Н (Z) / D (Z),
Теперь, если мы продолжим делить числитель на знаменатель, то получим ряд, как показано ниже
X (z) = x (0) + x (1) Z ^ {- 1} + x (2) Z ^ {- 2} + … \ quad … \ quad …
Вышеприведенная последовательность представляет серию обратных Z-преобразований данного сигнала (для n≥0), и вышеуказанная система является причинно-следственной.
Однако при n <0 ряд можно записать в виде;
x (z) = x (-1) Z ^ 1 + x (-2) Z ^ 2 + x (-3) Z ^ 3 + … \ quad … \ quad …
Метод частичного расширения фракции
Здесь также сигнал выражается первым в форме N (z) / D (z).
Если это рациональная дробь, она будет представлена следующим образом;
x (z) = b_0 + b_1Z ^ {- 1} + b_2Z ^ {- 2} + … \ quad … \ quad … + b_mZ ^ {- m}) / (a_0 + a_1Z ^ { -1} + a_2Z ^ {- 2} + … \ четырехъядерных … \ четырехъядерных … + a_nZ ^ {- N})
Вышеупомянутое неуместно, когда m <n и ≠ 0
Если соотношение не является правильным (то есть, неправильным), тогда мы должны преобразовать его в правильную форму, чтобы решить.
Остаточный или контурный интегральный метод
В этом методе мы получаем обратное Z-преобразование x (n) суммированием вычетов [x (z) Z ^ {n-1}] на всех полюсах. Математически это может быть выражено как
x (n) = \ displaystyle \ sum \ limit_ {все \ четырехугольные полюса \ quad X (z)} вычеты \ quad of [x (z) Z ^ {n-1}]]
Здесь вычет для любого полюса порядка m при z = \ beta равен
Остатки = \ frac {1} {(m-1)!} \ Lim_ {Z \ rightarrow \ beta} \ lbrace \ frac {d ^ {m-1}} {dZ ^ {m-1}} \ lbrace (Z- \ бета) ^ тХ (г) Z ^ {N-1} \ rbrace
DSP — Z-Transform Решенные Примеры
Пример 1
Найти ответ системы s (n + 2) -3s (n + 1) + 2s (n) = \ delta (n) , когда все начальные условия равны нулю.
Решение — Взяв Z-преобразование с обеих сторон вышеприведенного уравнения, получим
S (z) Z ^ 2-3S (z) Z ^ 1 + 2S (z) = 1
\ Rightarrow S (z) \ lbrace Z ^ 2-3Z + 2 \ rbrace = 1
\ Rightarrow S (z) = \ frac {1} {\ lbrace z ^ 2-3z + 2 \ rbrace} = \ frac {1} {(z-2) (z-1)} = \ frac {\ alpha _1} {z-2} + \ frac {\ alpha _2} {z-1}
\ Rightarrow S (z) = \ frac {1} {z-2} — \ frac {1} {z-1}
Взяв обратное Z-преобразование приведенного выше уравнения, получим
S (n) = Z ^ {- 1} [\ frac {1} {Z-2}] — Z ^ {- 1} [\ frac {1} {Z-1}]
= 2 ^ {n-1} -1 ^ {n-1} = -1 + 2 ^ {n-1}
Пример 2
Найдите системную функцию H (z) и отклик единичной выборки h (n) системы, разностное уравнение которой описано как
y (n) = \ frac {1} {2} y (n-1) + 2x (n)
где y (n) и x (n) — выход и вход системы соответственно.
Решение — Взяв Z-преобразование приведенного выше разностного уравнения, получим
y (z) = \ frac {1} {2} Z ^ {- 1} Y (Z) + 2X (z)
= Y (Z) [1- \ frac {1} {2} Z ^ {- 1}] = 2X (Z)
= H (Z) = \ frac {Y (Z)} {X (Z)} = \ frac {2} {[1- \ frac {1} {2} Z ^ {- 1}]}
Эта система имеет полюс в Z = \ frac {1} {2} и Z = 0 и H (Z) = \ frac {2} {[1- \ frac {1} {2} Z ^ {-1}]}
Следовательно, принимая обратное Z-преобразование вышеупомянутого, мы получаем
h (n) = 2 (\ frac {1} {2}) ^ nU (n)
Пример 3
Определить Y (z), n≥0 в следующем случае —
y (n) + \ frac {1} {2} y (n-1) — \ frac {1} {4} y (n-2) = 0 \ quad данным \ quad y (-1) = y ( -2) = 1
Решение — Применяя Z-преобразование к вышеприведенному уравнению, получаем
Y (Z) + \ гидроразрыва {1} {2} [Z ^ {- 1} Y (Z) + Y (-1)] — \ гидроразрыва {1} {4} [Z ^ {- 2} У ( Z) + Z ^ {- 1} Y (-1) +4 (-2)] = 0
\ Rightarrow Y (Z) + \ frac {1} {2Z} Y (Z) + \ frac {1} {2} — \ frac {1} {4Z ^ 2} Y (Z) — \ frac {1} {4Z} — \ frac {1} {4} = 0
\ Rightarrow Y (Z) [1+ \ frac {1} {2Z} — \ frac {1} {4Z ^ 2}] = \ frac {1} {4Z} — \ frac {1} {2}
\ Rightarrow Y (Z) [\ frac {4Z ^ 2 + 2Z-1} {4Z ^ 2}] = \ frac {1-2Z} {4Z}
\ Rightarrow Y (Z) = \ frac {Z (1-2Z)} {4Z ^ 2 + 2Z-1}
Цифровая обработка сигналов — DFT Введение
Как и преобразование Фурье с непрерывным сигналом времени, преобразование Фурье с дискретным временем может использоваться для представления дискретной последовательности в ее эквивалентном представлении в частотной области и системе дискретного времени LTI и для разработки различных вычислительных алгоритмов.
X (jω) в непрерывном FT является непрерывной функцией от x (n). Однако DFT имеет дело с представлением x (n) с выборками его спектра X (ω). Следовательно, этот математический инструмент имеет большое значение в вычислительном отношении в удобном представлении. Как периодические, так и непериодические последовательности могут быть обработаны с помощью этого инструмента. Периодические последовательности должны быть выбраны путем расширения периода до бесконечности.
Выборка частотной области
Из введения ясно, что нам нужно знать, как пройти выборку в частотной области, то есть выборку X (ω). Следовательно, связь между дискретизированным преобразованием Фурье и DFT устанавливается следующим образом.
Точно так же периодические последовательности могут соответствовать этому инструменту, расширяя период N до бесконечности.
Пусть непериодическая последовательность: X (n) = \ lim_ {N \ to \ infty} x_N (n)
Определяя его преобразование Фурье,
X (\ omega) = \ sum_ {n = — \ infty} ^ \ infty x (n) e ^ {- jwn} X (K \ delta \ omega)
Здесь X (ω) дискретизируется периодически, на каждом интервале радиан δω.
Поскольку X (ω) является периодическим в 2π радианах, нам требуются выборки только в фундаментальном диапазоне. Образцы отбираются через равноотстоящие интервалы в диапазоне частот 0≤ω≤2π. Интервал между эквивалентными интервалами составляет \ delta \ omega = \ frac {2 \ pi} {N} k радиан.
Теперь оцениваем, \ omega = \ frac {2 \ pi} {N} k
X (\ frac {2 \ pi} {N} k) = \ sum_ {n = — \ infty} ^ \ infty x (n) e ^ {- j2 \ pi nk / N}, … eq ( 2)
где k = 0,1, …… N-1
Подразделив вышеперечисленное и поменяв порядок суммирования
X (\ frac {2 \ pi} {N} k) = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} [\ displaystyle \ sum \ limit_ {l = — \ infty} ^ \ infty x (n-Nl)] e ^ {- j2 \ pi nk / N} … eq (3)
\ sum_ {l = — \ infty} ^ \ infty x (n-Nl) = x_p (n) = \ quad периодическая \ quad-функция \ quad \ quad period \ quad N \ quad и \ quad его \ quad Фурье \ quad series \ quad = \ sum_ {k = 0} ^ {N-1} C_ke ^ {j2 \ pi nk / N}
где n = 0,1,… .., N-1; ‘p’ — периодическая сущность или функция
Коэффициенты Фурье:
C_k = \ frac {1} {N} \ sum_ {n = 0} ^ {N-1} x_p (n) e ^ {- j2 \ pi nk / N} k = 0,1,…, N- 1 … экв (4)
Сравнивая уравнения 3 и 4, получим;
NC_k = X (\ frac {2 \ pi} {N} k) k = 0,1,…, N-1 … eq (5)
NC_k = X (\ frac {2 \ pi} {N} k) = X (e ^ {jw}) = \ displaystyle \ sum \ limit_ {n = — \ infty} ^ \ infty x_p (n) e ^ { -j2 \ pi nk / N} … eq (6)
Из разложения в ряд Фурье
x_p (n) = \ frac {1} {N} \ displaystyle \ sum \ limit_ {k = 0} ^ {N-1} NC_ke ^ {j2 \ pi nk / N} = \ frac {1} {N} \ sum_ {k = 0} ^ {N-1} X (\ frac {2 \ pi} {N} k) e ^ {j2 \ pi nk / N} … eq (7)
Где n = 0,1,…, N-1
Здесь мы получили периодический сигнал от X (ω). x (n) можно извлечь только из x_p (n) , если во временной области нет псевдонимов. N \ geq L
N = период x_p (n) L = период x (n)
x (n) = \ begin {case} x_p (n), & 0 \ leq n \ leq N-1 \\ 0, & Иначе \ end {case}
Отображение достигается таким образом.
Свойства ДПФ
линейность
В нем говорится, что ДПФ комбинации сигналов равен сумме ДПФ отдельных сигналов. Возьмем два сигнала x 1 (n) и x 2 (n), чьи ДПФ s равны X 1 (ω) и X 2 (ω) соответственно. Так что если
x_1 (n) \ rightarrow X_1 (\ omega) и x_2 (n) \ rightarrow X_2 (\ omega)
Тогда ax_1 (n) + bx_2 (n) \ rightarrow aX_1 (\ omega) + bX_2 (\ omega)
где а и б постоянные.
симметричность
Свойства симметрии DFT могут быть получены аналогично тому, как мы получили свойства симметрии DTFT. Мы знаем, что ДПФ последовательности x (n) обозначается через X (K). Теперь, если x (n) и X (K) являются комплексными последовательностями, то это можно представить как
x (n) = x_R (n) + jx_1 (n), 0 \ leq n \ leq N-1
И X (K) = X_R (K) + jX_1 (K), 0 \ leq K \ leq N-1
Свойство двойственности
Рассмотрим сигнал x (n), ДПФ которого определяется как X (K). Пусть последовательность с конечной продолжительностью будет X (N). Тогда согласно теореме двойственности
Если x (n) \ longleftrightarrow X (K)
Тогда X (N) \ longleftrightarrow Nx [((- k)) _ N]
Таким образом, используя эту теорему, если мы знаем DFT, мы можем легко найти последовательность с конечной продолжительностью.
Комплекс сопряженных свойств
Предположим, существует сигнал x (n), ДПФ которого также известен нам как X (K). Теперь, если комплексное сопряжение сигнала задано как x * (n), то мы можем легко найти ДПФ без особых вычислений, используя теорему, показанную ниже.
Если x (n) \ longleftrightarrow X (K)
Тогда x * (n) \ longleftrightarrow X * ((K)) _ N = X * (NK)
Круговой сдвиг частоты
Умножение последовательности x (n) на комплексную экспоненциальную последовательность e ^ {j2 \ Pi kn / N} эквивалентно круговому сдвигу ДПФ на L единиц частоты. Это двойственное свойство кругового сдвига во времени.
Если x (n) \ longleftrightarrow X (K)
Тогда x (n) e ^ {j2 \ Pi Kn / N} \ longleftrightarrow X ((KL)) _ N
Умножение двух последовательностей
Если имеется два сигнала x 1 (n) и x 2 (n), и их соответствующие ДПФ представляют собой Х 1 (k) и Х 2 (К), то умножение сигналов во временной последовательности соответствует циклической свертке их ДПФ.
Если, x_1 (n) \ longleftrightarrow X_1 (K) \ quad \ & \ quad x_2 (n) \ longleftrightarrow X_2 (K)
Тогда x_1 (n) \ times x_2 (n) \ longleftrightarrow X_1 (K) © X_2 (K)
Теорема Парсеваля
Для комплексных последовательностей x (n) и y (n) в целом
Если x (n) \ longleftrightarrow X (K) \ quad \ & \ quad y (n) \ longleftrightarrow Y (K)
Тогда \ sum_ {n = 0} ^ {N-1} x (n) y ^ * (n) = \ frac {1} {N} \ sum_ {k = 0} ^ {N-1} X ( K) Y ^ * (K)
DSP — преобразование частоты времени DFT
Мы знаем, что когда \ omega = 2 \ pi K / N и N \ rightarrow \ infty, \ omega становится непрерывной переменной и ограничивает суммирование, равное — \ infty , до + \ infty .
Следовательно,
NC_k = X (\ frac {2 \ pi} {N} k) = X (e ^ {j \ omega}) = \ displaystyle \ sum \ limit_ {n = — \ infty} ^ \ infty x (n) e ^ {\ frac {-j2 \ pi nk} {N}} = \ displaystyle \ sum \ limit_ {n = — \ infty} ^ \ infty x (n) e ^ {- j \ omega n}
Дискретное временное преобразование Фурье (DTFT)
Мы знаем, что X (e ^ {j \ omega}) = \ sum_ {n = — \ infty} ^ \ infty x (n) e ^ {- j \ omega n}
Где X (e ^ {j \ omega}) непрерывен и периодичен по ω и имеет период 2π. … эк (1)
Сейчас,
x_p (n) = \ sum_ {k = 0} ^ {N-1} NC_ke ^ {j2 \ pi nk / N} … из ряда Фурье
x_p (n) = \ frac {1} {2 \ pi} \ sum_ {k = 0} ^ {N-1} NC_ke ^ {j2 \ pi nk / N} \ times \ frac {2 \ pi} {N }
ω становится непрерывным и \ frac {2 \ pi} {N} \ rightarrow d \ omega по причинам, указанным выше.
x (n) = \ frac {1} {2 \ pi} \ int_ {n = 0} ^ {2 \ pi} X (e ^ {j \ omega}) e ^ {j \ omega n} d \ omega … Eq (2)
Обратное преобразование Фурье с дискретным временем
Символично,
x (n) \ Longleftrightarrow x (e ^ {j \ omega}) (пара преобразований Фурье)
Необходимое и достаточное условие существования дискретного временного преобразования Фурье для непериодической последовательности x (n) является абсолютным суммируемым.
то есть \ sum_ {n = — \ infty} ^ \ infty | x (n) | <\ infty
Свойства DTFT
-
Линейность : a_1x_1 (n) + a_2x_2 (n) \ Leftrightarrow a_1X_1 (e ^ {j \ omega}) + a_2X_2 (e ^ {j \ omega})
-
Сдвиг времени — x (nk) \ Leftrightarrow e ^ {- j \ omega k} .X (e ^ {j \ omega})
-
Обращение времени — x (-n) \ Leftrightarrow X (e ^ {- j \ omega})
-
Сдвиг частоты — e ^ {j \ omega _0n} x (n) \ Leftrightarrow X (e ^ {j (\ omega — \ omega _0)})
-
Область частот дифференцирования — nx (n) = j \ frac {d} {d \ omega} X (e ^ {j \ omega})
-
Свертка — x_1 (n) * x_2 (n) \ Leftrightarrow X_1 (e ^ {j \ omega}) \ times X_2 (e ^ {j \ omega})
-
Умножение — x_1 (n) \ times x_2 (n) \ Leftrightarrow X_1 (e ^ {j \ omega}) * X_2 (e ^ {j \ omega})
-
Соотношение — y_ {x_1 \ times x_2} (l) \ Leftrightarrow X_1 (e ^ {j \ omega}) \ times X_2 (e ^ {j \ omega})
-
Теорема модуляции — x (n) \ cos \ omega _0n = \ frac {1} {2} [X_1 (e ^ {j (\ omega + \ omega _0}) * * X_2 (e ^ {jw})
-
Симметрия — x ^ * (n) \ Leftrightarrow X ^ * (e ^ {- j \ omega}) ;
x ^ * (- n) \ Leftrightarrow X ^ * (e ^ {j \ omega}) ;
Real [x (n)] \ Leftrightarrow X_ {even} (e ^ {j \ omega}) ;
Imag [x (n)] \ Leftrightarrow X_ {odd} (e ^ {j \ omega}) ;
x_ {even} (n) \ Leftrightarrow Real [x (e ^ {j \ omega})]] ;
x_ {odd} (n) \ Leftrightarrow Imag [x (e ^ {j \ omega})] ;
-
Теорема Парсеваля — \ sum _ {- \ infty} ^ \ infty | x_1 (n) | ^ 2 = \ frac {1} {2 \ pi} \ int _ {- \ pi} ^ {\ pi} | X_1 (e ^ {J \ Omega}) | ^ 2d \ Omega
Линейность : a_1x_1 (n) + a_2x_2 (n) \ Leftrightarrow a_1X_1 (e ^ {j \ omega}) + a_2X_2 (e ^ {j \ omega})
Сдвиг времени — x (nk) \ Leftrightarrow e ^ {- j \ omega k} .X (e ^ {j \ omega})
Обращение времени — x (-n) \ Leftrightarrow X (e ^ {- j \ omega})
Сдвиг частоты — e ^ {j \ omega _0n} x (n) \ Leftrightarrow X (e ^ {j (\ omega — \ omega _0)})
Область частот дифференцирования — nx (n) = j \ frac {d} {d \ omega} X (e ^ {j \ omega})
Свертка — x_1 (n) * x_2 (n) \ Leftrightarrow X_1 (e ^ {j \ omega}) \ times X_2 (e ^ {j \ omega})
Умножение — x_1 (n) \ times x_2 (n) \ Leftrightarrow X_1 (e ^ {j \ omega}) * X_2 (e ^ {j \ omega})
Соотношение — y_ {x_1 \ times x_2} (l) \ Leftrightarrow X_1 (e ^ {j \ omega}) \ times X_2 (e ^ {j \ omega})
Теорема модуляции — x (n) \ cos \ omega _0n = \ frac {1} {2} [X_1 (e ^ {j (\ omega + \ omega _0}) * * X_2 (e ^ {jw})
Симметрия — x ^ * (n) \ Leftrightarrow X ^ * (e ^ {- j \ omega}) ;
x ^ * (- n) \ Leftrightarrow X ^ * (e ^ {j \ omega}) ;
Real [x (n)] \ Leftrightarrow X_ {even} (e ^ {j \ omega}) ;
Imag [x (n)] \ Leftrightarrow X_ {odd} (e ^ {j \ omega}) ;
x_ {even} (n) \ Leftrightarrow Real [x (e ^ {j \ omega})]] ;
x_ {odd} (n) \ Leftrightarrow Imag [x (e ^ {j \ omega})] ;
Теорема Парсеваля — \ sum _ {- \ infty} ^ \ infty | x_1 (n) | ^ 2 = \ frac {1} {2 \ pi} \ int _ {- \ pi} ^ {\ pi} | X_1 (e ^ {J \ Omega}) | ^ 2d \ Omega
Ранее мы изучали выборку в частотной области. Обладая этими базовыми знаниями, мы производим выборку X (e ^ {j \ omega}) в частотной области, чтобы можно было сделать удобный цифровой анализ этих выборочных данных. Следовательно, ДПФ дискретизируется как во временной, так и в частотной области. С предположением x (n) = x_p (n)
Следовательно, ДПФ определяется как —
X (k) = DFT [x (n)] = X (\ frac {2 \ pi} {N} k) = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x (n) e ^ {- \ frac {j2 \ pi nk} {N}} , k = 0,1,…, N − 1 … eq (3)
И IDFT дается —
X (n) = IDFT [X (k)] = \ frac {1} {N} \ sum_ {k = 0} ^ {N-1} X (k) e ^ {\ frac {j2 \ pi nk} {N}} , n = 0,1,…., N − 1 … eq (4)
\ следовательно x (n) \ Leftrightarrow X (k)
Фактор Twiddle
Он обозначается как W_N и определяется как W_N = e ^ {- j2 \ pi / N} . Его величина всегда поддерживается на уровне единства. Фаза W_N = -2 \ pi / N . Это вектор на единичном круге и используется для удобства вычислений. Математически это может быть показано как —
W_N ^ r = W_N ^ {r \ pm N} = W_N ^ {r \ pm 2N} = …
-
Это функция r и периода N.
Рассмотрим N = 8, r = 0,1,2,3,… .14,15,16,….
\ Longleftrightarrow W_8 ^ 0 = W_8 ^ 8 = W_8 ^ {16} = … = … = W_8 ^ {32} = … = 1 = 1 \ angle 0
-
W_8 ^ 1 = W_8 ^ 9 = W_8 ^ {17} = … = … = W_8 ^ {33} = … = \ frac {1} {\ sqrt 2} = j \ frac {1} {\ sqrt 2} = 1 \ angle- \ frac {\ pi} {4}
Это функция r и периода N.
Рассмотрим N = 8, r = 0,1,2,3,… .14,15,16,….
\ Longleftrightarrow W_8 ^ 0 = W_8 ^ 8 = W_8 ^ {16} = … = … = W_8 ^ {32} = … = 1 = 1 \ angle 0
W_8 ^ 1 = W_8 ^ 9 = W_8 ^ {17} = … = … = W_8 ^ {33} = … = \ frac {1} {\ sqrt 2} = j \ frac {1} {\ sqrt 2} = 1 \ angle- \ frac {\ pi} {4}
Линейное преобразование
Давайте поймем, линейное преобразование —
Мы знаем это,
DFT (k) = DFT [x (n)] = X (\ frac {2 \ pi} {N} k) = \ sum_ {n = 0} ^ {N-1} x (n) .W_n ^ { -nk}; \ quad k = 0,1,…., N − 1
x (n) = IDFT [X (k)] = \ frac {1} {N} \ sum_ {k = 0} ^ {N-1} X (k) .W_N ^ {- nk}; \ quad n = 0,1,…., N − 1
Примечание. Вычисление DFT может быть выполнено с N 2 комплексным умножением и N (N-1) комплексным сложением.
x_N = \ begin {bmatrix} x (0) \\ x (1) \\. \\. \\ x (N-1) \ end {bmatrix} \ quad N \ quad point \ quad vector \ quad of \ четырехканальный сигнал \ quad x_N
x_N = \ begin {bmatrix} x (0) \\ x (1) \\. \\. \\ x (N-1) \ end {bmatrix} \ quad N \ quad point \ quad vector \ quad of \ четырехканальный сигнал \ quad x_N
X_N = \ begin {bmatrix} X (0) \\ X (1) \\. \\. \\ X (N-1) \ end {bmatrix} \ quad N \ quad point \ quad vector \ quad of \ четырехканальный сигнал \ quad X_N
X_N = \ begin {bmatrix} X (0) \\ X (1) \\. \\. \\ X (N-1) \ end {bmatrix} \ quad N \ quad point \ quad vector \ quad of \ четырехканальный сигнал \ quad X_N
$ \ begin {bmatrix} 1 & 1 & 1 & … & … & 1 \\ 1 & W_N & W_N ^ 2 & … & … & W_N ^ {N-1} \\. & W_N ^ 2 & W_N ^ 4 & … & … & W_N ^ {2 (N-1)} \\. \\ 1 & W_N ^ {N-1} & W_N ^ {2 (N-1) )} & … & … & W_N ^ {(N-1) (N-1)} \ end {bmatrix} $
N — точечный ДПФ в матричном члене задается как — X_N = W_Nx_N
W_N \ longmapsto Матрица линейного преобразования
Теперь \ quad x_N = W_N ^ {- 1} X_N
IDFT в матричной форме задается
x_N = \ frac {1} {N} W_N ^ * X_N
Сравнивая оба выражения x_N, \ quad W_N ^ {- 1} = \ frac {1} {N} W_N ^ * и W_N \ times W_N ^ * = N [I] _ {N \ times N}
Следовательно, W_N является матрицей линейного преобразования, ортогональной (унитарной) матрицей.
Из периодического свойства W_N и его симметричного свойства можно заключить, что W_N ^ {k + N / 2} = -W_N ^ k
Круговая симметрия
N-точечное ДПФ конечной длительности x (n) длины N≤L эквивалентно N-точечному ДПФ периодического расширения x (n), т.е. x_p (n) периода N. и x_p ( n) = \ sum_ {l = — \ infty} ^ \ infty x (n-Nl) . Теперь, если мы сместим последовательность, которая является периодической последовательностью на k единиц вправо, получается другая периодическая последовательность. Это известно как круговое смещение, и это дается,
x_p ^ \ prime (n) = x_p (nk) = \ sum_ {l = — \ infty} ^ \ infty x (nk-Nl)
Новая конечная последовательность может быть представлена как
x_p ^ \ prime (n) = \ begin {case} x_p ^ \ prime (n), & 0 \ leq n \ leq N-1 \\ 0 & В противном случае \ end {case}
Пример — Пусть x (n) = {1,2,4,3}, N = 4,
x_p ^ \ prime (n) = x (nk, по модулю \ quad N) \ эквивалент x ((nk)) _ N \ quad; ex-if \ quad k = 2i.e \ quad 2 \ quad unit \ quad right \ сдвиг в квадрате \ quad и \ quad N = 4,
Предполагаемое направление по часовой стрелке в качестве положительного направления.
Мы получили, x \ prime (n) = x ((n-2)) _ 4
x \ prime (0) = x ((- 2)) _ 4 = x (2) = 4
x \ prime (1) = x ((- 1)) _ 4 = x (3) = 3
x \ prime (2) = x ((- 2)) _ 4 = x (0) = 1
x \ prime (3) = x ((1)) _ 4 = x (1) = 2
Вывод — Круговой сдвиг N-точечной последовательности эквивалентен линейному сдвигу ее периодического расширения и наоборот.
Четко круговая последовательность — x (Nn) = x (n), \ quad 1 \ leq n \ leq N-1
iex_p (n) = x_p (-n) = x_p (Nn)
Четное сопряжение — x_p (n) = x_p ^ * (Nn)
Нечетно круговая последовательность — x (Nn) = -x (n), \ quad 1 \ leq n \ leq N-1
iex_p (n) = -x_p (-n) = -x_p (Nn)
Нечетное сопряжение — x_p (n) = -x_p ^ * (Nn)
Теперь x_p (n) = x_ {pe} + x_ {po} (n) , где,
x_ {pe} (n) = \ frac {1} {2} [x_p (n) + x_p ^ * (Nn)]
x_ {po} (n) = \ frac {1} {2} [x_p (n) -x_p ^ * (Nn)]
Для любого реального сигнала x (n), X (k) = X ^ * (Nk)
X_R (k) = X_R (Nk)
X_l (k) = -X_l (Nk)
\ angle X (k) = — \ angle X (NK)
Обращение времени — реверсивный сэмпл около 0- го сэмпла. Это дано как;
x ((- n)) _ N = x (Nn), \ quad 0 \ leq n \ leq N-1
Обратное время — это построение образцов последовательности в направлении по часовой стрелке, то есть в предполагаемом отрицательном направлении.
Некоторые другие важные свойства
Другие важные свойства IDFT x (n) \ longleftrightarrow X (k)
-
Обращение времени — x ((- n)) _ N = x (Nn) \ longleftrightarrow X ((- k)) _ N = X (Nk)
-
Круговой сдвиг времени — x ((nl)) _ N \ longleftrightarrow X (k) e ^ {j2 \ pi lk / N}
-
Сдвиг круговой частоты — x (n) e ^ {j2 \ pi ln / N} \ longleftrightarrow X ((kl)) _ N
-
Комплексные сопряженные свойства —
x ^ * (n) \ longleftrightarrow X ^ * ((- k)) _ N = X ^ * (Nk) \ quad и
x ^ * ((- n)) _ N = x ^ * (Nn) \ longleftrightarrow X ^ * (- k)
-
Умножение двух последовательностей —
x_1 (n) \ longleftrightarrow X_1 (k) \ quad и \ quad x_2 (n) \ longleftrightarrow X_2 (k)
\ следовательно x_1 (n) x_2 (n) \ longleftrightarrow X_1 (k) \ quadⓃ X_2 (k)
-
Круговая свертка — и умножение двух ДПФ
x_1 (k) \ quad Ⓝ x_2 (k) = \ sum_ {k = 0} ^ {N-1} x_1 (n) .x_2 ((mn)) _ n, \ quad m = 0,1,2 ,. …, N-1
x_1 (k) \ quad Ⓝ x_2 (k) \ longleftrightarrow X_1 (k) .X_2 (k)
-
Круговая корреляция — если x (n) \ longleftrightarrow X (k) и y (n) \ longleftrightarrow Y (k) , то существует последовательность кросс-корреляции, обозначаемая как \ bar Y_ {xy} , такая, что \ bar Y_ {xy} (l) = \ sum_ {n = 0} ^ {N-1} x (n) y ^ * ((nl)) _ N = X (k) .Y ^ * (k)
-
Теорема Парсеваля — Если x (n) \ longleftrightarrow X (k) и y (n) \ longleftrightarrow Y (k) ;
\ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x (n) y ^ * (n) = \ frac {1} {N} \ displaystyle \ sum \ limit_ {n = 0} ^ { N-1} Х (к) .Y ^ * (к)
Обращение времени — x ((- n)) _ N = x (Nn) \ longleftrightarrow X ((- k)) _ N = X (Nk)
Круговой сдвиг времени — x ((nl)) _ N \ longleftrightarrow X (k) e ^ {j2 \ pi lk / N}
Сдвиг круговой частоты — x (n) e ^ {j2 \ pi ln / N} \ longleftrightarrow X ((kl)) _ N
Комплексные сопряженные свойства —
x ^ * (n) \ longleftrightarrow X ^ * ((- k)) _ N = X ^ * (Nk) \ quad и
x ^ * ((- n)) _ N = x ^ * (Nn) \ longleftrightarrow X ^ * (- k)
Умножение двух последовательностей —
x_1 (n) \ longleftrightarrow X_1 (k) \ quad и \ quad x_2 (n) \ longleftrightarrow X_2 (k)
\ следовательно x_1 (n) x_2 (n) \ longleftrightarrow X_1 (k) \ quadⓃ X_2 (k)
Круговая свертка — и умножение двух ДПФ
x_1 (k) \ quad Ⓝ x_2 (k) = \ sum_ {k = 0} ^ {N-1} x_1 (n) .x_2 ((mn)) _ n, \ quad m = 0,1,2 ,. …, N-1
x_1 (k) \ quad Ⓝ x_2 (k) \ longleftrightarrow X_1 (k) .X_2 (k)
Круговая корреляция — если x (n) \ longleftrightarrow X (k) и y (n) \ longleftrightarrow Y (k) , то существует последовательность кросс-корреляции, обозначаемая как \ bar Y_ {xy} , такая, что \ bar Y_ {xy} (l) = \ sum_ {n = 0} ^ {N-1} x (n) y ^ * ((nl)) _ N = X (k) .Y ^ * (k)
Теорема Парсеваля — Если x (n) \ longleftrightarrow X (k) и y (n) \ longleftrightarrow Y (k) ;
\ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x (n) y ^ * (n) = \ frac {1} {N} \ displaystyle \ sum \ limit_ {n = 0} ^ { N-1} Х (к) .Y ^ * (к)
DSP — круговая свертка DFT
Давайте возьмем две последовательности конечной длительности x 1 (n) и x 2 (n), имеющие целую длину как N. Их ДПФ — X 1 (K) и X 2 (K) соответственно, что показано ниже:
X_1 (K) = \ sum_ {n = 0} ^ {N-1} x_1 (n) e ^ {\ frac {j2 \ Pi kn} {N}} \ quad k = 0,1,2 .. .N-1 X_2 (K) = \ sum_ {n = 0} ^ {N-1} x_2 (n) e ^ {\ frac {j2 \ Pi kn} {N}} \ quad k = 0 , 1,2 … N-1
Теперь мы попытаемся найти ДПФ другой последовательности x 3 (n), которая задается как X 3 (K)
X_3 (K) = X_1 (K) \ times X_2 (K)
Взяв IDFT из вышеперечисленного, мы получаем
x_3 (n) = \ frac {1} {N} \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} X_3 (K) e ^ {\ frac {j2 \ Pi kn} {N}}
Решив приведенное выше уравнение, наконец, получим
x_3 (n) = \ displaystyle \ sum \ limit_ {m = 0} ^ {N-1} x_1 (m) x_2 [((nm)) _ N] \ quad m = 0,1,2 … N- 1
| Точки сравнения | Линейная свертка | Круговая свертка |
|---|---|---|
| перевод | Линейное смещение | Круговое смещение |
| Образцы в результате свертки | N_1 + N_2-1 | Max (N_1, N_2) |
| Нахождение отклика фильтра | Возможный | Возможно с нулевым заполнением |
Методы круговой свертки
Как правило, есть два метода, которые приняты для выполнения круговой свертки, и они —
- Метод концентрических окружностей,
- Матричный метод умножения.
Метод концентрических кругов
Пусть x_1 (n) и x_2 (n) — две заданные последовательности. Для круговой свертки x_1 (n) и x_2 (n) выполняются следующие шаги:
-
Возьмите два концентрических круга. Нанесите N выборок x_1 (n) на окружность внешнего круга (сохраняя равные расстояния последовательных точек) в направлении против часовой стрелки.
-
Для построения графика x_2 (n) на внутреннем круге нанесите N выборок x_2 (n) по часовой стрелке, начиная с той же точки, что и 0- й образец x_1 (n) .
-
Умножьте соответствующие образцы на два круга и добавьте их, чтобы получить результат.
-
Вращайте внутренний круг против часовой стрелки с одним образцом за один раз.
Возьмите два концентрических круга. Нанесите N выборок x_1 (n) на окружность внешнего круга (сохраняя равные расстояния последовательных точек) в направлении против часовой стрелки.
Для построения графика x_2 (n) на внутреннем круге нанесите N выборок x_2 (n) по часовой стрелке, начиная с той же точки, что и 0- й образец x_1 (n) .
Умножьте соответствующие образцы на два круга и добавьте их, чтобы получить результат.
Вращайте внутренний круг против часовой стрелки с одним образцом за один раз.
Метод умножения матриц
Матричный метод представляет две заданные последовательности x_1 (n) и x_2 (n) в матричной форме.
-
Одна из данных последовательностей повторяется посредством кругового сдвига одного образца за раз, чтобы сформировать матрицу NXN.
-
Другая последовательность представлена в виде матрицы столбцов.
-
Умножение двух матриц дает результат круговой свертки.
Одна из данных последовательностей повторяется посредством кругового сдвига одного образца за раз, чтобы сформировать матрицу NXN.
Другая последовательность представлена в виде матрицы столбцов.
Умножение двух матриц дает результат круговой свертки.
DSP — линейная фильтрация DFT
DFT обеспечивает альтернативный подход к свертке во временной области. Он может быть использован для выполнения линейной фильтрации в частотной области.
Таким образом, Y (\ omega) = X (\ omega) .H (\ omega) \ longleftrightarrow y (n) .
Проблема в этом подходе частотной области состоит в том, что Y (\ omega) , X (\ omega) и H (\ omega) являются непрерывной функцией от ω, что бесполезно для цифровых вычислений на компьютерах. Тем не менее, DFT предоставляет выборочную версию этих сигналов для решения этой задачи.
Преимущество заключается в том, что, обладая знаниями о более быстрых методах DFT, таких как FFT, можно разработать вычислительно более эффективный алгоритм для вычислений в цифровых компьютерах по сравнению с подходом во временной области.
Рассмотрим последовательность конечной длительности, [x (n) = 0, \ quad for, n <0 \ quad и \ quad n \ geq L] (обобщенное уравнение), возбуждает линейный фильтр с импульсным откликом [h (n ) = 0, \ quad forn <0 \ quad и \ quad n \ geq M] .
x (n) y (n) output = y (n) = \ sum_ {k = 0} ^ {M-1} h (k) .x (nk)
Из анализа свертки ясно, что продолжительность y (n) составляет L + M − 1.
В частотной области,
Y (\ omega) = X (\ omega) .H (\ omega)
Теперь Y (\ omega) — это непрерывная функция от ω, и она дискретизируется на множестве дискретных частот с числом различных выборок, которые должны быть равны или превышать L + M-1 .
DFT \ quad size = N \ geq L + M-1
С \ omega = \ frac {2 \ pi} {N} k ,
Y (\ omega) = X (k) .H (k) , где k = 0,1,…., N-1
Где X (k) и H (k) — это N-точечные ДПФ x (n) и h (n) соответственно. x (n) \ & h (n) дополняются нулями вплоть до длины N. Это не будет искажать непрерывные спектры X (\ omega) и H (\ omega) . Поскольку N \ geq L + M-1 , N-точечное ДПФ выходной последовательности y (n) достаточно для представления y (n) в частотной области, и эти факты позволяют сделать вывод, что умножение N-точечных ДПФ на X (k) ) и H (k) с последующим вычислением N-точечного IDFT должны дать y (n).
Это подразумевает, что N-точечная круговая свертка x (n) и H (n) с заполнением нулями равна линейной свертке x (n) и h (n).
Таким образом, ДПФ можно использовать для линейной фильтрации.
Внимание — N всегда должно быть больше или равно L + M-1 . В противном случае эффект сглаживания повредит выходную последовательность.
DSP — DFT секционная свертка
Предположим, что входная последовательность x (n) большой длительности должна обрабатываться системой, имеющей импульсную характеристику конечной длительности, путем свертки двух последовательностей. Поскольку линейная фильтрация, выполняемая посредством DFT, включает в себя работу с блоком данных фиксированного размера, входная последовательность перед обработкой разделяется на блок данных другого фиксированного размера.
Последовательные блоки затем обрабатываются по одному, и результаты объединяются для получения чистого результата.
Поскольку свертка выполняется путем разделения длинной входной последовательности на секции с разными фиксированными размерами, она называется секционированной сверткой. Длинная входная последовательность сегментируется на блоки фиксированного размера до обработки FIR-фильтра.
Для оценки дискретной свертки используются два метода:
-
Метод перекрытия-сохранения
-
Метод перекрытия-добавления
Метод перекрытия-сохранения
Метод перекрытия-добавления
Метод сохранения с перекрытием
Сохранение с перекрытием — это традиционное название для эффективного способа оценки дискретной свертки между очень длинным сигналом x (n) и фильтром с конечной импульсной характеристикой (FIR) h (n). Ниже приведены шаги метода сохранения перекрытия —
Пусть длина блока входных данных = N = L + M-1. Следовательно, длина DFT и IDFT = N. Каждый блок данных несет точки данных M-1 предыдущего блока, за которыми следует L новых точек данных, чтобы сформировать последовательность данных длины N = L + M-1.
-
Во-первых, N-точечное ДПФ вычисляется для каждого блока данных.
-
При добавлении (L-1) нулей импульсная характеристика КИХ-фильтра увеличивается в длине, а точка DFT вычисляется и сохраняется.
-
Умножение двух N-точечных ДПФ H (k) и X m (k): Y ′ m (k) = H (k) .X m (k), где K = 0,1,2,… N-1
-
Тогда IDFT [Y ′ m ((k)] = y ′ ((n) = [y ′ m (0), y ′ m (1), y ′ m (2), ……. y ‘M (M-1), y’ m (M), ……. y ‘ m (N-1)]
(здесь N-1 = L + M-2)
-
Первые точки M-1 повреждены из-за наложения имен и, следовательно, они отбрасываются, потому что запись данных имеет длину N.
-
Последние L точек в точности совпадают в результате свертки, поэтому
y ‘ m (n) = y m (n), где n = M, M + 1,… .N-1
-
Чтобы избежать наложения, последние элементы M-1 каждой записи данных сохраняются, и эти точки переносятся на следующую запись и становятся первыми элементами M-1.
Во-первых, N-точечное ДПФ вычисляется для каждого блока данных.
При добавлении (L-1) нулей импульсная характеристика КИХ-фильтра увеличивается в длине, а точка DFT вычисляется и сохраняется.
Умножение двух N-точечных ДПФ H (k) и X m (k): Y ′ m (k) = H (k) .X m (k), где K = 0,1,2,… N-1
Тогда IDFT [Y ′ m ((k)] = y ′ ((n) = [y ′ m (0), y ′ m (1), y ′ m (2), ……. y ‘M (M-1), y’ m (M), ……. y ‘ m (N-1)]
(здесь N-1 = L + M-2)
Первые точки M-1 повреждены из-за наложения имен и, следовательно, они отбрасываются, потому что запись данных имеет длину N.
Последние L точек в точности совпадают в результате свертки, поэтому
y ‘ m (n) = y m (n), где n = M, M + 1,… .N-1
Чтобы избежать наложения, последние элементы M-1 каждой записи данных сохраняются, и эти точки переносятся на следующую запись и становятся первыми элементами M-1.
-
Результат IDFT, где избегают первых точек M-1, чтобы аннулировать псевдонимы, а оставшиеся точки L составляют желаемый результат как результат линейной свертки.
Результат IDFT, где избегают первых точек M-1, чтобы аннулировать псевдонимы, а оставшиеся точки L составляют желаемый результат как результат линейной свертки.
Метод добавления перекрытия
Ниже приведены шаги для определения дискретной свертки с использованием метода перекрытия —
Пусть размер входного блока данных равен L. Следовательно, размер DFT и IDFT: N = L + M-1
-
Каждый блок данных добавляется с нулями M-1 до последнего.
-
Вычислить N-точку DFT.
Каждый блок данных добавляется с нулями M-1 до последнего.
Вычислить N-точку DFT.
-
Умножаются два N-точечных ДПФ: Y m (k) = H (k) .X m (k), где k = 0, 1,2,…., N-1
-
IDFT [Y m (k)] создает блоки длиной N, на которые не влияет псевдоним, так как размер DFT равен N = L + M-1 и увеличивает длину последовательностей до N-точек, добавляя нули M-1 к каждому блок.
-
Последние точки M-1 каждого блока должны перекрываться и добавляться к первым точкам M-1 последующего блока.
(причина: каждый блок данных заканчивается нулями M-1)
Следовательно, этот метод известен как метод наложения-сложения. Таким образом, мы получаем —
y (n) = {y 1 (0), y 1 (1), y 1 (2), … .., y 1 (L-1), y 1 (L) + y 2 (0), y 1 (L + 1) + y 2 (1), … … .., y 1 (N-1) + y 2 (M-1), y 2 (M), … .. … … …}
Умножаются два N-точечных ДПФ: Y m (k) = H (k) .X m (k), где k = 0, 1,2,…., N-1
IDFT [Y m (k)] создает блоки длиной N, на которые не влияет псевдоним, так как размер DFT равен N = L + M-1 и увеличивает длину последовательностей до N-точек, добавляя нули M-1 к каждому блок.
Последние точки M-1 каждого блока должны перекрываться и добавляться к первым точкам M-1 последующего блока.
(причина: каждый блок данных заканчивается нулями M-1)
Следовательно, этот метод известен как метод наложения-сложения. Таким образом, мы получаем —
y (n) = {y 1 (0), y 1 (1), y 1 (2), … .., y 1 (L-1), y 1 (L) + y 2 (0), y 1 (L + 1) + y 2 (1), … … .., y 1 (N-1) + y 2 (M-1), y 2 (M), … .. … … …}
DSP — DFT дискретное косинусное преобразование
DCT (дискретное косинусное преобразование) представляет собой N-входную последовательность x (n), 0≤n≤N-1, как линейное преобразование или комбинацию комплексных экспонент. В результате коэффициенты ДПФ в целом являются сложными, даже если x (n) является действительным.
Предположим, мы пытаемся найти ортогональное преобразование, которое имеет структуру N × N, которая выражает вещественную последовательность x (n) как линейную комбинацию косинусной последовательности. Мы уже знаем это —
X (K) = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x (n) cos \ frac {2 \ Pi kn} {N} 0 \ leq k \ leq N-1
И x (n) = \ frac {1} {N} \ sum_ {k = 0} ^ {N-1} x (k) cos \ frac {2 \ Pi kn} {N} 0 \ leq k \ leq N-1
Это возможно, если N точечная последовательность x (n) вещественная и четная. Таким образом, x (n) = x (Nn), 0 \ leq n \ leq (N-1) . Полученный ДПФ сам по себе реальный и ровный. Эти вещи проясняют, что мы могли бы возможно использовать дискретное косинусное преобразование для любой N-точечной действительной последовательности, взяв 2N-точечное ДПФ «четного расширения» последовательности.
DCT, в основном, используется в обработке изображений и речи. Он также используется при сжатии изображений и речевых сигналов.
DFT [s (n)] = S (k) = \ sum_ {n = 0} ^ {2N-1} s (n) W_ {2N} ^ {nk}, \ quad, где \ quad 0 \ leq k \ leq 2N-1
S (k) = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x (n) W_ {2N} ^ {nk} + \ displaystyle \ sum \ limit_ {n = N} ^ {2N -1} x (2N-n-1) W_ {2N} ^ {nk}; \ quad, где \ quad 0 \ leq k \ leq 2N-1
\ Rightarrow S (k) = W_ {2N} ^ {- k / 2} + \ sum_ {n = 0} ^ {N-1} x (n) [W_ {2N} ^ {nk} W_ {2N} ^ {k / 2} + W_ {2N} ^ {- nk} W_ {2N} ^ {- k / 2}]; \ quad, где \ quad 0 \ leq k \ leq 2N-1
\ Rightarrow S (k) = W_ {2N} ^ {\ frac {k} {2}} \ sum_ {n = 0} ^ {N-1} x (n) \ cos [\ frac {\ pi} { N} (n + \ frac {1} {2}) k]; \ quad, где \ quad 0 \ leq k \ leq 2N-1
DCT определяется как,
V (k) = 2 \ sum_ {n = 0} ^ {N-1} x (n) \ cos [\ frac {\ pi} {2} (n + \ frac {1} {2}) k] \ quad где \ quad 0 \ leq k \ leq N-1
\ Rightarrow V (k) = W_ {2N} ^ {\ frac {k} {2}} S (k) \ quad или \ quad S (k) = W_ {2N} ^ {\ frac {k} {2 }} V (k), \ quad, где \ quad 0 \ leq k \ leq N-1
\ Rightarrow V (k) = 2R [W_ {2N} ^ {\ frac {k} {2}} \ sum_ {n = 0} ^ {N-1} x (n) W_ {2N} ^ {nk} ], \ quad где \ quad 0 \ leq k \ leq N-1
DSP — DFT Решенные Примеры
Пример 1
Проверьте теорему Парсеваля о последовательности x (n) = \ frac {1 ^ n} {4} u (n)
Решение — \ displaystyle \ sum \ limit _ {- \ infty} ^ \ infty | x_1 (n) | ^ 2 = \ frac {1} {2 \ pi} \ int _ {- \ pi} ^ {\ pi} | X_1 (е ^ {J \ Omega}) | ^ 2d \ Omega
LHS \ displaystyle \ sum \ limit _ {- \ infty} ^ \ infty | x_1 (n) | ^ 2
= \ displaystyle \ sum \ limit _ {- \ infty} ^ {\ infty} x (n) x ^ * (n)
= \ displaystyle \ sum \ limit _ {- \ infty} ^ \ infty (\ frac {1} {4}) ^ {2n} u (n) = \ frac {1} {1- \ frac {1} {16 }} = \ frac {16} {15}
RHS X (e ^ {j \ omega}) = \ frac {1} {1- \ frac {1} {4} ej \ omega} = \ frac {1} {1-0.25 \ cos \ omega + j0. 25 \ sin \ omega}
\ Longleftrightarrow X ^ * (e ^ {j \ omega}) = \ frac {1} {1-0.25 \ cos \ omega-j0.25 \ sin \ omega}
Расчет, X (e ^ {j \ omega}). X ^ * (e ^ {j \ omega})
= \ frac {1} {(1-0.25 \ cos \ omega) ^ 2 + (0.25 \ sin \ omega) ^ 2} = \ frac {1} {1.0625-0.5 \ cos \ omega}
\ frac {1} {2 \ pi} \ int _ {- \ pi} ^ {\ pi} \ frac {1} {1.0625-0.5 \ cos \ omega} d \ omega
\ frac {1} {2 \ pi} \ int _ {- \ pi} ^ {\ pi} \ frac {1} {1.0625-0.5 \ cos \ omega} d \ omega = 16/15
Мы можем видеть это, LHS = RHS. (Следовательно, доказано)
Пример 2
Вычислить N-точечную ДПФ из x (n) = 3 \ delta (n)
Решение — Мы знаем это,
X (K) = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x (n) e ^ {\ frac {j2 \ Pi kn} {N}}
= \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} 3 \ delta (n) e ^ {\ frac {j2 \ Pi kn} {N}}
= 3 \ delta (0) \ times e ^ 0 = 1
Итак, x (k) = 3,0 \ leq k \ leq N-1 … Анс.
Пример 3
Вычислить N-точечную ДПФ из x (n) = 7 (n-n_0)
Решение — Мы знаем это,
X (K) = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x (n) e ^ {\ frac {j2 \ Pi kn} {N}}
Подставляя значение x (n),
\ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} 7 \ delta (n-n_0) e ^ {- \ frac {j2 \ Pi kn} {N}}
= e ^ {- kj14 \ Pi kn_0 / N} … Ans
DSP — быстрое преобразование Фурье
В более ранних методах DFT мы видели, что вычислительная часть слишком длинная. Мы хотим уменьшить это. Это можно сделать с помощью БПФ или быстрого преобразования Фурье. Таким образом, мы можем сказать, что БПФ — это не что иное, как вычисление дискретного преобразования Фурье в алгоритмическом формате, где вычислительная часть будет уменьшена.
Основное преимущество наличия БПФ состоит в том, что с его помощью мы можем проектировать КИХ-фильтры. Математически БПФ можно записать следующим образом;
x [K] = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x [n] W_N ^ {nk}
Давайте возьмем пример, чтобы понять это лучше. Мы рассмотрели восемь точек, названных от x_0 \ quad до \ quad x_7 . Мы выберем четные члены в одной группе, а нечетные — в другой. Схематическое представление вышеупомянутого было показано ниже —
Здесь точки x 0 , x 2 , x 4 и x 6 были сгруппированы в одну категорию, и аналогично точки x 1 , x 3 , x 5 и x 7 были отнесены к другой категории. Теперь мы можем сделать их в группе из двух человек и продолжить вычисление. Теперь давайте посмотрим, как эти два подхода помогают в вычислениях.
x [k] = \ displaystyle \ sum \ limit_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limit_ {r = 0 } ^ {\ гидроразрыва {N} {2} -1} х [2г + 1] W_N ^ {(2г + 1) к}
= \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ times W_N ^ k
= G [k] + H [k] \ times W_N ^ k
Первоначально мы взяли последовательность из восьми пунктов, но позже мы разбили ее на две части G [k] и H [k]. G [k] обозначает четную часть, тогда как H [k] обозначает нечетную часть. Если мы хотим реализовать это через диаграмму, то это может быть показано ниже:
Из рисунка выше видно, что
W_8 ^ 4 = -1
W_8 ^ 5 = -W_8 ^ 1
W_8 ^ 6 = -W_8 ^ 2
W_8 ^ 7 = -W_8 ^ 3
Аналогично, окончательные значения можно записать следующим образом:
G [0] -H [0] = x [4]
G [1] -W_8 ^ 1H [1] = x [5]
G [2] -W_8 ^ 2H [2] = x [6]
G [1] -W_8 ^ 3H [3] = x [7]
Вышеуказанный периодический ряд. Недостатком этой системы является то, что K не может быть разбита за 4 балла. Теперь давайте разберем вышесказанное в дальнейшем. Мы получим структуры примерно так
пример
Рассмотрим последовательность x [n] = {2,1, -1, -3,0,1,2,1}. Рассчитать БПФ.
Решение — данная последовательность: x [n] = {2,1, -1, -3,0,1,2,1}
Расставьте термины, как показано ниже;
DSP — вычисление на месте
Такое эффективное использование памяти важно для разработки быстрого оборудования для расчета БПФ. Термин «вычисление на месте» используется для описания этого использования памяти.
Децимация во временной последовательности
В этой структуре мы представляем все точки в двоичном формате, то есть в 0 и 1. Затем мы обращаем эти структуры в обратном порядке. Последовательность, которую мы получаем после этого, называется последовательностью обращения битов. Это также известно как прореживание во временной последовательности. Расчет на месте восьмиточечного ДПФ показан в табличном формате, как показано ниже —
| ТОЧКИ | БИНАРНЫЙ ФОРМАТ | ВОССТАНОВЛЕНИЕ | ЭКВИВАЛЕНТНЫЕ ТОЧКИ |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Децимация в частотной последовательности
Помимо временной последовательности, N-точечная последовательность также может быть представлена по частоте. Давайте возьмем последовательность из четырех пунктов, чтобы понять это лучше.
Пусть последовательность будет x [0], x [1], x [2], x [3], x [4], x [5], x [6], x [7] . Сначала мы сгруппируем две точки в одну группу. Математически эта последовательность может быть записана как;
x [k] = \ sum_ {n = 0} ^ {N-1} x [n] W_N ^ {nk}
Теперь давайте создадим одну группу с порядковым номером от 0 до 3 и другую группу с последовательностью от 4 до 7. Теперь математически это может быть показано как;
\ displaystyle \ sum \ limit_ {n = 0} ^ {\ frac {N} {2} -1} x [n] W_N ^ {nk} + \ displaystyle \ sum \ limit_ {n = N / 2} ^ {N-1} х [п] W_N ^ {пк}
Заменим n на r, где r = 0, 1, 2…. (N / 2-1). Математически,
\ displaystyle \ sum \ limit_ {n = 0} ^ {\ frac {N} {2} -1} x [r] W_ {N / 2} ^ {nr}
Сначала мы берем первые четыре точки (x [0], x [1], x [2], x [3]) и пытаемся представить их математически следующим образом:
\ sum_ {n = 0} ^ 3x [n] W_8 ^ {nk} + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(n + 4) k}
= \ lbrace \ sum_ {n = 0} ^ 3x [n] + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(4) k} \ rbrace \ times W_8 ^ {nk}
теперь X [0] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4])
X [1] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) W_8 ^ {nk}
= [X [0] -X [4] + (X [1] -X [5]) W_8 ^ 1 + (X [2] -X [6]) W_8 ^ 2 + (X [3] -X [7]) W_8 ^ 3
Далее мы можем разбить его на две части, что означает, что вместо того, чтобы разбивать их как последовательность из 4 пунктов, мы можем разбить их на последовательность из 2 пунктов.
DSP — автоматизированное проектирование
КИХ-фильтры могут быть полезны при проектировании фильтров с помощью компьютера. Давайте возьмем пример и посмотрим, как это работает. Ниже приведен рисунок желаемого фильтра.
Выполняя компьютерное проектирование, мы разбиваем все непрерывные графические фигуры на дискретные значения. В определенных пределах мы разбиваем его на 64, 256 или 512 (и т. Д.) Количество частей, имеющих дискретные величины.
В приведенном выше примере мы приняли пределы от -π до + π. Мы разделили его на 256 частей. Точки могут быть представлены как H (0), H (1), … до H (256). Здесь мы применяем алгоритм IDFT, и это даст нам линейные фазовые характеристики.
Иногда нас может интересовать определенный порядок фильтров. Допустим, мы хотим реализовать данный дизайн через фильтр 9- го порядка. Итак, мы принимаем значения фильтра как h0, h1, h2… .h9. Математически это может быть показано как ниже
H (e ^ {j \ omega}) = h_0 + h_1e ^ {- j \ omega} + h_2e ^ {- 2j \ omega} + ….. + h_9e ^ {- 9j \ omega}
Там, где большое количество дислокаций, мы берем максимальные баллы.
Например, на приведенном выше рисунке наблюдается резкое падение наклона между точками B и C. Таким образом, мы пытаемся принять более дискретные значения в этой точке, но между точками C и D. существует постоянный наклон. меньшее количество дискретных значений.
Для разработки вышеупомянутого фильтра мы проходим процесс минимизации следующим образом;
H (e ^ {j \ omega1}) = h_0 + h_1e ^ {- j \ omega1} + h_2e ^ {- 2j \ omega1} + ….. + h_9e ^ {- 9j \ omega1}
H (e ^ {j \ omega2}) = h_0 + h_1e ^ {- j \ omega2} + h_2e ^ {- 2j \ omega2} + ….. + h_9e ^ {- 9j \ omega2}
Так же,
(e ^ {j \ omega1000}) = h_0 + h_1eH ^ {- j \ omega1000} h_2e ^ {- 2j \ omega1000} + ….. + h_9 + e ^ {- 9j \ omega1000}
Представляя вышеприведенное уравнение в матричной форме, имеем:
$$ \ begin {bmatrix} H (e ^ {j \ omega_1}) \\. \\. \\ H (e ^ {j \ omega_ {1000}}) \ end {bmatrix} = \ begin {bmatrix} e ^ {- j \ omega_1} & … & e ^ {- j9 \ omega_1} \\. & &. \\. & &. \\ e ^ {- j \ omega_ {1000}} & … & e ^ {j9 \ omega_ {1000}} \ end {bmatrix} \ begin {bmatrix} h_0 \\. \\. \\ h_9 \ end {bmatrix} $$
Давайте возьмем матрицу 1000 × 1 как матрицу B, матрицу 1000 × 9 как матрицу A и матрицу 9 × 1 как \ hat {h} .
Итак, для решения приведенной выше матрицы мы напишем
\ hat {h} = [A ^ TA] ^ {- 1} A ^ {T} B
= [A ^ {* T} A] ^ {- 1} A ^ {* T} B
где A * представляет собой комплексное сопряжение матрицы A.
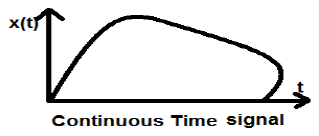
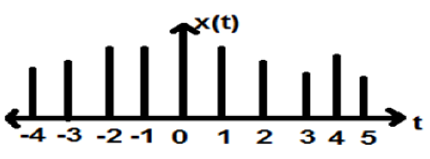
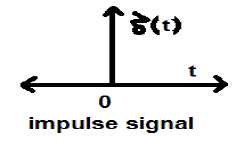
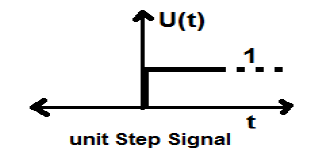
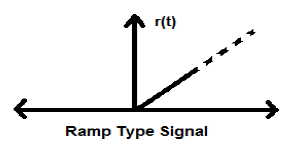
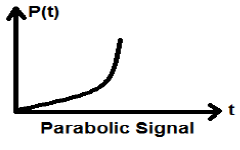
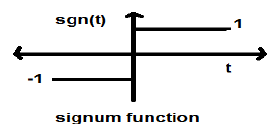
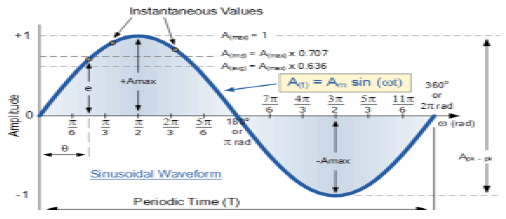
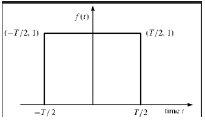
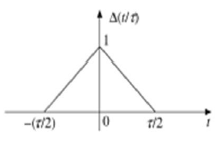
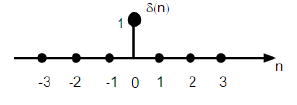
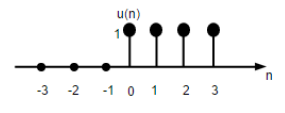
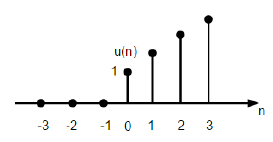
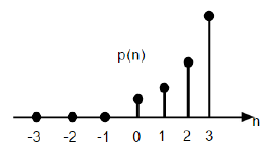
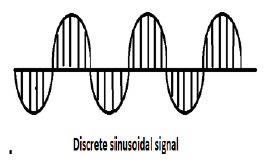
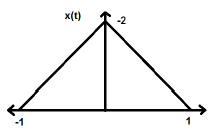
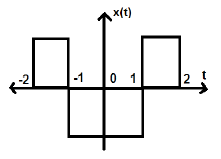
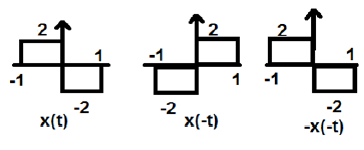
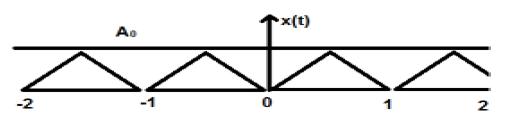
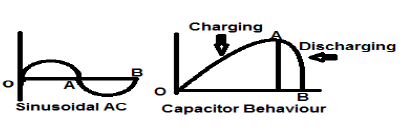
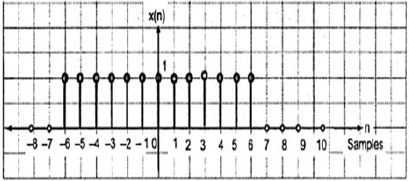
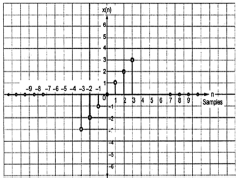
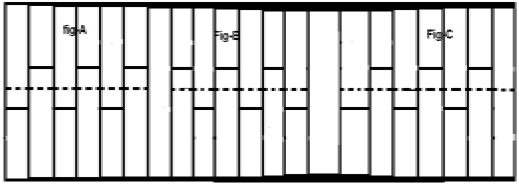
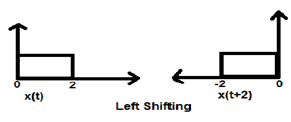
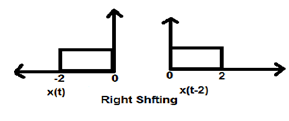
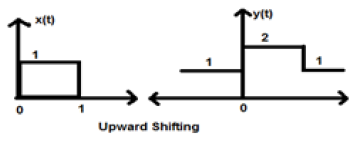
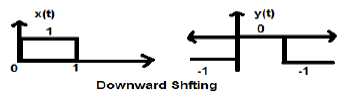
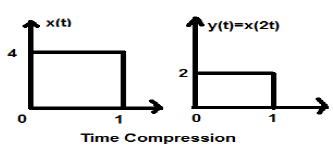
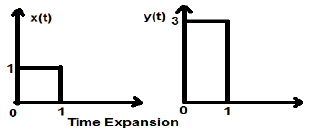
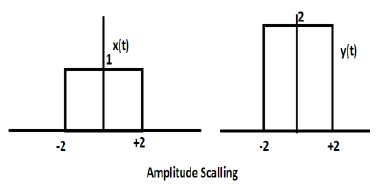
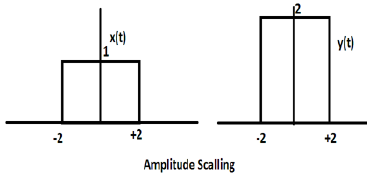
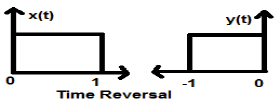
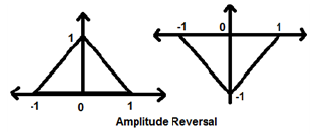
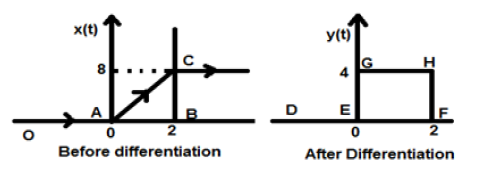
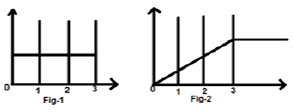
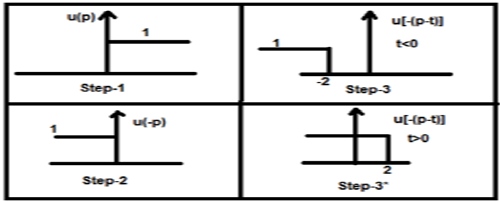
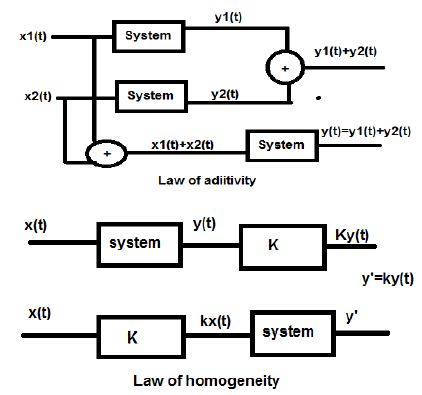
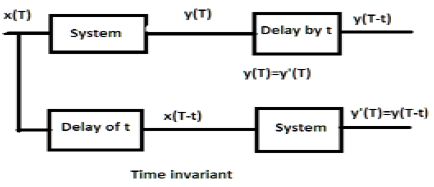
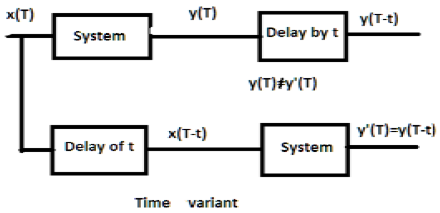
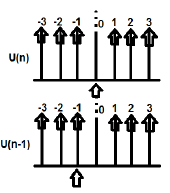
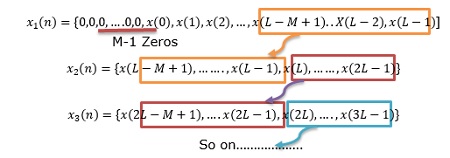

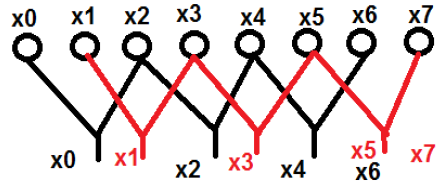
![Восемь Точек H [k] G [k] 1](/wp-content/uploads/2019/07/eight_point_h_g1-1.png)
![Восемь Точек H [k] G [k] 2](/wp-content/uploads/2019/07/eight_point_h_g2-1.png)