Мы видели, как основные сигналы могут быть представлены в непрерывной временной области. Давайте посмотрим, как основные сигналы могут быть представлены в дискретной временной области.
Последовательность импульсов
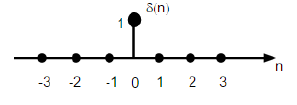
Он обозначается как δ (n) в дискретной временной области и может быть определен как;
\ delta (n) = \ begin {case} 1, & для \ quad n = 0 \\ 0, и в противном случае \ end {case}
Сигнал шага блока
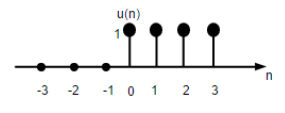
Сигнал шага дискретной единицы времени определяется как;
U (n) = \ begin {case} 1, & для \ quad n \ geq0 \\ 0, & для \ quad n <0 \ end {case}
На рисунке выше показано графическое представление дискретной функции шага.
Функция рампы
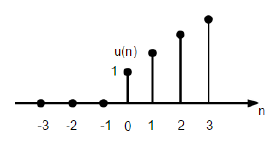
Дискретная функция линейного изменения может быть определена как —
r (n) = \ begin {case} n, & для \ quad n \ geq0 \\ 0, & для \ quad n <0 \ end {case}
На приведенном выше рисунке показано графическое представление дискретного сигнала линейного изменения.
Параболическая функция
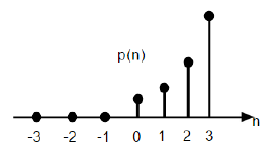
Дискретная единица параболической функции обозначается как p (n) и может быть определена как;
p (n) = \ begin {case} \ frac {n ^ {2}} {2}, & для \ quad n \ geq0 \\ 0, & для \ quad n <0 \ end {case}
С точки зрения функции единичного шага это может быть записано как;
P(n)= fracn22U(n)
На приведенном выше рисунке показано графическое представление параболической последовательности.
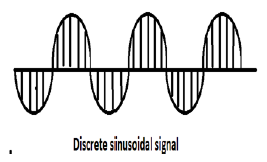
Синусоидальный сигнал
Все непрерывные сигналы являются периодическими. Синусоидальные последовательности с дискретным временем могут быть или не быть периодическими. Они зависят от значения ω. Чтобы дискретный сигнал времени был периодическим, угловая частота ω должна быть рациональным кратным 2π.
Дискретный синусоидальный сигнал показан на рисунке выше.
Дискретная форма синусоидального сигнала может быть представлена в формате —
x(n)=A sin( omegan+ phi)
Здесь A, ω и φ имеют свое обычное значение, а n — целое число. Период времени дискретного синусоидального сигнала определяется как —
N= frac2 pim omega
Где N и m — целые числа