DSP — Операции по интеграции сигналов

Интеграция любого сигнала означает суммирование этого сигнала в определенной временной области для получения модифицированного сигнала. Математически это можно представить как —

x(t) rightarrowy(t)= intt− inftyx(t)dt

$$x (t) \ rightarrow y (t) = \ int _ {- \ infty} ^ {t} x (t) dt$$

Здесь также, в большинстве случаев, мы можем выполнить математическое интегрирование и найти полученный сигнал, но прямое интегрирование в быстрой последовательности возможно для сигналов, которые графически представлены в прямоугольном формате. Как и дифференцирование, здесь мы также будем ссылаться на таблицу, чтобы быстро получить результат.

пример

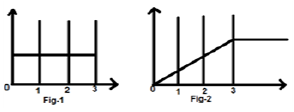
Рассмотрим сигнал x(t)=u(t)−u(t−3)$x (t) = u (t) -u (t-3)$. Это показано на фиг.1-1 ниже. Ясно, что мы видим, что это шаговый сигнал. Теперь мы интегрируем это. Обращаясь к таблице, мы знаем, что интегрирование сигнала шага дает сигнал линейного изменения.

Тем не менее, мы рассчитаем это математически,

y(t)= intt− inftyx(t)dt$y (t) = \ int _ {- \ infty} ^ {t} x (t) dt$

= intt− infty[u(t)−u(t−3)]dt$= \ int _ {- \ infty} ^ {t} [u (t) -u (t-3)] dt$

= intt− inftyu(t)dt− intt− inftyu(t−3)dt$= \ int _ {- \ infty} ^ {t} u (t) dt- \ int _ {- \ infty} ^ {t} u (t-3) dt$

=r(t)−r(t−3)$= r (t) -r (t-3)$

То же самое, как показано на рис-2,