DSP — быстрое преобразование Фурье

В более ранних методах DFT мы видели, что вычислительная часть слишком длинная. Мы хотим уменьшить это. Это можно сделать с помощью БПФ или быстрого преобразования Фурье. Таким образом, мы можем сказать, что БПФ — это не что иное, как вычисление дискретного преобразования Фурье в алгоритмическом формате, где вычислительная часть будет уменьшена.

Основное преимущество наличия БПФ состоит в том, что с его помощью мы можем проектировать КИХ-фильтры. Математически БПФ можно записать следующим образом;

$$x [K] = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x [n] W_N ^ {nk}$$

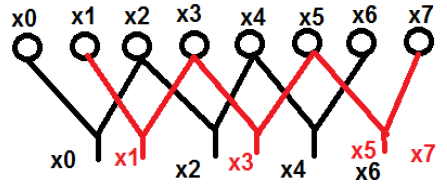
Давайте возьмем пример, чтобы понять это лучше. Мы рассмотрели восемь точек, названных от $x_0 \ quad до \ quad x_7$. Мы выберем четные члены в одной группе, а нечетные — в другой. Схематическое представление вышеупомянутого было показано ниже —

Здесь точки x ₀ , x ₂ , x ₄ и x ₆ были сгруппированы в одну категорию, и аналогично точки x ₁ , x ₃ , x ₅ и x ₇ были отнесены к другой категории. Теперь мы можем сделать их в группе из двух человек и продолжить вычисление. Теперь давайте посмотрим, как эти два подхода помогают в вычислениях.

$x [k] = \ displaystyle \ sum \ limit_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limit_ {r = 0 } ^ {\ гидроразрыва {N} {2} -1} х [2г + 1] W_N ^ {(2г + 1) к}$

$= \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ times W_N ^ k$

$= G [k] + H [k] \ times W_N ^ k$

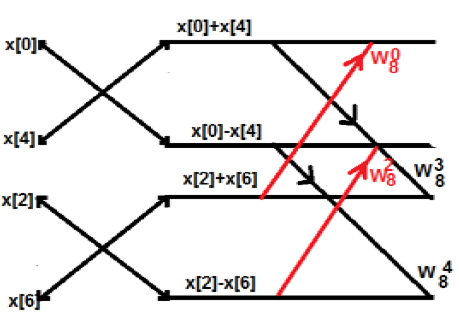
Первоначально мы взяли последовательность из восьми пунктов, но позже мы разбили ее на две части G [k] и H [k]. G [k] обозначает четную часть, тогда как H [k] обозначает нечетную часть. Если мы хотим реализовать это через диаграмму, то это может быть показано ниже:

Из рисунка выше видно, что

$W_8 ^ 4 = -1$

$W_8 ^ 5 = -W_8 ^ 1$

$W_8 ^ 6 = -W_8 ^ 2$

$W_8 ^ 7 = -W_8 ^ 3$

Аналогично, окончательные значения можно записать следующим образом:

$G [0] -H [0] = x [4]$

$G [1] -W_8 ^ 1H [1] = x [5]$

$G [2] -W_8 ^ 2H [2] = x [6]$

$G [1] -W_8 ^ 3H [3] = x [7]$

Вышеуказанный периодический ряд. Недостатком этой системы является то, что K не может быть разбита за 4 балла. Теперь давайте разберем вышесказанное в дальнейшем. Мы получим структуры примерно так

пример

Рассмотрим последовательность x [n] = {2,1, -1, -3,0,1,2,1}. Рассчитать БПФ.

Решение — данная последовательность: x [n] = {2,1, -1, -3,0,1,2,1}

Расставьте термины, как показано ниже;