Строительство корневого локуса

Корневой локус является графическим представлением в s-области, и он симметричен относительно действительной оси. Потому что полюсы и нули в разомкнутом контуре существуют в s-области, имеющей значения в виде вещественных или комплексных сопряженных пар. В этой главе давайте обсудим, как построить (нарисовать) корневой локус.

Правила построения корневого локуса

Следуйте этим правилам для построения корневого локуса.

Правило 1 — Найдите полюсы и нули разомкнутой петли в плоскости ‘s’.

Правило 2 — Найти количество ветвей корневых локусов.

Мы знаем, что ветви корневых локусов начинаются на полюсах разомкнутого контура и заканчиваются на нулях разомкнутого контура. Таким образом, число ветвей корневых локусов N равно числу конечных полюсов разомкнутой петли P или числу конечных нулей разомкнутой петли Z , в зависимости от того, что больше.

Математически мы можем записать число корневых ветвей локуса N как

$N = P$, если $P \ geq Z$

$N = Z$, если $P <Z$

Правило 3 — Определите и нарисуйте ветви корневых локусов реальной оси .

Если угол передаточной функции разомкнутого контура в точке нечетно кратен 180 ⁰ , то эта точка находится в корневом локусе. Если нечетное число полюсов и нулей разомкнутой петли существует слева от точки на действительной оси, то эта точка находится на ветви корневого локуса. Следовательно, ветвь точек, которая удовлетворяет этому условию, является действительной осью ветви корневого локуса.

Правило 4 — Найдите центроид и угол асимптоты.

• Если $P = Z$, то все ветви корневых локусов начинаются с конечных полюсов разомкнутой петли и заканчиваются конечными нулями разомкнутой петли.

• Если $P> Z$, то число корневых локусных ветвей $Z$ начинается с конечных полюсов разомкнутой петли и заканчивается в нулях конечной разомкнутой петли, а число корневых локусных ветвей $P - Z$ начинается с конечных полюсов разомкнутой петли и заканчивается на бесконечных нули с разомкнутым контуром.

• Если $P <Z$, то число корневых локусных ветвей P начинается с конечных полюсов разомкнутой петли и заканчивается на конечных нулях разомкнутой петли, а число Z — P $ корневых ветвей локуса начинается с бесконечных полюсов разомкнутой петли и заканчивается в конечной разомкнутой петле нули.

Если $P = Z$, то все ветви корневых локусов начинаются с конечных полюсов разомкнутой петли и заканчиваются конечными нулями разомкнутой петли.

Если $P> Z$, то число корневых локусных ветвей $Z$ начинается с конечных полюсов разомкнутой петли и заканчивается в нулях конечной разомкнутой петли, а число корневых локусных ветвей $P - Z$ начинается с конечных полюсов разомкнутой петли и заканчивается на бесконечных нули с разомкнутым контуром.

Если $P <Z$, то число корневых локусных ветвей P начинается с конечных полюсов разомкнутой петли и заканчивается на конечных нулях разомкнутой петли, а число Z — P $ корневых ветвей локуса начинается с бесконечных полюсов разомкнутой петли и заканчивается в конечной разомкнутой петле нули.

Итак, некоторые ветви корневых локусов приближаются к бесконечности, когда $P \ neq Z$. Асимптоты указывают направление ветвей корневых локусов. Точка пересечения асимптот на реальной оси называется центроидом .

Мы можем рассчитать центроид α , используя эту формулу,

 alpha= frac sumRealpartofконечныйopenlooppoles− sumRealpartofofконечныйopenloop :нулиPZ$\ alpha = \ frac {\ sum Real \: part \: of \: конечный \: open \: loop \: poles \: - \ sum Real \: part \: of \: of \: конечный \: open \: loop \ : нули} {PZ}$

Формула для угла асимптот θ имеет вид

$$\ тета = \ гидроразрыва {(2q + 1), 180 ^ 0} {PZ}$$

Куда,

$$д = 0,1,2, ...., (ПЗ) -1$$

Правило 5 — Найдите точки пересечения ветвей корневых локусов с мнимой осью.

Мы можем вычислить точку, в которой корневая ветвь локуса пересекает мнимую ось и значение K в этой точке, используя метод массива Рауса и специальный случай (ii) .

• Если все элементы какой-либо строки массива Рауса равны нулю, тогда корневая ветвь локуса пересекает мнимую ось и наоборот.

• Определите строку таким образом, что если мы сделаем первый элемент нулевым, то элементы всей строки будут равны нулю. Найдите значение K для этой комбинации.

• Подставьте это значение K во вспомогательное уравнение. Вы получите точку пересечения ветви корневого локуса с мнимой осью.

Если все элементы какой-либо строки массива Рауса равны нулю, тогда корневая ветвь локуса пересекает мнимую ось и наоборот.

Определите строку таким образом, что если мы сделаем первый элемент нулевым, то элементы всей строки будут равны нулю. Найдите значение K для этой комбинации.

Подставьте это значение K во вспомогательное уравнение. Вы получите точку пересечения ветви корневого локуса с мнимой осью.

Правило 6 — Найти точки отрыва и взлома.

• Если между двумя полюсами разомкнутого контура существует ветвь корневого локуса реальной оси, то между этими двумя полюсами разомкнутого контура будет точка отрыва .

• Если между двумя нулями разомкнутого контура существует ветвь корневого локуса действительной оси, то между этими двумя нулями разомкнутого контура будет точка разрыва .

Если между двумя полюсами разомкнутого контура существует ветвь корневого локуса реальной оси, то между этими двумя полюсами разомкнутого контура будет точка отрыва .

Если между двумя нулями разомкнутого контура существует ветвь корневого локуса действительной оси, то между этими двумя нулями разомкнутого контура будет точка разрыва .

Примечание. Точки отрыва и взлома существуют только на ветвях корневых локусов реальной оси.

Выполните следующие действия, чтобы найти точки отрыва и взлома.

• Запишите $K$ в терминах $s$ из характеристического уравнения $1 + G (s) H (s) = 0$.

• Продифференцируйте $K$ по s и сделайте его равным нулю. Подставьте эти значения $s$ в приведенном выше уравнении.

• Значения $s$, для которых значение $K$ является положительным, являются точками разрыва .

Запишите $K$ в терминах $s$ из характеристического уравнения $1 + G (s) H (s) = 0$.

Продифференцируйте $K$ по s и сделайте его равным нулю. Подставьте эти значения $s$ в приведенном выше уравнении.

Значения $s$, для которых значение $K$ является положительным, являются точками разрыва .

Правило 7 — Найдите угол вылета и угол прибытия.

Угол вылета и угол прихода могут быть рассчитаны для комплексных сопряженных полюсов разомкнутой петли и комплексных сопряженных нулей разомкнутой петли соответственно.

Формула для угла вылета $\ phi_d$:

$$\ phi_d = 180 ^ 0- \ Phi$$

Формула для угла прихода $\ phi_a$:

$$\ phi_a = 180 ^ 0 + \ Phi$$

Куда,

$$\ phi = \ sum \ phi_P- \ sum \ phi_Z$$

пример

Теперь нарисуем корневой локус системы управления, имеющей передаточную функцию с разомкнутым контуром, $G (s) H (s) = \ frac {K} {s (s + 1) (s + 5)}$

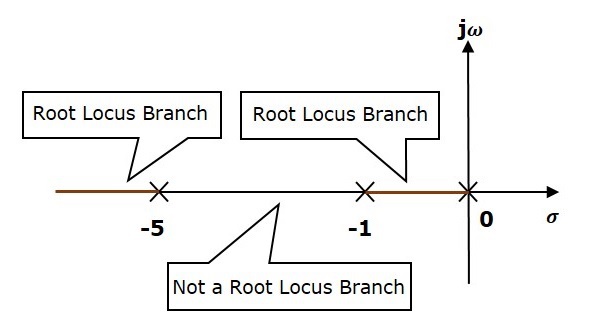
Шаг 1 — Данная передаточная функция с разомкнутым контуром имеет три полюса при $s = 0, s = −1$ и $s = −5$. У него нет нуля. Следовательно, число ветвей корневых локусов равно числу полюсов передаточной функции разомкнутого контура.

$$N = Р = 3$$

Три полюса расположены, как показано на рисунке выше. Сегмент прямой между $s = −1$ и $s = 0$ является одной ветвью корневого локуса на действительной оси. А другая ветвь корневого локуса на действительной оси — это отрезок слева от $s = −5$.

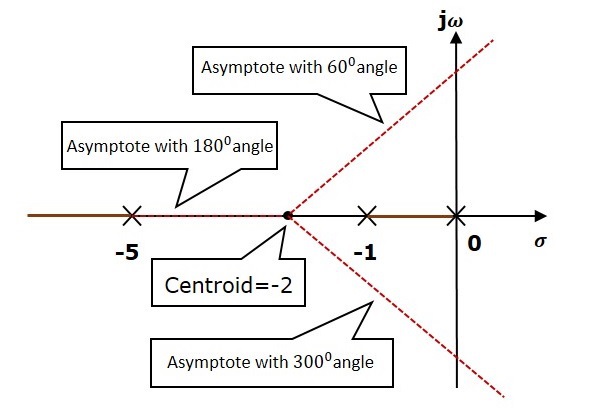
Шаг 2 — Мы получим значения центроида и угла асимптоты, используя данные формулы.

Центроид $\ alpha = −2$

Угол асимптоты составляет $\ theta = 60 ^ 0,180 ^ 0$ и $300 ^ 0$.

Центроид и три асимптоты показаны на следующем рисунке.

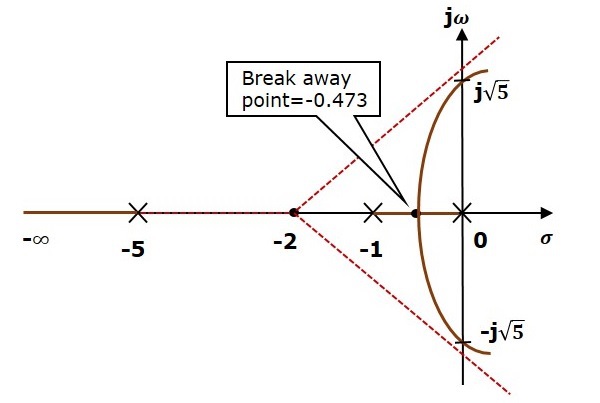
Шаг 3 — Поскольку две асимптоты имеют углы $60 ^ 0$ и $300 ^ 0$, две ветви корневых локусов пересекают мнимую ось. Используя метод массива Рауса и особый случай (ii), ветви корневых локусов пересекают мнимую ось в $j \ sqrt {5}$ и $−j \ sqrt {5}$.

Будет одна точка отрыва на ветви корневого локуса реальной оси между полюсами $s = −1$ и $s = 0$. Следуя процедуре, данной для расчета точки отрыва, мы получим ее как $s = −0,473$.

Диаграмма корневого локуса для данной системы управления показана на следующем рисунке.

Таким образом, вы можете нарисовать диаграмму корневого локуса любой системы управления и наблюдать за перемещением полюсов передаточной функции замкнутого контура.

Из диаграмм корневых локусов мы можем узнать диапазон значений K для различных типов демпфирования.

Эффекты добавления полюсов и нулей с открытой петлей на корневой локус

Корневой локус может быть сдвинут в плоскости ‘s’ путем добавления полюсов разомкнутого контура и нулей разомкнутого контура.

• Если мы включим полюс в передаточную функцию разомкнутого контура, то некоторые ветви корневого локуса будут двигаться к правой половине плоскости ‘s’. Из-за этого коэффициент демпфирования $\ delta$ уменьшается. Это означает, что демпфированная частота $\ omega_d$ увеличивается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, уменьшаются. Но это влияет на стабильность системы.

• Если мы включим ноль в передаточную функцию разомкнутого контура, то некоторые ветви корневых локусов переместятся к левой половине плоскости ‘s’. Таким образом, это повысит стабильность системы управления. В этом случае коэффициент демпфирования $\ delta$ увеличивается. Это означает, что демпфированная частота $\ omega_d$ уменьшается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, увеличиваются.

Если мы включим полюс в передаточную функцию разомкнутого контура, то некоторые ветви корневого локуса будут двигаться к правой половине плоскости ‘s’. Из-за этого коэффициент демпфирования $\ delta$ уменьшается. Это означает, что демпфированная частота $\ omega_d$ увеличивается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, уменьшаются. Но это влияет на стабильность системы.

Если мы включим ноль в передаточную функцию разомкнутого контура, то некоторые ветви корневых локусов переместятся к левой половине плоскости ‘s’. Таким образом, это повысит стабильность системы управления. В этом случае коэффициент демпфирования $\ delta$ увеличивается. Это означает, что демпфированная частота $\ omega_d$ уменьшается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, увеличиваются.

Таким образом, основываясь на требовании, мы можем включить (добавить) полюсы или нули разомкнутого контура в передаточную функцию.