Ответ системы второго порядка

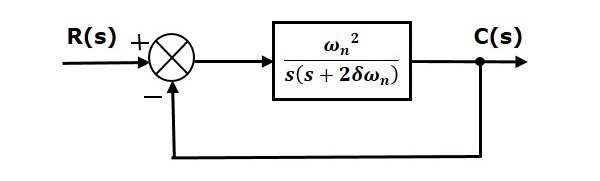
В этой главе давайте обсудим временную характеристику системы второго порядка. Рассмотрим следующую блок-схему замкнутой системы управления. Здесь передаточная функция с разомкнутым контуром, $\ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)}$, связана с единственной отрицательной обратной связью.

Известно, что передаточная функция замкнутой системы управления, имеющей единичную отрицательную обратную связь, равна

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {G (s)} {1 + G (s)}$$

Замените $G (s) = \ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)}$ в вышеприведенном уравнении.

$$\ frac {C (s)} {R (s)} = \ frac {\ left (\ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)} \ right)} {1+ \ left (\ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)} \ right)} = \ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega _ns + \ omega _n ^ 2}$$

Сила ‘s’ — это два в знаменателе. Следовательно, вышеупомянутая передаточная функция имеет второй порядок, и система называется системой второго порядка .

Характеристическое уравнение —

$$s ^ 2 + 2 \ delta \ omega _ns + \ omega _n ^ 2 = 0$$

Корни характеристического уравнения —

$$s = \ frac {-2 \ omega \ delta _n \ pm \ sqrt {(2 \ delta \ omega _n) ^ 2-4 \ omega _n ^ 2}} {2} = \ frac {-2 (\ delta \ omega _n \ pm \ omega _n \ sqrt {\ delta ^ 2-1})} {2}$$

$$\ Rightarrow s = - \ delta \ omega_n \ pm \ omega _n \ sqrt {\ delta ^ 2-1}$$

• Два корня мнимые, когда δ = 0.
• Два корня действительны и равны, когда δ = 1.
• Два корня действительны, но не равны, когда δ> 1.
• Два корня являются комплексно сопряженными, когда 0 <δ <1.

Мы можем написать уравнение $C (s)$ как,

$$C (s) = \ left (\ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2} \ right) R (s)$$

Куда,

• C (s) — преобразование Лапласа выходного сигнала, c (t)

• R (s) — преобразование Лапласа входного сигнала, r (t)

• ω _n — собственная частота

• δ — коэффициент демпфирования.

C (s) — преобразование Лапласа выходного сигнала, c (t)

R (s) — преобразование Лапласа входного сигнала, r (t)

ω _n — собственная частота

δ — коэффициент демпфирования.

Выполните следующие действия, чтобы получить ответ (вывод) системы второго порядка во временной области.

• Возьмем преобразование Лапласа входного сигнала, $r (t)$.

• Рассмотрим уравнение, $C (s) = \ left (\ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2} \ right) R (s)$

• Замените значение $R (s)$ в приведенном выше уравнении.

• Делайте частичные дроби $C (s)$, если требуется.

• Примените обратное преобразование Лапласа к $C (s)$.

Возьмем преобразование Лапласа входного сигнала, $r (t)$.

Рассмотрим уравнение, $C (s) = \ left (\ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2} \ right) R (s)$

Замените значение $R (s)$ в приведенном выше уравнении.

Делайте частичные дроби $C (s)$, если требуется.

Примените обратное преобразование Лапласа к $C (s)$.

Шаговая реакция системы второго порядка

Рассмотрим сигнал единичного шага в качестве входа в систему второго порядка.

Преобразование Лапласа единичного сигнала шага,

$$R (s) = \ гидроразрыва {1} {s}$$

Мы знаем, что передаточная функция замкнутой системы управления второго порядка:

$$\ frac {C (s)} {R (s)} = \ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2}$$

Случай 1: δ = 0

Подставьте $\ delta = 0$ в передаточную функцию.

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {s ^ 2 + \ omega_n ^ 2}$$

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {s ^ 2 + \ omega_n ^ 2} \ right) R (s)$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {\ omega_n ^ 2} {s ^ 2 + \ omega_n ^ 2} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s (s ^ 2 + \ omega_n ^ 2)}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (1- \ cos (\ omega_n t) \ right) u (t)$$

Таким образом, отклик единичного шага системы второго порядка, когда $/ delta = 0$, будет непрерывным сигналом времени с постоянной амплитудой и частотой.

Случай 2: δ = 1

Замените $/ delta = 1$ в передаточной функции.

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {s ^ 2 + 2 \ omega_ns + \ omega_n ^ 2}$$

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ omega_n) ^ 2} \ right) R (s)$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ omega_n) ^ 2} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s (s + \ omega_n) ^ 2}$$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {\ omega_n ^ 2} {S (S + \ omega_n) ^ 2} = \ гидроразрыва {A}, {s} + \ гидроразрыва {B}, {S + \ omega_n} + \ гидроразрыва {С } {(s + \ omega_n) ^ 2}$$

После упрощения вы получите значения A, B и C как 1,−1и− omegan$1, \: -1 \: и \: - \ omega _n$ соответственно. Подставьте эти значения в приведенное выше частичное дробное выражение $C (s)$.

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {1} {S + \ omega_n} - \ гидроразрыва {\ omega_n} {(з + \ omega_n) ^ 2}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = (1-e ^ {- \ omega_nt} - \ omega _nte ^ {- \ omega_nt}) u (t)$$

Таким образом, единичный шаговый отклик системы второго порядка будет пытаться достичь пошагового ввода в устойчивом состоянии.

Случай 3: 0 <δ <1

Мы можем изменить знаменатель члена передаточной функции следующим образом:

$$s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2 = \ left \ {s ^ 2 + 2 (s) (\ delta \ omega_n) + (\ delta \ omega_n) ^ 2 \ right \} + \ omega_n ^ 2 - (\ Delta \ omega_n) ^ 2$$

$$= (S + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)$$

Передаточная функция становится,

$$ \ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)} $ $

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2)} \ right) R (s )$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$ C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2)} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s \ left ((s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2) \ right)} $ $

Делаем частичные дроби $C (s)$.

$$C (s) = \ frac {\ omega_n ^ 2} {s \ left ((s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2) \ right)} = \ frac { А} {s} + \ гидроразрыва {Bs + С} {(s + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)}$$

После упрощения вы получите значения A, B и C как 1,−1и−2 delta omegan$1, \: -1 \: и \: −2 \ delta \ omega _n$ соответственно. Подставьте эти значения в приведенное выше частичное расширение доли C (s).

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {S + 2 \ дельта \ omega_n} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2) }$$

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {S + \ дельта \ omega_n} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)} - \ гидроразрыва {\ Delta \ omega_n} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)}$$

$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {(S + \ дельта \ omega_n)} {(з + \ дельта \ omega_n) ^ 2 + (\ omega_n \ SQRT {1- \ дельта ^ 2} ) ^ 2} - \ frac {\ delta} {\ sqrt {1- \ delta ^ 2}} \ left (\ frac {\ omega_n \ sqrt {1- \ delta ^ 2}}} ((s + \ delta \ omega_n) ^ 2 + (\ omega_n \ sqrt {1- \ delta ^ 2}) ^ 2} \ right)$

Замените $\ omega_n \ sqrt {1- \ delta ^ 2}$ на $\ omega_d$ в вышеприведенном уравнении.

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {(S + \ дельта \ omega_n)} {(з + \ дельта \ omega_n) ^ 2 + \ omega_d ^ 2} - \ гидроразрыва {\ Delta} {\ sqrt {1- \ delta ^ 2}} \ left (\ frac {\ omega_d} {(s + \ delta \ omega_n) ^ 2 + \ omega_d ^ 2} \ right)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (1-e ^ {- \ delta \ omega_nt} \ cos (\ omega_dt) - \ frac {\ delta} {\ sqrt {1- \ delta ^ 2}} e ^ {- \ delta \ omega_nt} \ sin (\ omega_dt) \ right) u (t)$$

$$c (t) = \ left (1- \ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ left ((\ sqrt {1- \ delta ^ 2 }) \ cos (\ omega_dt) + \ delta \ sin (\ omega_dt) \ right) \ right) u (t)$$

Если $\ sqrt {1- \ delta ^ 2} = \ sin (\ theta)$, то δ будет cos (θ). Подставьте эти значения в приведенное выше уравнение.

$$c (t) = \ left (1- \ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} (\ sin (\ theta) \ cos (\ omega_dt) + \ cos (\ theta) \ sin (\ omega_dt)) \ right) u (t)$$

$$\ Rightarrow c (t) = \ left (1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta) \ right) u (t)$$

Таким образом, отклик единичного шага системы второго порядка имеет затухающие колебания (уменьшение амплитуды), когда «δ» лежит между нулем и единицей.

Случай 4: δ> 1

Мы можем изменить знаменатель члена передаточной функции следующим образом:

$$s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2 = \ left \ {s ^ 2 + 2 (s) (\ delta \ omega_n) + (\ delta \ omega_n) ^ 2 \ right \} + \ omega_n ^ 2 - (\ Delta \ omega_n) ^ 2$$

$$= \ left (s + \ delta \ omega_n \ right) ^ 2- \ omega_n ^ 2 \ left (\ delta ^ 2-1 \ right)$$

Передаточная функция становится,

$$ \ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {(з + \ дельта \ omega_n) ^ 2- \ omega_n ^ 2 (\ дельта ^ 2-1)} $ $

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2- \ omega_n ^ 2 (\ delta ^ 2-1)} \ right) R (s) )$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2 - (\ omega_n \ sqrt {\ delta ^ 2-1}) ^ 2} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s (s + \ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}) (s + \ delta \ omega_n- \ omega_n \ SQRT {\ Delta ^ 2-1})}$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {\ omega_n ^ 2} {S (S + \ дельта \ omega_n + \ omega_n \ SQRT {\ Delta ^ 2-1}) (S + \ Delta \ omega_n- \ omega_n \ SQRT {\ дельта ^ 2-1})}$$

$$= \ гидроразрыва {A}, {s} + \ гидроразрыва {B}, {S + \ дельта \ omega_n + \ omega_n \ SQRT {\ Delta ^ 2-1}} + \ гидроразрыва {C}, {S + \ Delta \ omega_n- \ omega_n \ SQRT {\ Delta ^ 2-1}}$$

После упрощения вы получите значения A, B и C как 1, $\ frac {1} {2 (\ delta + \ sqrt {\ delta ^ 2-1}) (\ sqrt {\ delta ^ 2-1} )}$ и $\ frac {-1} {2 (\ delta- \ sqrt {\ delta ^ 2-1}) (\ sqrt {\ delta ^ 2-1})}$ соответственно. Подставьте эти значения в приведенное выше частичное дробное разложение $C (s)$.

$$C (S) = \ гидроразрыва {1} {s} + \ гидроразрыва {1} {2 (\ Delta + \ SQRT {\ Delta ^ 2-1}) (\ SQRT {\ Delta ^ 2-1})} \ left (\ frac {1} {s + \ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}} \ right) - \ left (\ frac {1} {2 (\ delta- \ sqrt {\ delta) ^ 2-1}) (\ sqrt {\ delta ^ 2-1})} \ right) \ left (\ frac {1} {s + \ delta \ omega_n- \ omega_n \ sqrt {\ delta ^ 2-1}} \ право)$$

Примените обратное преобразование Лапласа с обеих сторон.

$c (t) = \ left (1+ \ left (\ frac {1} {2 (\ delta + \ sqrt {\ delta ^ 2-1}) (\ sqrt {\ delta ^ 2-1})}} right ) e ^ {- (\ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}) t} - \ left (\ frac {1} {2 (\ delta- \ sqrt {\ delta ^ 2-1} ) (\ sqrt {\ delta ^ 2-1})} \ right) e ^ {- (\ delta \ omega_n- \ omega_n \ sqrt {\ delta ^ 2-1}) t} \ right) u (t)$

Поскольку он слишком демпфирован, отклик единичного шага системы второго порядка, когда δ> 1, никогда не достигнет шага ввода в установившемся режиме.

Импульсный отклик системы второго порядка

Импульсная характеристика системы второго порядка может быть получена с помощью любого из этих двух методов.

• При получении ответа на шаг следуйте процедуре, рассматривая значение $R (s)$ как 1 вместо $\ frac {1} {s}$.

• Сделайте дифференциацию шага ответа.

При получении ответа на шаг следуйте процедуре, рассматривая значение $R (s)$ как 1 вместо $\ frac {1} {s}$.

Сделайте дифференциацию шага ответа.

В следующей таблице приведены импульсные характеристики системы второго порядка для 4 случаев коэффициента демпфирования.

δ = 0

$\ Omega_n \ sin (\ omega_nt)$

δ = 1

$\ Omega_n ^ 2TE ^ {- \ omega_nt}$

0 <δ <1

$\ left (\ frac {\ omega_ne ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt)$

δ> 1

$\ left (\ frac {\ omega_n} {2 \ sqrt {\ delta ^ 2-1}} \ right) \ left (e ^ {- (\ delta \ omega_n- \ omega_n \ sqrt {\ delta ^ 2-1) }) t} -e ^ {- (\ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}) t} \ right)$