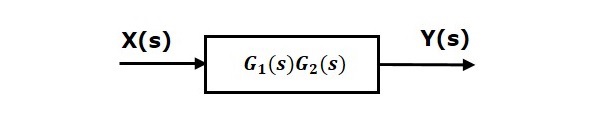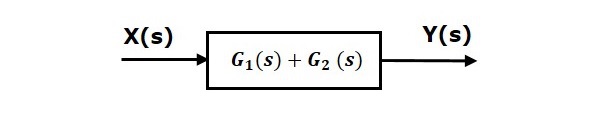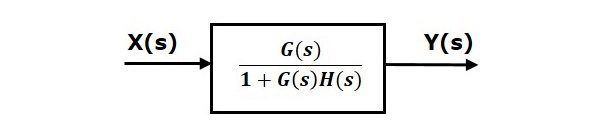Системы управления — блок-схема алгебры

Алгебра блок-схем — это не что иное, как алгебра, связанная с основными элементами блок-диаграммы. Эта алгебра имеет дело с графическим представлением алгебраических уравнений.

Основные соединения для блоков

Существует три основных типа соединений между двумя блоками.

Последовательное соединение

Последовательное соединение также называется каскадным соединением . На следующем рисунке два блока, имеющие передаточные функции $G_1 (s)$ и $G_2 (s)$, соединены последовательно.

Для этой комбинации мы получим вывод $Y (s)$ как

$$Y (s) = G_2 (ы) Z (S)$$

Где $Z (s) = G_1 (s) X (s)$

$$\ Rightarrow Y (s) = G_2 (s) [G_1 (s) X (s)] = G_1 (s) G_2 (s) X (s)$$

$$\ Rightarrow Y (s) = \ lbrace G_1 (s) G_2 (s) \ rbrace X (s)$$

Сравните это уравнение со стандартной формой выходного уравнения, $Y (s) = G (s) X (s)$. Где $G (s) = G_1 (s) G_2 (s)$.

Это означает, что мы можем представить последовательное соединение двух блоков одним блоком. Передаточная функция этого единственного блока является произведением передаточных функций этих двух блоков. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить последовательное соединение n блоков с одним блоком. Передаточная функция этого единственного блока является произведением передаточных функций всех этих «n» блоков.

Параллельное соединение

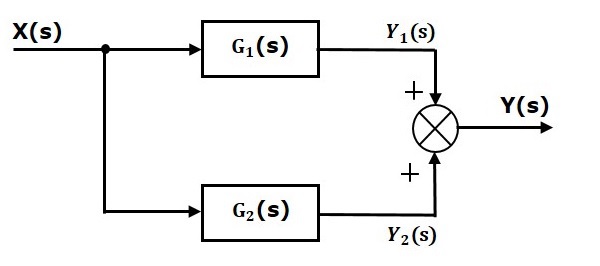
Блоки, которые соединены параллельно, будут иметь одинаковый вход . На следующем рисунке два блока, имеющие передаточные функции $G_1 (s)$ и $G_2 (s)$, соединены параллельно. Выходы этих двух блоков подключены к точке суммирования.

Для этой комбинации мы получим вывод $Y (s)$ как

$$Y (s) = Y_1 (тв) + Y_2 (ы)$$

Где $Y_1 (s) = G_1 (s) X (s)$ и $Y_2 (s) = G_2 (s) X (s)$

$$\ Rightarrow Y (s) = G_1 (s) X (s) + G_2 (s) X (s) = \ lbrace G_1 (s) + G_2 (s) \ rbrace X (s)$$

Сравните это уравнение со стандартной формой выходного уравнения, $Y (s) = G (s) X (s)$.

Где $G (s) = G_1 (s) + G_2 (s)$.

Это означает, что мы можем представить параллельное соединение двух блоков с одним блоком. Передаточная функция этого единственного блока является суммой передаточных функций этих двух блоков. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить параллельное соединение n блоков с одним блоком. Передаточная функция этого единственного блока является алгебраической суммой передаточных функций всех этих «n» блоков.

Обратная связь

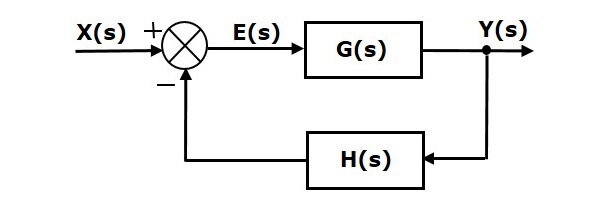
Как мы уже говорили в предыдущих главах, существует два типа обратной связи — положительная и отрицательная. На следующем рисунке показана система контроля отрицательной обратной связи. Здесь два блока с передаточными функциями $G (s)$ и $H (s)$ образуют замкнутый цикл.

Выход точки суммирования —

$$E (S) = X (S) -H (ы) Y (ы)$$

Выход $Y (s)$ —

$$Y (s) = Е (ы) О (ы)$$

Замените значение $E (s)$ в приведенном выше уравнении.

$$Y (s) = \ left \ {X (s) -H (s) Y (s) \ rbrace G (s) \ right \}$$

$$Y (s) \ left \ {1 + G (s) H (s) \ rbrace = X (s) G (s) \ right \}$$

$$\ Rightarrow \ frac {Y (s)} {X (s)} = \ frac {G (s)} {1 + G (s) H (s)}$$

Следовательно, передаточная функция замкнутого контура с отрицательной обратной связью равна $\ frac {G (s)} {1 + G (s) H (s)}$

Это означает, что мы можем представить соединение отрицательной обратной связи двух блоков с одним блоком. Передаточная функция этого одиночного блока является передаточной функцией обратной связи с обратной связью. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить соединение положительного отклика двух блоков с одним блоком. Передаточная функция этого единственного блока является передаточной функцией замкнутого контура положительной обратной связи, т. Е. $\ Frac {G (s)} {1-G (s) H (s)}$

Блок-схема алгебры суммирования баллов

Есть две возможности смещения точек суммирования относительно блоков —

• Смещение точки суммирования после блока
• Смещение точки суммирования перед блоком

Давайте теперь посмотрим, какие меры необходимо предпринять в вышеупомянутых двух случаях один за другим.

Смещение точки суммирования после блока

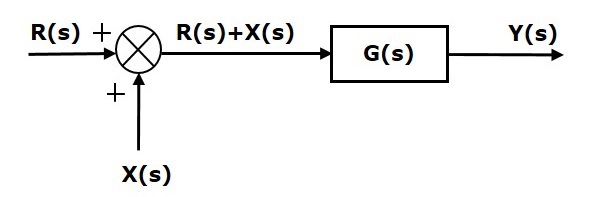
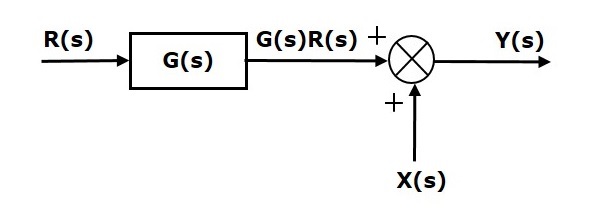
Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка суммирования присутствует перед блоком.

Точка суммирования имеет два входа $R (s)$ и $X (s)$. Выходные данные: $\ left \ {R (s) + X (s) \ right \}$.

Таким образом, вход в блок $G (s)$ равен $\ left \ {R (s) + X (s) \ right \}$, а его выход —

$$Y (s) = G (s) \ left \ {R (s) + X (s) \ right \}$$

$\ Rightarrow Y (s) = G (s) R (s) + G (s) X (s)$ (Уравнение 1)

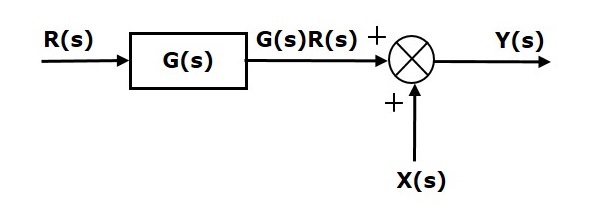
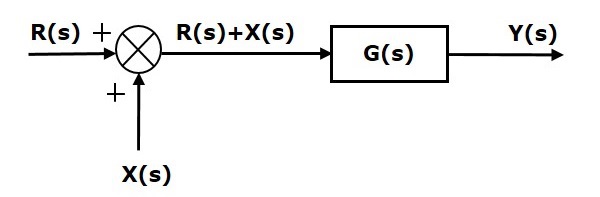
Теперь сдвиньте точку суммирования после блока. Эта блок-схема показана на следующем рисунке.

Выход блока $G (s)$ равен $G (s) R (s)$.

Выход точки суммирования

$Y (s) = G (s) R (s) + X (s)$ (уравнение 2)

Сравните уравнение 1 и уравнение 2.

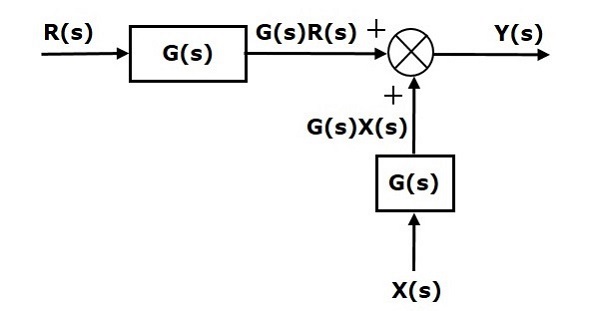
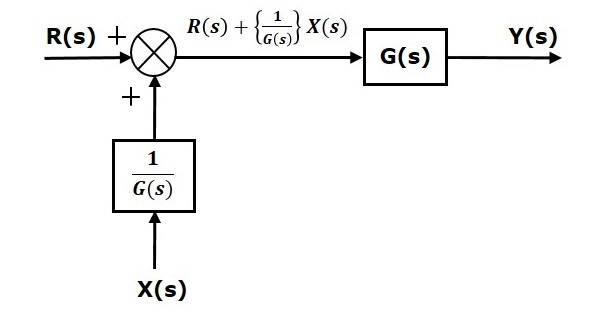
Первое слагаемое ′G(s)R(s)′$'G (s) R (s)'$ одинаково в обоих уравнениях. Но есть разница во втором семестре. Чтобы получить второй член, такой же, нам нужен еще один блок $G (s)$. Он имеет входные данные $X (s)$, а выходные данные этого блока задаются в качестве входных данных для точки суммирования вместо $X (s)$. Эта блок-схема показана на следующем рисунке.

Смещение точки суммирования перед блоком

Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка суммирования присутствует после блока.

Выход этой блок-схемы —

$Y (s) = G (s) R (s) + X (s)$ (уравнение 3)

Теперь сдвиньте точку суммирования перед блоком. Эта блок-схема показана на следующем рисунке.

Выход этой блок-схемы —

$Y (S) = G (s) R (s) + G (s) X (s)$ (Уравнение 4)

Сравните уравнение 3 и уравнение 4,

Первое слагаемое ′G(s)R(s)′$'G (s) R (s)'$ одинаково в обоих уравнениях. Но есть разница во втором семестре. Чтобы получить второй член, такой же, нам нужен еще один блок $\ frac {1} {G (s)}$. Он имеет входные данные $X (s)$, а выходные данные этого блока задаются в качестве входных данных для точки суммирования вместо $X (s)$. Эта блок-схема показана на следующем рисунке.

Алгебра блок-схем для точек взлета

Есть две возможности сдвига точек взлета относительно блоков —

• Сдвиг точки взлета после блока
• Сдвиг точки взлета перед блоком

Давайте теперь посмотрим, какие меры должны быть предприняты в вышеупомянутых двух случаях, один за другим.

Сдвиг точки взлета после блока

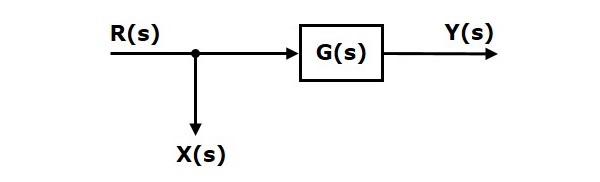
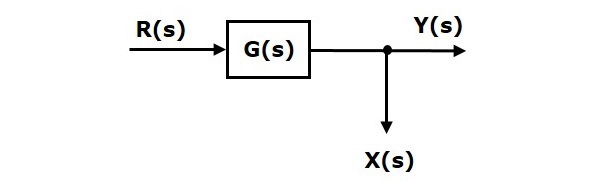
Рассмотрим блок-схему, показанную на следующем рисунке. В этом случае точка взлета присутствует перед блоком.

Здесь $X (s) = R (s)$ и $Y (s) = G (s) R (s)$

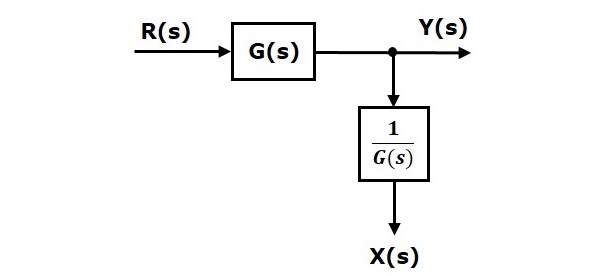
Когда вы сдвигаете точку взлета после блока, выходные данные $Y (s)$ будут такими же. Но есть разница в значении $X (s)$. Итак, чтобы получить то же значение $X (s)$, нам потребуется еще один блок $\ frac {1} {G (s)}$. Он имеет вход $Y (s)$, а вывод — $X (s)$. Эта блок-схема показана на следующем рисунке.

Сдвиг точки взлета перед блоком

Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка взлета присутствует после блока.

Здесь $X (s) = Y (s) = G (s) R (s)$

Когда вы сдвигаете точку взлета перед блоком, выходные данные $Y (s)$ будут такими же. Но есть разница в значении $X (s)$. Итак, чтобы получить то же значение $X (s)$, нам потребуется еще один блок $G (s)$. Он имеет вход $R (s)$, а вывод — $X (s)$. Эта блок-схема показана на следующем рисунке.