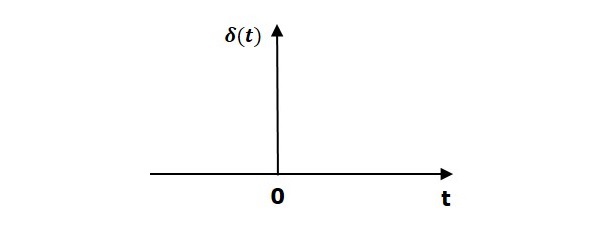Мы можем проанализировать реакцию систем управления как во временной, так и в частотной областях. Мы обсудим анализ частотных характеристик систем управления в следующих главах. Давайте теперь обсудим анализ времени отклика систем управления.
Что такое время отклика?
Если выходной сигнал системы управления для входа изменяется во времени, то он называется временной реакцией системы управления. Время отклика состоит из двух частей.
- Переходный ответ
- Устойчивый государственный ответ
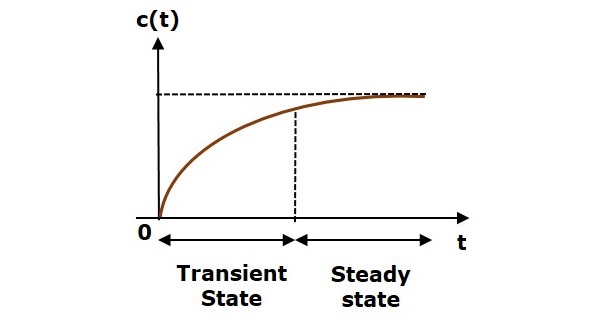
Реакция системы управления во временной области показана на следующем рисунке.
Здесь как переходные, так и стационарные состояния указаны на рисунке. Ответы, соответствующие этим состояниям, известны как ответы переходного и стационарного состояний.
Математически мы можем записать временную характеристику c (t) как
C(T)=Cтр(т)+Cсс(т)
Куда,
- c tr (t) — переходный ответ
- c ss (t) — реакция устойчивого состояния
Переходный ответ
После подачи ввода в систему управления, выходу требуется определенное время для достижения устойчивого состояния. Таким образом, выходной сигнал будет в переходном состоянии, пока он не перейдет в устойчивое состояние. Следовательно, ответ системы управления во время переходного состояния называется переходным процессом .
Переходный отклик будет нулевым для больших значений «t». В идеале это значение ‘t’ равно бесконечности и практически в пять раз больше.
Математически мы можем записать это как
limt rightarrow inftyctr(t)=0
Устойчивый государственный ответ
Часть временного отклика, которая остается даже после переходного отклика, имеет нулевое значение для больших значений «t», называется устойчивым откликом . Это означает, что переходный отклик будет нулевым даже в установившемся режиме.
пример
Найдем нестационарные и установившиеся состояния временной реакции системы управления c(t)=10+5e−t
Здесь второе слагаемое 5e−t будет равно нулю, так как t обозначает бесконечность. Итак, это переходный термин . И первый член 10 остается даже при приближении t к бесконечности. Итак, это термин устойчивого состояния .
Стандартные тестовые сигналы
Стандартные тестовые сигналы: импульсный, шаговый, линейный и параболический. Эти сигналы используются для определения производительности систем управления с использованием временной характеристики выхода.
Импульсный сигнал блока
Единичный импульсный сигнал δ (t) определяется как
delta(t)=0 для t neq0
и int0+0− delta(t)dt=1
На следующем рисунке показан единичный импульсный сигнал.
Итак, единичный импульсный сигнал существует только при ‘t’, равном нулю. Площадь этого сигнала при небольшом интервале времени вокруг ‘t’ равна нулю и равна единице. Значение единичного импульсного сигнала равно нулю для всех остальных значений «t».
Сигнал шага блока
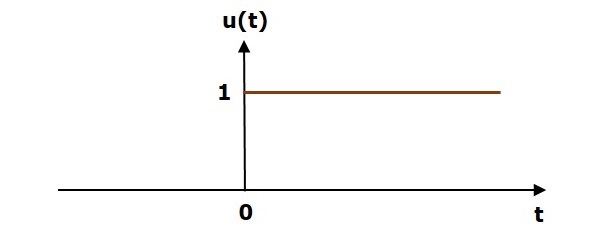
Единичный шаговый сигнал u (t) определяется как
u(t)=1;t geq0
$ = 0; т <0 $
На следующем рисунке показан сигнал шага блока.
Таким образом, сигнал единичного шага существует для всех положительных значений ‘t’, включая ноль. И его значение равно единице за этот интервал. Значение сигнала единичного шага равно нулю для всех отрицательных значений ‘t’.
Сигнал рампы
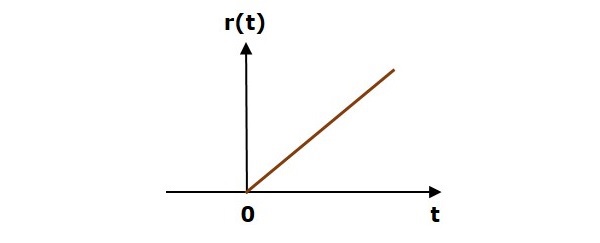
Сигнал линейного изменения r (t) определяется как
$$ R (T) = т; t \ geq 0 $$
$ = 0; т <0 $
Мы можем записать единичный сигнал линейного изменения, r(t) через единичный сигнал шага, u(t) как
R(T)=TU(T)
На следующем рисунке показан сигнал линейного изменения.
Таким образом, сигнал линейного изменения существует для всех положительных значений ‘t’, включая ноль. И его значение увеличивается линейно по отношению к ‘t’ в течение этого интервала. Значение единичного сигнала линейного изменения равно нулю для всех отрицательных значений ‘t’.
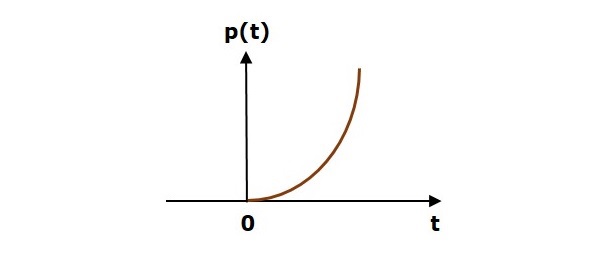
Единичный параболический сигнал
Единичный параболический сигнал p (t) определяется как,
$$ р (т) = \ гидроразрыва {т ^ 2} {2}; t \ geq 0 $$
$ = 0; т <0 $
Мы можем записать единичный параболический сигнал, p(t) через единичный сигнал шага, u(t) как,
р(т)= гидроразрыват22и(т)
На следующем рисунке показан блок параболического сигнала.
Таким образом, единичный параболический сигнал существует для всех положительных значений ‘t’, включая ноль. И его значение увеличивается нелинейно по отношению к ‘t’ в течение этого интервала. Значение единичного параболического сигнала равно нулю для всех отрицательных значений ‘t’.