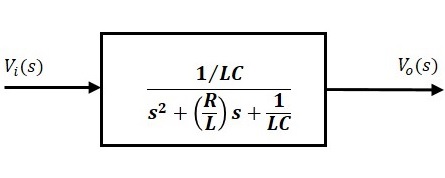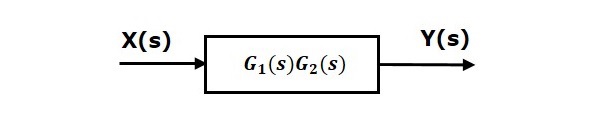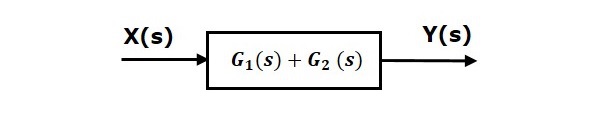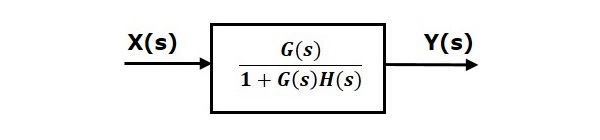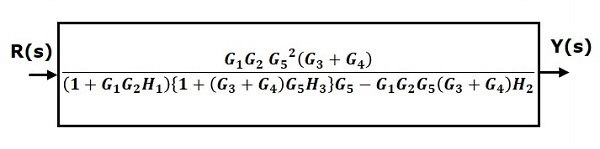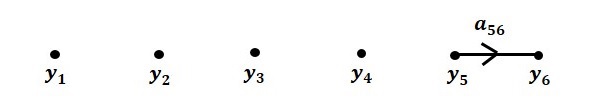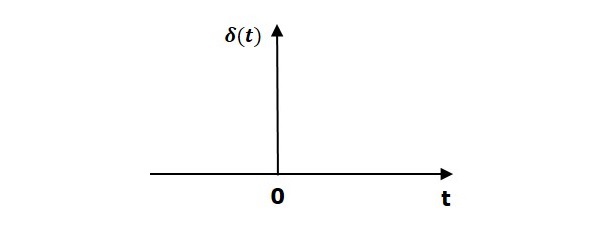Системы управления — Введение

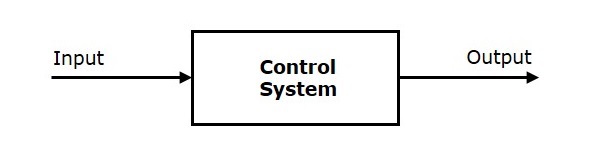
Система управления — это система, которая обеспечивает желаемый ответ путем управления выходом. На следующем рисунке показана простая блок-схема системы управления.

Здесь система управления представлена ​​единым блоком. Поскольку выход управляется переменным входом, система управления получила это название. Мы будем варьировать этот вход с некоторым механизмом. В следующем разделе, посвященном системам управления с разомкнутым и замкнутым контуром, мы подробно изучим блоки внутри системы управления и способы изменения этого входа для получения желаемого отклика.

Примеры — Система управления светофорами, стиральная машина

Система управления светофорами является примером системы управления. Здесь последовательность входного сигнала применяется к этой системе управления, и выход является одним из трех источников света, которые будут включены в течение некоторого времени. В течение этого времени два других индикатора будут выключены. На основании исследования движения на конкретном перекрестке можно определить время включения и выключения света. Соответственно, входной сигнал управляет выходом. Итак, система управления светофорами работает по расписанию.

Классификация систем управления

На основании некоторых параметров мы можем классифицировать системы управления следующими способами.

Системы непрерывного и дискретного времени

• Системы управления могут быть классифицированы как системы непрерывного контроля времени и системы дискретного контроля времени, основанные на типе используемого сигнала .

• В системах непрерывного контроля времени все сигналы непрерывны во времени. Но в системах управления с дискретным временем существует один или несколько сигналов с дискретным временем.

Системы управления могут быть классифицированы как системы непрерывного контроля времени и системы дискретного контроля времени, основанные на типе используемого сигнала .

В системах непрерывного контроля времени все сигналы непрерывны во времени. Но в системах управления с дискретным временем существует один или несколько сигналов с дискретным временем.

Системы управления SISO и MIMO

• Системы управления могут быть классифицированы как системы управления SISO и системы управления MIMO по количеству имеющихся входов и выходов .

• Системы управления SISO (с одним входом и одним выходом) имеют один вход и один выход. Принимая во внимание, что системы управления MIMO (несколько входов и несколько выходов) имеют более одного входа и более одного выхода.

Системы управления могут быть классифицированы как системы управления SISO и системы управления MIMO по количеству имеющихся входов и выходов .

Системы управления SISO (с одним входом и одним выходом) имеют один вход и один выход. Принимая во внимание, что системы управления MIMO (несколько входов и несколько выходов) имеют более одного входа и более одного выхода.

Системы управления с открытым и закрытым контуром

Системы управления могут быть классифицированы как системы управления с обратной связью и системы управления с обратной связью на основе пути обратной связи .

В системах управления с разомкнутым контуром выход не передается на вход. Таким образом, управляющее действие не зависит от желаемого результата.

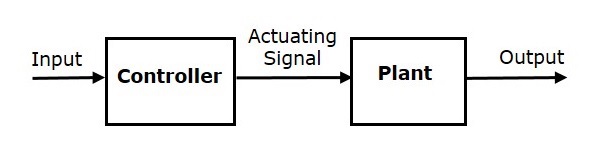
На следующем рисунке показана блок-схема системы управления без обратной связи.

Здесь вход подается на контроллер, и он генерирует управляющий сигнал или управляющий сигнал. Этот сигнал подается в качестве входа на установку или процесс, который необходимо контролировать. Таким образом, завод производит продукцию, которая контролируется. Система управления светофорами, о которой мы говорили ранее, является примером системы управления без обратной связи.

В системах управления с обратной связью выход подается обратно на вход. Таким образом, управляющее действие зависит от желаемого выхода.

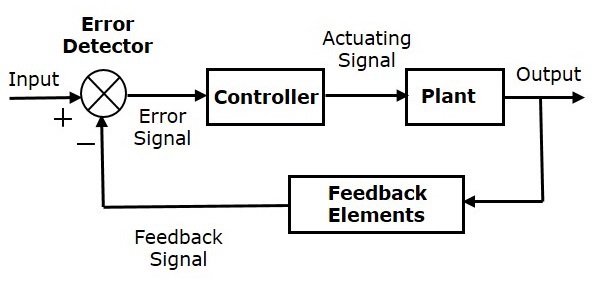
На следующем рисунке показана блок-схема системы управления с обратной связью с обратной связью.

Детектор ошибок выдает сигнал ошибки, который представляет собой разницу между входным сигналом и сигналом обратной связи. Этот сигнал обратной связи получают из блока (элементов обратной связи), рассматривая выходные данные всей системы в качестве входных данных для этого блока. Вместо прямого входа сигнал ошибки подается в качестве входа в контроллер.

Таким образом, контроллер выдает исполнительный сигнал, который контролирует установку. В этой комбинации выход системы управления корректируется автоматически, пока мы не получим желаемый ответ. Следовательно, замкнутые системы управления также называются системами автоматического управления. Система управления светофорами, имеющая датчик на входе, является примером системы управления с обратной связью.

Различия между системами управления с разомкнутым и замкнутым контуром упомянуты в следующей таблице.

Системы управления с открытым контуром	Системы управления замкнутым контуром
Управляющее действие не зависит от желаемого выхода.	Управляющее действие зависит от желаемого выхода.
Путь обратной связи отсутствует.	Путь обратной связи присутствует.
Они также называются системами управления без обратной связи .	Они также называются системами управления с обратной связью .
Легко оформить.	Сложно оформить.
Это экономно.	Это дороже.
Неточный.	Точная.

Системы управления — Обратная связь

Если вывод или некоторая часть вывода возвращаются на сторону ввода и используются как часть ввода системы, то это называется обратной связью . Обратная связь играет важную роль в повышении производительности систем управления. В этой главе давайте обсудим типы обратной связи и ее влияние.

Типы отзывов

Есть два типа обратной связи —

• Положительный отзыв
• Негативный отзыв

Положительный отзыв

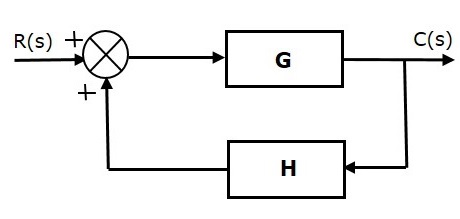
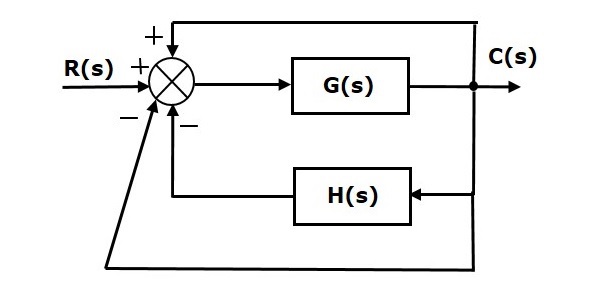
Положительная обратная связь добавляет опорный вход, $R (s)$ и вывод обратной связи. На следующем рисунке показана блок-схема системы управления положительной обратной связью .

Концепция передаточной функции будет обсуждаться в следующих главах. В настоящее время рассмотрим передаточную функцию системы управления положительной обратной связью,

$T = \ frac {G} {1-GH}$ (Уравнение 1)

Куда,

• Т — передаточная функция или общее усиление системы управления положительной обратной связью.

• G — коэффициент усиления без обратной связи, который является функцией частоты.

• H — коэффициент усиления обратной связи, который является функцией частоты.

Т — передаточная функция или общее усиление системы управления положительной обратной связью.

G — коэффициент усиления без обратной связи, который является функцией частоты.

H — коэффициент усиления обратной связи, который является функцией частоты.

Негативный отзыв

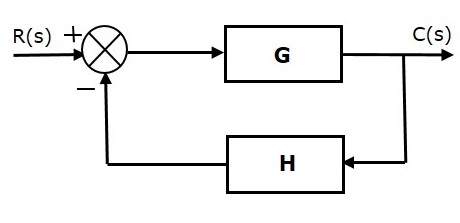
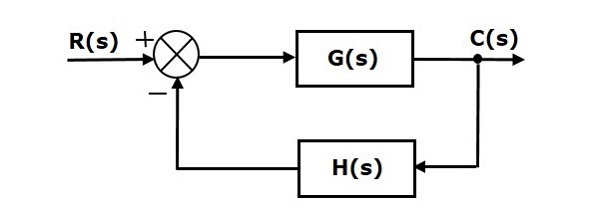
Отрицательная обратная связь уменьшает ошибку между опорным входом, $R (s)$ и выходом системы. На следующем рисунке показана блок-схема системы управления отрицательной обратной связью .

Передаточная функция системы управления отрицательной обратной связью,

$T = \ frac {G} {1 + GH}$ (уравнение 2)

Куда,

• Т — передаточная функция или общий коэффициент усиления системы управления с отрицательной обратной связью.

• G — коэффициент усиления без обратной связи, который является функцией частоты.

• H — коэффициент усиления обратной связи, который является функцией частоты.

Т — передаточная функция или общий коэффициент усиления системы управления с отрицательной обратной связью.

G — коэффициент усиления без обратной связи, который является функцией частоты.

H — коэффициент усиления обратной связи, который является функцией частоты.

Вывод вышеупомянутой передаточной функции представлен в следующих главах.

Эффекты обратной связи

Давайте теперь поймем эффект обратной связи.

Влияние обратной связи на общий доход

• Из уравнения 2 можно сказать, что общий выигрыш в системе управления с обратной связью с отрицательной обратной связью представляет собой отношение «G» и (1 + GH). Таким образом, общее усиление может увеличиваться или уменьшаться в зависимости от значения (1 + GH).

• Если значение (1 + GH) меньше 1, общий коэффициент усиления увеличивается. В этом случае значение «GH» является отрицательным, поскольку усиление пути обратной связи является отрицательным.

• Если значение (1 + GH) больше 1, то общее усиление уменьшается. В этом случае значение «GH» является положительным, поскольку усиление пути обратной связи является положительным.

Из уравнения 2 можно сказать, что общий выигрыш в системе управления с обратной связью с отрицательной обратной связью представляет собой отношение «G» и (1 + GH). Таким образом, общее усиление может увеличиваться или уменьшаться в зависимости от значения (1 + GH).

Если значение (1 + GH) меньше 1, общий коэффициент усиления увеличивается. В этом случае значение «GH» является отрицательным, поскольку усиление пути обратной связи является отрицательным.

Если значение (1 + GH) больше 1, то общее усиление уменьшается. В этом случае значение «GH» является положительным, поскольку усиление пути обратной связи является положительным.

В общем, «G» и «H» являются функциями частоты. Таким образом, обратная связь увеличит общее усиление системы в одном частотном диапазоне и уменьшит в другом частотном диапазоне.

Влияние обратной связи на чувствительность

Чувствительность общего усиления отрицательной обратной связи системы управления замкнутого контура ( T ) к изменению усиления разомкнутого контура ( G ) определяется как

STG= frac frac частичныйTT frac частичныйGG= fracПроцентизменитьвTPercentagechangeinG$S_ {G} ^ {T} = \ frac {\ frac {\ частичный T} {T}} {\ frac {\ частичный G} {G}} = \ frac {Процент \: изменить \: в \: T } {Percentage \: change \: in \: G}$ (уравнение 3)

Где, ∂T — инкрементное изменение T из-за инкрементного изменения G.

Мы можем переписать уравнение 3 как

$S_ {G} ^ {T} = \ frac {\ частичный T} {\ частичный G} \ frac {G} {T}$ (уравнение 4)

Делаем частичное дифференцирование по G с обеих сторон уравнения 2.

$\ frac {\ частичный T} {\ частичный G} = \ frac {\ частный} {\ частичный G} \ left (\ frac {G} {1 + GH} \ right) = \ frac {(1 + GH) .1-G (H)} {(1 + GH) ^ 2} = \ frac {1} {(1 + GH) ^ 2}$ (уравнение 5)

Из уравнения 2 вы получите

$\ frac {G} {T} = 1 + GH$ (Уравнение 6)

Замените уравнение 5 и уравнение 6 на уравнение 4.

$$S_ {G} ^ {Т} = \ гидроразрыва {1} {(1 + GH) ^ 2} (1 + GH) = \ гидроразрыва {1} {1 + GH}$$

Таким образом, мы получили чувствительность общего усиления системы управления с обратной связью как обратную величину (1 + GH). Таким образом, чувствительность может увеличиваться или уменьшаться в зависимости от значения (1 + GH).

• Если значение (1 + GH) меньше 1, чувствительность увеличивается. В этом случае значение «GH» является отрицательным, поскольку усиление канала обратной связи является отрицательным.

• Если значение (1 + GH) больше 1, чувствительность уменьшается. В этом случае значение «GH» является положительным, поскольку усиление пути обратной связи является положительным.

Если значение (1 + GH) меньше 1, чувствительность увеличивается. В этом случае значение «GH» является отрицательным, поскольку усиление канала обратной связи является отрицательным.

Если значение (1 + GH) больше 1, чувствительность уменьшается. В этом случае значение «GH» является положительным, поскольку усиление пути обратной связи является положительным.

В общем, «G» и «H» являются функциями частоты. Таким образом, обратная связь увеличит чувствительность усиления системы в одном диапазоне частот и уменьшит в другом диапазоне частот. Поэтому мы должны выбирать значения «GH» таким образом, чтобы система была нечувствительной или менее чувствительной к изменениям параметров.

Влияние обратной связи на стабильность

• Система называется стабильной, если ее выход находится под контролем. В противном случае он называется нестабильным.

• В уравнении 2, если значение знаменателя равно нулю (т. Е. GH = -1), выходной сигнал системы управления будет бесконечным. Итак, система управления становится нестабильной.

Система называется стабильной, если ее выход находится под контролем. В противном случае он называется нестабильным.

В уравнении 2, если значение знаменателя равно нулю (т. Е. GH = -1), выходной сигнал системы управления будет бесконечным. Итак, система управления становится нестабильной.

Поэтому мы должны правильно выбрать обратную связь, чтобы сделать систему управления стабильной.

Влияние обратной связи на шум

Чтобы узнать влияние обратной связи на шум, давайте сравним отношения передаточной функции с обратной связью и без нее из-за одного только шумового сигнала.

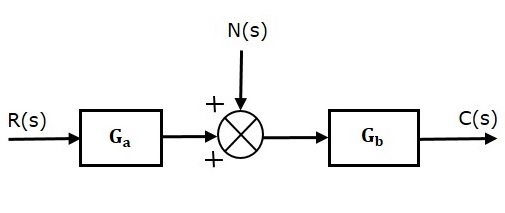
Рассмотрим систему управления без обратной связи с шумовым сигналом, как показано ниже.

Передаточная функция разомкнутого контура из-за одного только шумового сигнала

$\ frac {C (s)} {N (s)} = G_b$ (уравнение 7)

Это получается, делая другой вход $R (s)$ равным нулю.

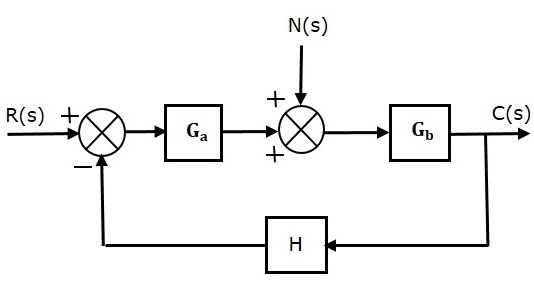
Рассмотрим систему управления с замкнутым контуром с шумовым сигналом, как показано ниже.

Передаточная функция замкнутого контура из-за одного только шумового сигнала

$\ frac {C (s)} {N (s)} = \ frac {G_b} {1 + G_aG_bH}$ (уравнение 8)

Это получается, делая другой вход $R (s)$ равным нулю.

Сравните уравнение 7 и уравнение 8,

В системе управления с обратной связью усиление, вызванное шумовым сигналом, уменьшается на коэффициент $(1 + G_a G_b H)$ при условии, что член $(1 + G_a G_b H)$ больше единицы.

Системы управления — математические модели

Системы управления могут быть представлены с помощью ряда математических уравнений, известных как математическая модель . Эти модели полезны для анализа и проектирования систем управления. Анализ системы управления означает поиск выхода, когда мы знаем вход и математическую модель. Проектирование системы управления означает поиск математической модели, когда мы знаем вход и выход.

В основном используются следующие математические модели.

• Модель дифференциального уравнения
• Модель передаточной функции
• Государственная космическая модель

Давайте обсудим первые две модели в этой главе.

Модель дифференциального уравнения

Модель дифференциальных уравнений представляет собой математическую модель систем управления во временной области. Выполните следующие шаги для модели дифференциального уравнения.

• Применять основные законы к данной системе управления.

• Получите дифференциальное уравнение с точки зрения ввода и вывода, исключив промежуточную переменную (и).

Применять основные законы к данной системе управления.

Получите дифференциальное уравнение с точки зрения ввода и вывода, исключив промежуточную переменную (и).

пример

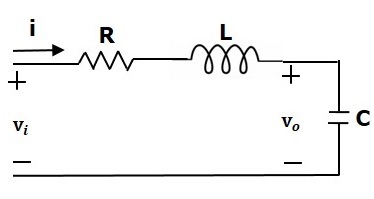
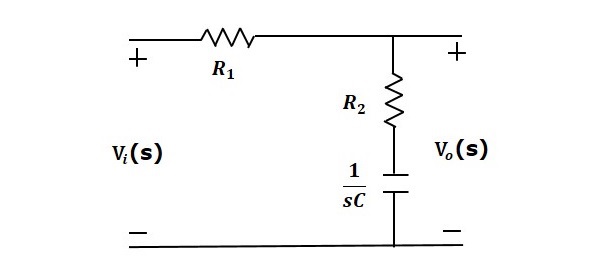
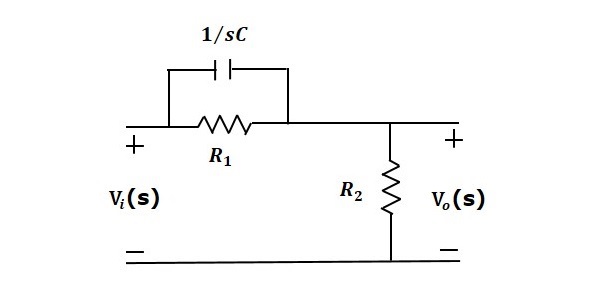
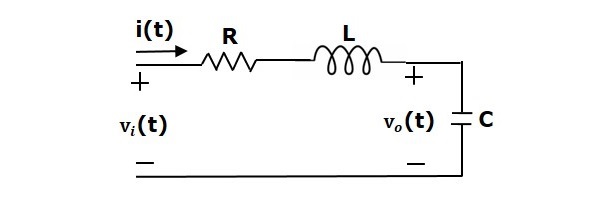
Рассмотрим следующую электрическую систему, как показано на следующем рисунке. Эта схема состоит из резистора, катушки индуктивности и конденсатора. Все эти электрические элементы соединены последовательно . Входное напряжение, приложенное к этой схеме, составляет $v_i$, а напряжение на конденсаторе — это выходное напряжение $v_o$.

Сетчатое уравнение для этой схемы

$$v_i = Ri + L \ гидроразрыва {\ текст {d} я} {\ текст {d} т} + v_o$$

Подставим ток, проходящий через конденсатор $i = c \ frac {\ text {d} v_o} {\ text {d} t}$ в приведенном выше уравнении.

 Rightarrowvi=RC гидроразрыва текстdvo текстdт+LC гидроразрыва текстd2vo текстdт2+vo $$\ Rightarrow \: v_i = RC \ гидроразрыва {\ текст {d} v_o} {\ текст {d} т} + LC \ гидроразрыва {\ текст {d} ^ 2v_o} {\ текст {d} т ^ 2} + v_o$$

$$\ Rightarrow \ frac {\ text {d} ^ 2v_o} {\ text {d} t ^ 2} + \ left (\ frac {R} {L} \ right) \ frac {\ text {d} v_o} {\ text {d} t} + \ left (\ frac {1} {LC} \ right) v_o = \ left (\ frac {1} {LC} \ right) v_i$$

Вышеупомянутое уравнение является дифференциальным уравнением второго порядка.

Модель передаточной функции

Модель передаточной функции — это математическая модель систем управления в s-области. Передаточная функция системы с линейным инвариантом времени (LTI) определяется как отношение преобразования Лапласа на выходе и преобразования Лапласа на входе при условии, что все начальные условия равны нулю.

Если $x (t)$ и $y (t)$ являются входом и выходом системы LTI, то соответствующие преобразования Лапласа равны $X (s)$ и $Y (s)$.

Следовательно, передаточная функция системы LTI равна отношению $Y (s)$ и $X (s)$.

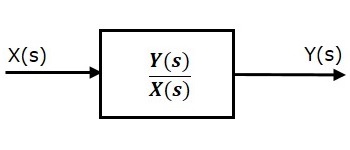
ie,TransferFunction= fracY(s)X(s) $$ie, \: Transfer \: Function = \ frac {Y (s)} {X (s)}$$

Модель передаточной функции системы LTI показана на следующем рисунке.

Здесь мы представили систему LTI с блоком, имеющим передаточную функцию внутри нее. И этот блок имеет вход $X (s)$ и вывод $Y (s)$.

пример

Ранее мы получили дифференциальное уравнение электрической системы в виде

$$\ frac {\ text {d} ^ 2v_o} {\ text {d} t ^ 2} + \ left (\ frac {R} {L} \ right) \ frac {\ text {d} v_o} {\ текст {d} t} + \ left (\ frac {1} {LC} \ right) v_o = \ left (\ frac {1} {LC} \ right) v_i$$

Примените преобразование Лапласа с обеих сторон.

$$s ^ 2V_o (s) + \ left (\ frac {sR} {L} \ right) V_o (s) + \ left (\ frac {1} {LC} \ right) V_o (s) = \ left ( \ frac {1} {LC} \ right) V_i (s)$$

$$\ Rightarrow \ left \ {s ^ 2 + \ left (\ frac {R} {L} \ right) s + \ frac {1} {LC} \ right \} V_o (s) = \ left (\ frac { 1} {LC} \ right) V_i (s)$$

$$\ Rightarrow \ frac {V_o (s)} {V_i (s)} = \ frac {\ frac {1} {LC}} {s ^ 2 + \ left (\ frac {R} {L} \ right) s + \ гидроразрыва {1} {LC}}$$

Куда,

• $v_i (s)$ — преобразование Лапласа входного напряжения $v_i$

• $v_o (s)$ — преобразование Лапласа выходного напряжения $v_o$

$v_i (s)$ — преобразование Лапласа входного напряжения $v_i$

$v_o (s)$ — преобразование Лапласа выходного напряжения $v_o$

Вышеупомянутое уравнение является передаточной функцией электрической системы второго порядка. Модель передаточной функции этой системы показана ниже.

Здесь мы показываем электрическую систему второго порядка с блоком, имеющим передаточную функцию внутри него. И этот блок имеет вход $V_i (s)$ и выход $V_o (s)$.

Моделирование механических систем

В этой главе мы обсудим моделирование дифференциальных уравнений механических систем. Существует два типа механических систем, основанных на типе движения.

• Трансляционные механические системы
• Ротационные механические системы

Моделирование трансляционных механических систем

Поступательные механические системы движутся по прямой . Эти системы в основном состоят из трех основных элементов. Это масса, пружина и приборная панель или демпфер.

Если сила прикладывается к поступательной механической системе, то ей противостоят противоположные силы из-за массы, упругости и трения системы. Поскольку приложенная сила и противоположные силы находятся в противоположных направлениях, алгебраическая сумма сил, действующих на систему, равна нулю. Давайте теперь посмотрим на силу, которой противостоят эти три элемента в отдельности.

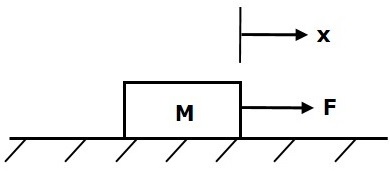
масса

Масса — это свойство тела, которое хранит кинетическую энергию . Если сила применяется к телу, имеющему массу М , то ей противостоит сила противодействия, обусловленная массой. Эта противодействующая сила пропорциональна ускорению тела. Предположим, что эластичность и трение незначительны.

Fm proptoa $$F_m \ propto \: a$$

$$\ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2}$$

$$F = f_m = М \ {\ гидроразрыва текст {D} ^ 2x} {\ текст {d} т ^ 2}$$

Куда,

• F — приложенная сила

• F _m — противодействующая сила, обусловленная массой

• М это масса

• а ускорение

• х смещение

F — приложенная сила

F _m — противодействующая сила, обусловленная массой

М это масса

а ускорение

х смещение

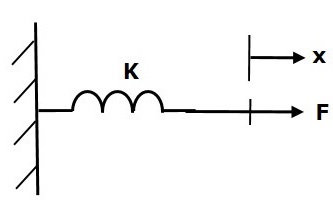
весна

Весна — это элемент, который накапливает потенциальную энергию . Если сила приложена к пружине K , то ей противостоит сила противодействия из-за упругости пружины. Эта противодействующая сила пропорциональна смещению пружины. Предположим, что масса и трение незначительны.

F proptox $$F \ propto \: x$$

$$\ Rightarrow F_k = Kx$$

$$F = F_k = Kx$$

Куда,

• F — приложенная сила

• F _k — противодействующая сила из-за упругости пружины

• К — пружинная постоянная

• х смещение

F — приложенная сила

F _k — противодействующая сила из-за упругости пружины

К — пружинная постоянная

х смещение

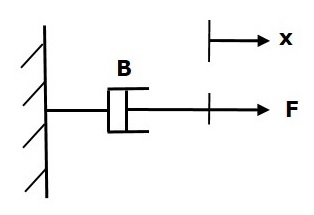
демпфер

Если сила приложена к передней панели B , то ей противостоит противоположная сила из-за трения передней панели. Эта противодействующая сила пропорциональна скорости тела. Предположим, что масса и эластичность незначительны.

Fb propto nu $$F_b \ propto \: \ nu$$

$$\ Rightarrow F_b = B \ nu = B \ frac {\ text {d} x} {\ text {d} t}$$

$$F = F_b = В \ гидроразрыва {\ текст {d} {х} \ текст {D} т}$$

Куда,

• F _b — противодействующая сила из-за трения приборной панели

• B — коэффициент трения

• v скорость

• х смещение

F _b — противодействующая сила из-за трения приборной панели

B — коэффициент трения

v скорость

х смещение

Моделирование вращательных механических систем

Вращательные механические системы движутся вокруг неподвижной оси. Эти системы в основном состоят из трех основных элементов. Это момент инерции, пружина кручения и приборная панель .

Если крутящий момент приложен к вращательной механической системе, то ему противостоят противоположные крутящие моменты из-за момента инерции, упругости и трения системы. Поскольку приложенный крутящий момент и противоположные крутящие моменты находятся в противоположных направлениях, алгебраическая сумма крутящих моментов, действующих на систему, равна нулю. Давайте теперь посмотрим крутящий момент, противостоящий этим трем элементам в отдельности.

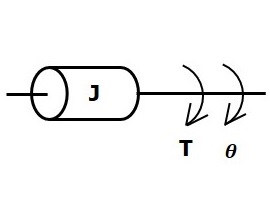
Момент инерции

В поступательной механической системе масса накапливает кинетическую энергию. Аналогично, во вращательной механической системе момент инерции накапливает кинетическую энергию .

Если крутящий момент прикладывается к телу, имеющему момент инерции J , то ему противостоит противоположный крутящий момент, обусловленный моментом инерции. Этот противоположный крутящий момент пропорционален угловому ускорению тела. Предположим, что эластичность и трение незначительны.

Tj propto alpha $$T_j \ propto \: \ alpha$$

$$\ Rightarrow T_j = J \ alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2}$$

$$Т = T_j = J \ гидроразрыва {\ текст {d} ^ 2 \ тета} {\ текст {d} т ^ 2}$$

Куда,

• T — приложенный крутящий момент

• T _j — противодействующий момент из-за момента инерции

• J — момент инерции

• α — угловое ускорение

• θ — угловое смещение

T — приложенный крутящий момент

T _j — противодействующий момент из-за момента инерции

J — момент инерции

α — угловое ускорение

θ — угловое смещение

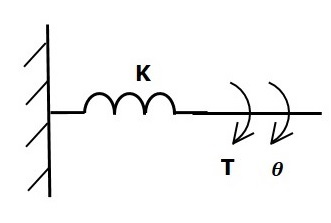
Пружина кручения

В поступательной механической системе пружина накапливает потенциальную энергию. Аналогично, во вращательной механической системе торсионная пружина накапливает потенциальную энергию .

Если крутящий момент приложен к крутильной пружине K , то ему противостоит противоположный крутящий момент из-за упругости крутильной пружины. Этот противоположный крутящий момент пропорционален угловому смещению пружины кручения. Предположим, что момент инерции и трения ничтожен.

Tk propto theta $$T_k \ propto \: \ theta$$

$$\ Rightarrow T_k = K \ theta$$

$$T = T_k = K \ Theta$$

Куда,

• T — приложенный крутящий момент

• T _k — противодействующий момент из-за упругости пружины кручения

• K — постоянная пружины кручения

• θ — угловое смещение

T — приложенный крутящий момент

T _k — противодействующий момент из-за упругости пружины кручения

K — постоянная пружины кручения

θ — угловое смещение

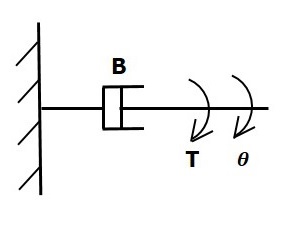
демпфер

Если крутящий момент приложен к передней панели B , то ему противостоит противоположный крутящий момент из-за вращательного трения передней панели. Этот противоположный крутящий момент пропорционален угловой скорости тела. Предположим, что момент инерции и упругости незначительны.

Tb propto omega $$T_b \ propto \: \ omega$$

$$\ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t}$$

$$Т = T_B = В \ гидроразрыва {\ текст {d} \ тета} {\ текст {d} т}$$

Куда,

• T _b — противодействующий крутящий момент из-за вращательного трения передней панели

• B — коэффициент вращательного трения

• ω — угловая скорость

• θ — угловое смещение

T _b — противодействующий крутящий момент из-за вращательного трения передней панели

B — коэффициент вращательного трения

ω — угловая скорость

θ — угловое смещение

Электрические аналогии механических систем

Говорят, что две системы аналогичны друг другу, если выполняются следующие два условия.

• Две системы физически различны
• Дифференциальные уравнения моделирования этих двух систем одинаковы

Электрические системы и механические системы — две физически разные системы. Существует два типа электрических аналогий трансляционных механических систем. Это аналогия силового напряжения и аналога силового тока.

Напряжение аналогии

В аналогии силового напряжения математические уравнения поступательной механической системы сравниваются с сеточными уравнениями электрической системы.

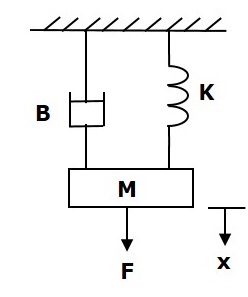
Рассмотрим следующую поступательную механическую систему, как показано на следующем рисунке.

Уравнение силы для этой системы

$$F = f_m + F_b + F_k$$

$\ Rightarrow F = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} + B \ frac {\ text {d} x} {\ text {d} t} + Kx$ (Уравнение 1)

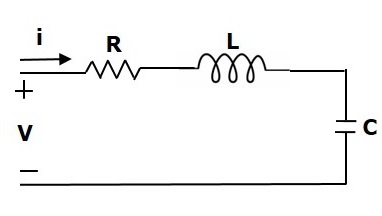
Рассмотрим следующую электрическую систему, как показано на следующем рисунке. Эта схема состоит из резистора, катушки индуктивности и конденсатора. Все эти электрические элементы соединены последовательно. Входное напряжение, приложенное к этой цепи, составляет $V$ вольт, а ток, протекающий по цепи, составляет $i$ Ампер.

Сетчатое уравнение для этой схемы

$V = Ri + L \ frac {\ text {d} i} {\ text {d} t} + \ frac {1} {c} \ int idt$ (уравнение 2)

Замените $i = \ frac {\ text {d} q} {\ text {d} t}$ в уравнении 2.

$$V = R \ гидроразрыва {\ текст {d} д} {\ текст {d} т} + L \ гидроразрыва {\ текст {d} ^ 2q} {\ текст {d} т ^ 2} + \ гидроразрыва { д} {C},$$

$\ Rightarrow V = L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + R \ frac {\ text {d} q} {\ text {d} t} + \ left (\ frac {1} {c} \ right) q$ (уравнение 3)

Сравнивая Уравнение 1 и Уравнение 3, мы получим аналогичные величины поступательной механической системы и электрической системы. Следующая таблица показывает эти аналогичные величины.

Трансляционная Механическая Система	Электрическая система
Сила (F)	Напряжение (V)
Масс-спектр (М)	Индуктивность (L),
Коэффициент трения (B)	Сопротивление (R)
Постоянная весны (K)	Взаимное значение емкости $(\ frac {1} {c})$
Объем (х)	Заряд (д)
Скорость (v)	Ток (я)

Аналогично, существует аналогия напряжения крутящего момента для вращательных механических систем. Давайте теперь поговорим об этой аналогии.

Аналогия по крутящему напряжению

По этой аналогии математические уравнения механической системы вращения сравниваются с сеточными уравнениями электрической системы.

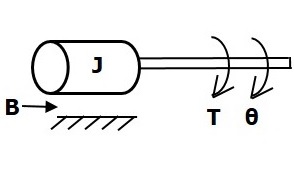
Механизм вращения показан на следующем рисунке.

Уравнение крутящего момента

$$Т = T_j + T_B + T_k$$

$\ Rightarrow T = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} + B \ frac {\ text {d} \ theta} {\ text {d} t} + k \ theta$ (Уравнение 4)

Сравнивая Уравнение 4 и Уравнение 3, мы получим аналогичные величины вращательной механической системы и электрической системы. Следующая таблица показывает эти аналогичные величины.

Ротационная Механическая Система	Электрическая система
Крутящий момент (Т)	Напряжение (V)
Момент инерции (J)	Индуктивность (L),
Коэффициент вращательного трения (B)	Сопротивление (R)
Пружина кручения постоянная (К)	Взаимное значение емкости $(\ frac {1} {c})$
Угловое смещение (θ)	Заряд (д)
Угловая скорость (ω)	Ток (я)

Аналогия силы тока

В аналогии силового тока математические уравнения поступательной механической системы сравниваются с узловыми уравнениями электрической системы.

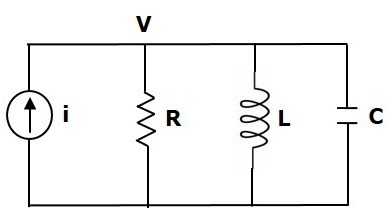
Рассмотрим следующую электрическую систему, как показано на следующем рисунке. Эта схема состоит из источника тока, резистора, катушки индуктивности и конденсатора. Все эти электрические элементы соединены параллельно.

Узловое уравнение

$i = \ frac {V} {R} + \ frac {1} {L} \ int Vdt + C \ frac {\ text {d} V} {\ text {d} t}$ (уравнение 5)

Замените $V = \ frac {\ text {d} \ Psi} {\ text {d} t}$ в уравнении 5.

$$i = \ frac {1} {R} \ frac {\ text {d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi + C \ гидроразрыва {\ текст {d} ^ 2 \ Psi} {\ текст {d} т ^ 2}$$

$\ Rightarrow i = C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} + \ left (\ frac {1} {R} \ right) \ frac {\ text { d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi$ (уравнение 6)

Сравнивая Уравнение 1 и Уравнение 6, мы получим аналогичные величины поступательной механической системы и электрической системы. Следующая таблица показывает эти аналогичные величины.

Трансляционная Механическая Система	Электрическая система
Сила (F)	Ток (я)
Масс-спектр (М)	Емкость (С)
Коэффициент трения (Б)	Взаимное сопротивление $(\ frac {1} {R})$
Пружинная постоянная (К)	Взаимная индуктивность $(\ frac {1} {L})$
Объем (х)	Магнитный поток (ψ)
Скорость (v)	Напряжение (V)

Аналогичным образом, существует аналогия крутящего момента для вращательных механических систем. Давайте теперь обсудим эту аналогию.

Аналогия по крутящему току

По этой аналогии математические уравнения механики вращения сравниваются с уравнениями узловой сетки электрической системы.

Сравнивая Уравнение 4 и Уравнение 6, мы получим аналогичные величины вращательной механической системы и электрической системы. Следующая таблица показывает эти аналогичные величины.

Ротационная Механическая Система	Электрическая система
Крутящий момент (Т)	Ток (я)
Момент инерции (Дж)	Емкость (С)
Коэффициент вращательного трения (B)	Взаимное сопротивление $(\ frac {1} {R})$
Пружина кручения постоянная (К)	Взаимная индуктивность $(\ frac {1} {L})$
Угловое смещение (θ)	Магнитный поток (ψ)
Угловая скорость (ω)	Напряжение (V)

В этой главе мы обсудили электрические аналогии механических систем. Эти аналогии полезны для изучения и анализа неэлектрической системы, такой как механическая система из аналогичной электрической системы.

Системы управления — Блок-схемы

Блок-схемы состоят из одного блока или комбинации блоков. Они используются для представления систем управления в графической форме.

Основные элементы блок-схемы

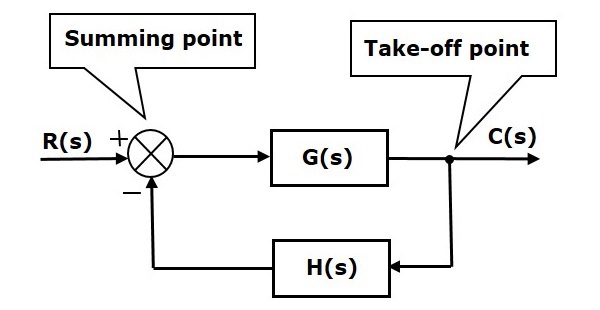
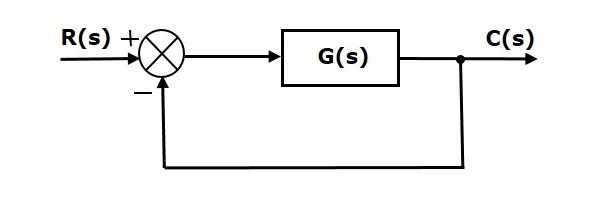
Основными элементами блок-схемы являются блок, точка суммирования и точка взлета. Давайте рассмотрим блок-схему замкнутой системы управления, как показано на следующем рисунке, чтобы идентифицировать эти элементы.

Вышеприведенная блок-схема состоит из двух блоков, имеющих передаточные функции G (s) и H (s). Он также имеет одну точку суммирования и одну точку взлета. Стрелки указывают направление потока сигналов. Давайте теперь обсудим эти элементы один за другим.

блок

Передаточная функция компонента представлена ​​блоком. Блок имеет один вход и один выход.

На следующем рисунке показан блок, имеющий вход X (s), выход Y (s) и передаточную функцию G (s).

Передаточная функция, $G (s) = \ frac {Y (s)} {X (s)}$

$$\ Rightarrow Y (s) = G (s) X (s)$$

Выход блока получается умножением передаточной функции блока на вход.

Суммирующая точка

Суммирующая точка представлена ​​кружком с крестиком (X) внутри. Он имеет два или более входа и один выход. Это производит алгебраическую сумму входных данных. Он также выполняет суммирование или вычитание или комбинацию суммирования и вычитания входов на основе полярности входов. Давайте посмотрим на эти три операции одну за другой.

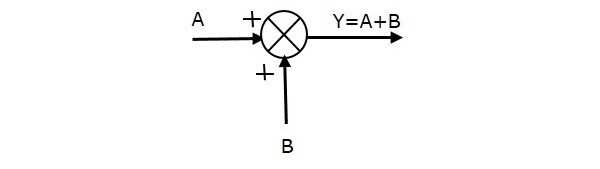
На следующем рисунке показана точка суммирования с двумя входами (A, B) и одним выходом (Y). Здесь входы A и B имеют положительный знак. Таким образом, точка суммирования производит вывод, Y как сумму A и B.

то есть Y = A + B.

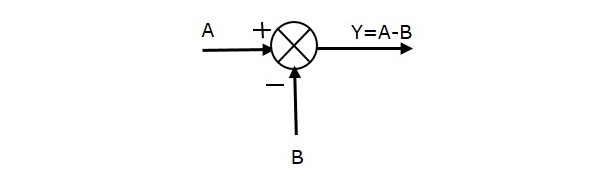
На следующем рисунке показана точка суммирования с двумя входами (A, B) и одним выходом (Y). Здесь входы A и B имеют противоположные знаки, то есть A имеет положительный знак, а B имеет отрицательный знак. Таким образом, точка суммирования выдает выходной Y как разность A и B.

Y = A + (-B) = A — B.

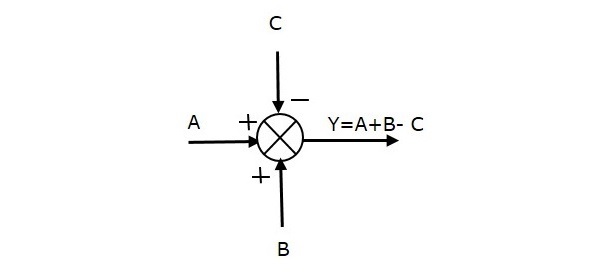
На следующем рисунке показана точка суммирования с тремя входами (A, B, C) и одним выходом (Y). Здесь входы A и B имеют положительные знаки, а C имеет отрицательный знак. Таким образом, точка суммирования выдает результат Y как

Y = A + B + (-C) = A + B — C.

Точка взлета

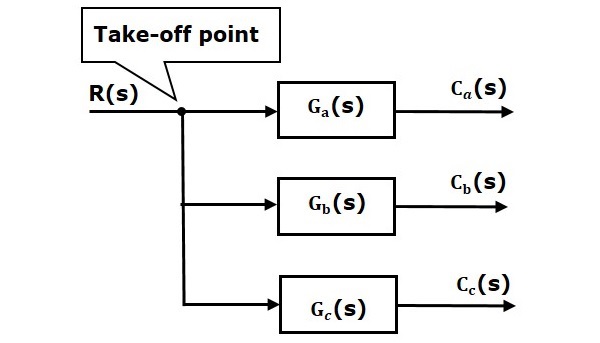
Точка взлета — это точка, из которой один и тот же входной сигнал может проходить через несколько ветвей. Это означает, что с помощью точки взлета мы можем применить один и тот же вход к одному или нескольким блокам, суммируя точки.

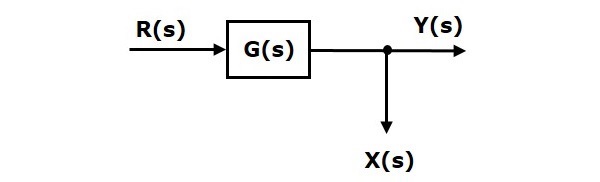
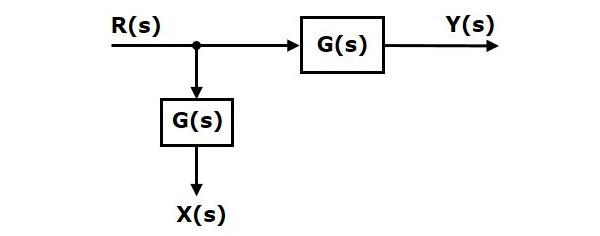
На следующем рисунке точка взлета используется для подключения того же входа R (s) к двум другим блокам.

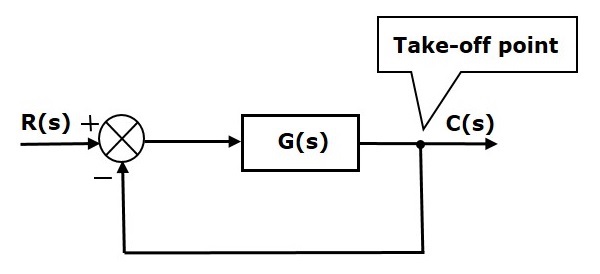
На следующем рисунке точка взлета используется для подключения выхода C (s) в качестве одного из входов к точке суммирования.

Блок-схема представления электрических систем

В этом разделе давайте представим электрическую систему с блок-схемой. Электрические системы содержат в основном три основных элемента — резистор, индуктор и конденсатор .

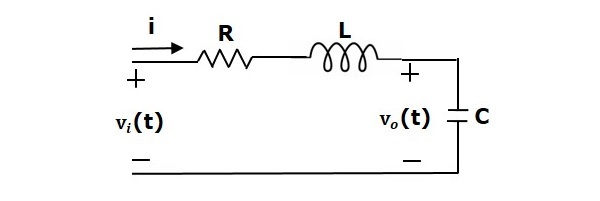
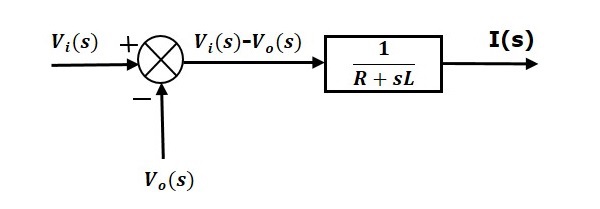
Рассмотрим серию цепей RLC, как показано на следующем рисунке. Где V _i (t) и V _o (t) — входные и выходные напряжения. Пусть i (t) будет током, проходящим через цепь. Эта схема находится во временной области.

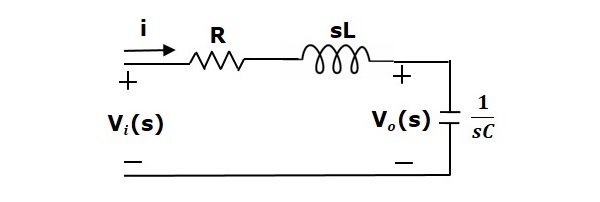
Применяя преобразование Лапласа к этой схеме, получим схему в s-области. Схема такая, как показано на следующем рисунке.

Из приведенной выше схемы мы можем написать

$$I (S) = \ гидроразрыва {V_i (ы) -V_o (ы)} {R + Sl}$$

$\ Rightarrow I (s) = \ left \ {\ frac {1} {R + sL} \ right \} \ left \ {V_i (s) -V_o (s) \ right \}$ (уравнение 1)

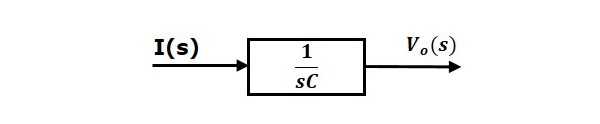
$V_o (s) = \ left (\ frac {1} {sC} \ right) I (s)$ (уравнение 2)

Давайте теперь нарисуем блок-схемы для этих двух уравнений в отдельности. И затем объедините эти блок-схемы правильно, чтобы получить общую блок-схему серии RLC Circuit (s-domain).

Уравнение 1 может быть реализовано с помощью блока, имеющего передаточную функцию $\ frac {1} {R + sL}$. Вход и выход этого блока: $\ left \ {V_i (s) -V_o (s) \ right \}$ и $I (s)$. Нам требуется точка суммирования, чтобы получить $\ left \ {V_i (s) -V_o (s) \ right \}$. Блок-схема уравнения 1 показана на следующем рисунке.

Уравнение 2 может быть реализовано с помощью блока, имеющего передаточную функцию $\ frac {1} {sC}$. Вход и выход этого блока — $I (s)$ и $V_o (s)$. Блок-схема уравнения 2 показана на следующем рисунке.

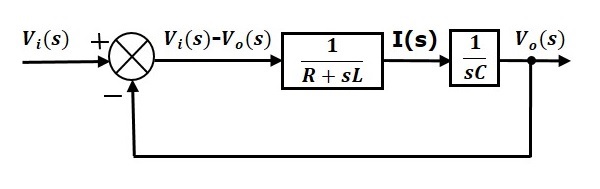
Общая блок-схема серии RLC Circuit (s-domain) показана на следующем рисунке.

Точно так же вы можете нарисовать структурную схему любой электрической цепи или системы, просто следуя этой простой процедуре.

• Преобразуйте электрическую цепь временной области в электрическую цепь s-области, применяя преобразование Лапласа.

• Запишите уравнения для тока, проходящего через все элементы последовательных ветвей, и напряжения на всех ветвях шунта.

• Нарисуйте блок-схемы для всех вышеперечисленных уравнений в отдельности.

• Правильно объедините все эти блок-схемы, чтобы получить общую блок-схему электрической цепи (s-домен).

Преобразуйте электрическую цепь временной области в электрическую цепь s-области, применяя преобразование Лапласа.

Запишите уравнения для тока, проходящего через все элементы последовательных ветвей, и напряжения на всех ветвях шунта.

Нарисуйте блок-схемы для всех вышеперечисленных уравнений в отдельности.

Правильно объедините все эти блок-схемы, чтобы получить общую блок-схему электрической цепи (s-домен).

Системы управления — блок-схема алгебры

Алгебра блок-схем — это не что иное, как алгебра, связанная с основными элементами блок-диаграммы. Эта алгебра имеет дело с графическим представлением алгебраических уравнений.

Основные соединения для блоков

Существует три основных типа соединений между двумя блоками.

Последовательное соединение

Последовательное соединение также называется каскадным соединением . На следующем рисунке два блока, имеющие передаточные функции $G_1 (s)$ и $G_2 (s)$, соединены последовательно.

Для этой комбинации мы получим вывод $Y (s)$ как

$$Y (s) = G_2 (ы) Z (S)$$

Где $Z (s) = G_1 (s) X (s)$

$$\ Rightarrow Y (s) = G_2 (s) [G_1 (s) X (s)] = G_1 (s) G_2 (s) X (s)$$

$$\ Rightarrow Y (s) = \ lbrace G_1 (s) G_2 (s) \ rbrace X (s)$$

Сравните это уравнение со стандартной формой выходного уравнения, $Y (s) = G (s) X (s)$. Где $G (s) = G_1 (s) G_2 (s)$.

Это означает, что мы можем представить последовательное соединение двух блоков одним блоком. Передаточная функция этого единственного блока является произведением передаточных функций этих двух блоков. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить последовательное соединение n блоков с одним блоком. Передаточная функция этого единственного блока является произведением передаточных функций всех этих «n» блоков.

Параллельное соединение

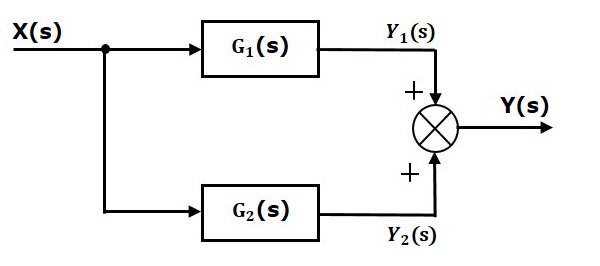
Блоки, которые соединены параллельно, будут иметь одинаковый вход . На следующем рисунке два блока, имеющие передаточные функции $G_1 (s)$ и $G_2 (s)$, соединены параллельно. Выходы этих двух блоков подключены к точке суммирования.

Для этой комбинации мы получим вывод $Y (s)$ как

$$Y (s) = Y_1 (тв) + Y_2 (ы)$$

Где $Y_1 (s) = G_1 (s) X (s)$ и $Y_2 (s) = G_2 (s) X (s)$

$$\ Rightarrow Y (s) = G_1 (s) X (s) + G_2 (s) X (s) = \ lbrace G_1 (s) + G_2 (s) \ rbrace X (s)$$

Сравните это уравнение со стандартной формой выходного уравнения, $Y (s) = G (s) X (s)$.

Где $G (s) = G_1 (s) + G_2 (s)$.

Это означает, что мы можем представить параллельное соединение двух блоков с одним блоком. Передаточная функция этого единственного блока является суммой передаточных функций этих двух блоков. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить параллельное соединение n блоков с одним блоком. Передаточная функция этого единственного блока является алгебраической суммой передаточных функций всех этих «n» блоков.

Обратная связь

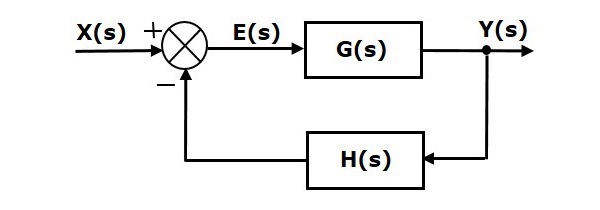
Как мы уже говорили в предыдущих главах, существует два типа обратной связи — положительная и отрицательная. На следующем рисунке показана система контроля отрицательной обратной связи. Здесь два блока с передаточными функциями $G (s)$ и $H (s)$ образуют замкнутый цикл.

Выход точки суммирования —

$$E (S) = X (S) -H (ы) Y (ы)$$

Выход $Y (s)$ —

$$Y (s) = Е (ы) О (ы)$$

Замените значение $E (s)$ в приведенном выше уравнении.

$$Y (s) = \ left \ {X (s) -H (s) Y (s) \ rbrace G (s) \ right \}$$

$$Y (s) \ left \ {1 + G (s) H (s) \ rbrace = X (s) G (s) \ right \}$$

$$\ Rightarrow \ frac {Y (s)} {X (s)} = \ frac {G (s)} {1 + G (s) H (s)}$$

Следовательно, передаточная функция замкнутого контура с отрицательной обратной связью равна $\ frac {G (s)} {1 + G (s) H (s)}$

Это означает, что мы можем представить соединение отрицательной обратной связи двух блоков с одним блоком. Передаточная функция этого одиночного блока является передаточной функцией обратной связи с обратной связью. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить соединение положительного отклика двух блоков с одним блоком. Передаточная функция этого единственного блока является передаточной функцией замкнутого контура положительной обратной связи, т. Е. $\ Frac {G (s)} {1-G (s) H (s)}$

Блок-схема алгебры суммирования баллов

Есть две возможности смещения точек суммирования относительно блоков —

• Смещение точки суммирования после блока
• Смещение точки суммирования перед блоком

Давайте теперь посмотрим, какие меры необходимо предпринять в вышеупомянутых двух случаях один за другим.

Смещение точки суммирования после блока

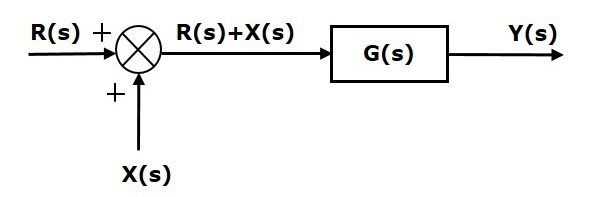
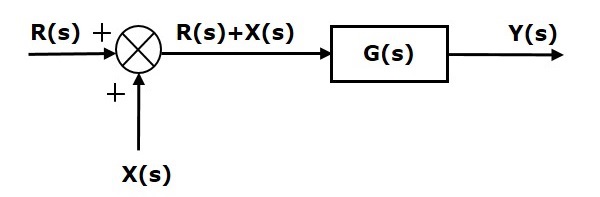
Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка суммирования присутствует перед блоком.

Точка суммирования имеет два входа $R (s)$ и $X (s)$. Выходные данные: $\ left \ {R (s) + X (s) \ right \}$.

Таким образом, вход в блок $G (s)$ равен $\ left \ {R (s) + X (s) \ right \}$, а его выход —

$$Y (s) = G (s) \ left \ {R (s) + X (s) \ right \}$$

$\ Rightarrow Y (s) = G (s) R (s) + G (s) X (s)$ (Уравнение 1)

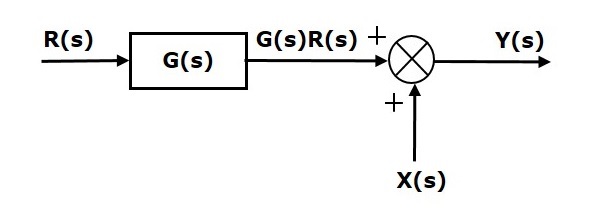
Теперь сдвиньте точку суммирования после блока. Эта блок-схема показана на следующем рисунке.

Выход блока $G (s)$ равен $G (s) R (s)$.

Выход точки суммирования

$Y (s) = G (s) R (s) + X (s)$ (уравнение 2)

Сравните уравнение 1 и уравнение 2.

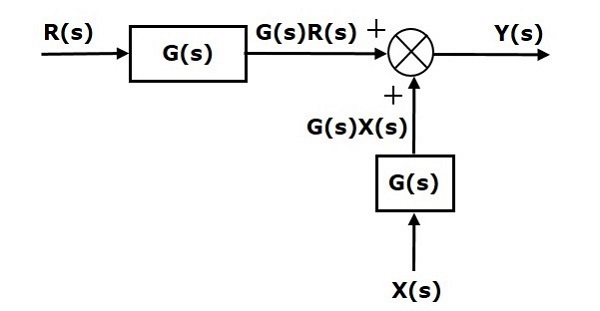
Первое слагаемое ′G(s)R(s)′$'G (s) R (s)'$ одинаково в обоих уравнениях. Но есть разница во втором семестре. Чтобы получить второй член, такой же, нам нужен еще один блок $G (s)$. Он имеет входные данные $X (s)$, а выходные данные этого блока задаются в качестве входных данных для точки суммирования вместо $X (s)$. Эта блок-схема показана на следующем рисунке.

Смещение точки суммирования перед блоком

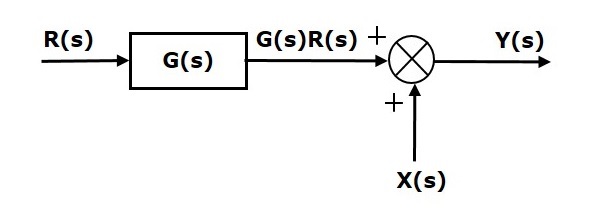
Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка суммирования присутствует после блока.

Выход этой блок-схемы —

$Y (s) = G (s) R (s) + X (s)$ (уравнение 3)

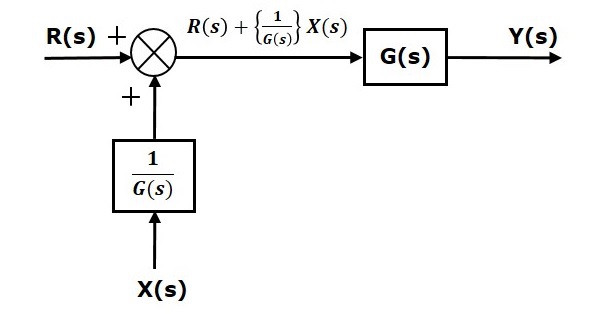
Теперь сдвиньте точку суммирования перед блоком. Эта блок-схема показана на следующем рисунке.

Выход этой блок-схемы —

$Y (S) = G (s) R (s) + G (s) X (s)$ (Уравнение 4)

Сравните уравнение 3 и уравнение 4,

Первое слагаемое ′G(s)R(s)′$'G (s) R (s)'$ одинаково в обоих уравнениях. Но есть разница во втором семестре. Чтобы получить второй член, такой же, нам нужен еще один блок $\ frac {1} {G (s)}$. Он имеет входные данные $X (s)$, а выходные данные этого блока задаются в качестве входных данных для точки суммирования вместо $X (s)$. Эта блок-схема показана на следующем рисунке.

Алгебра блок-схем для точек взлета

Есть две возможности сдвига точек взлета относительно блоков —

• Сдвиг точки взлета после блока
• Сдвиг точки взлета перед блоком

Давайте теперь посмотрим, какие меры должны быть предприняты в вышеупомянутых двух случаях, один за другим.

Сдвиг точки взлета после блока

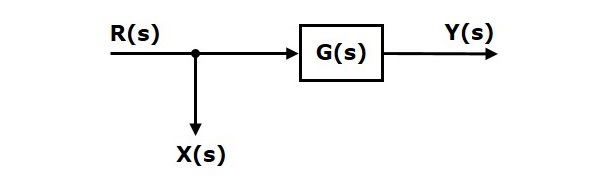
Рассмотрим блок-схему, показанную на следующем рисунке. В этом случае точка взлета присутствует перед блоком.

Здесь $X (s) = R (s)$ и $Y (s) = G (s) R (s)$

Когда вы сдвигаете точку взлета после блока, выходные данные $Y (s)$ будут такими же. Но есть разница в значении $X (s)$. Итак, чтобы получить то же значение $X (s)$, нам потребуется еще один блок $\ frac {1} {G (s)}$. Он имеет вход $Y (s)$, а вывод — $X (s)$. Эта блок-схема показана на следующем рисунке.

Сдвиг точки взлета перед блоком

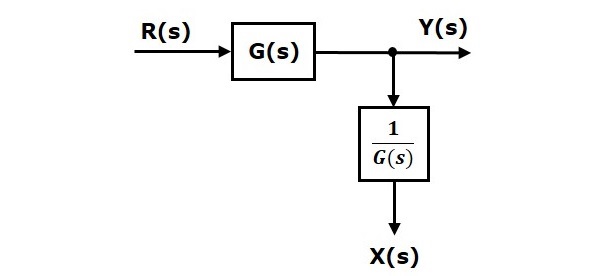
Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка взлета присутствует после блока.

Здесь $X (s) = Y (s) = G (s) R (s)$

Когда вы сдвигаете точку взлета перед блоком, выходные данные $Y (s)$ будут такими же. Но есть разница в значении $X (s)$. Итак, чтобы получить то же значение $X (s)$, нам потребуется еще один блок $G (s)$. Он имеет вход $R (s)$, а вывод — $X (s)$. Эта блок-схема показана на следующем рисунке.

Системы управления — сокращение блок-схемы

Концепции, обсуждаемые в предыдущей главе, полезны для сокращения (упрощения) блок-схем.

Правила сокращения блок-схем

Следуйте этим правилам для упрощения (уменьшения) блок-схемы, которая состоит из множества блоков, точек суммирования и точек взлета.

• Правило 1 — Проверьте блоки, соединенные последовательно и упростите.

• Правило 2 — Проверьте блоки, соединенные параллельно, и упростите.

• Правило 3 — Проверьте блоки, подключенные в петле обратной связи, и упростите.

• Правило 4 — Если есть трудности с точкой взлета при упрощении, сдвиньте ее вправо.

• Правило 5 — Если есть трудности с суммированием точки при упрощении, сдвиньте ее влево.

• Правило 6 — Повторяйте вышеуказанные шаги, пока не получите упрощенную форму, то есть один блок.

Правило 1 — Проверьте блоки, соединенные последовательно и упростите.

Правило 2 — Проверьте блоки, соединенные параллельно, и упростите.

Правило 3 — Проверьте блоки, подключенные в петле обратной связи, и упростите.

Правило 4 — Если есть трудности с точкой взлета при упрощении, сдвиньте ее вправо.

Правило 5 — Если есть трудности с суммированием точки при упрощении, сдвиньте ее влево.

Правило 6 — Повторяйте вышеуказанные шаги, пока не получите упрощенную форму, то есть один блок.

Примечание . Передаточная функция, присутствующая в этом отдельном блоке, является передаточной функцией всей блок-схемы.

пример

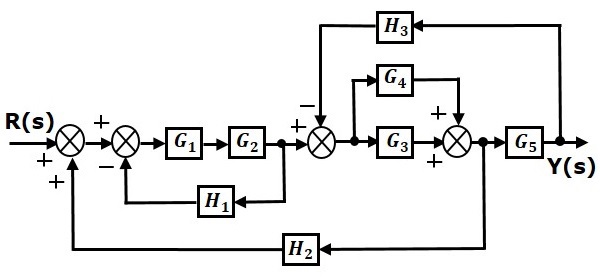
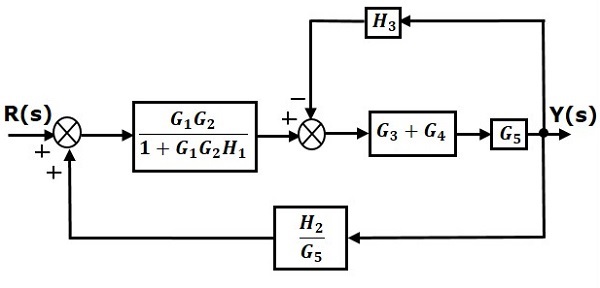
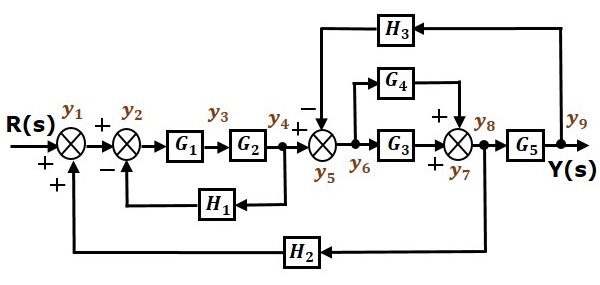
Рассмотрим блок-схему, показанную на следующем рисунке. Давайте упростим (уменьшим) эту блок-схему, используя правила сокращения блок-схем.

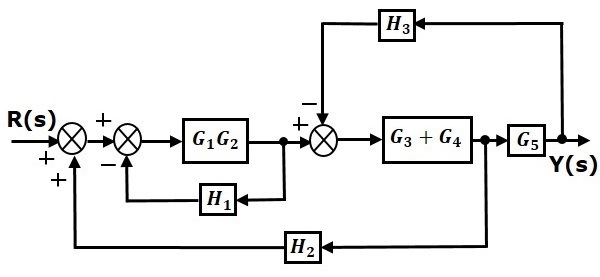
Шаг 1 — Используйте правило 1 для блоков $G_1$ и $G_2$. Используйте правило 2 для блоков $G_3$ и $G_4$. Модифицированная блок-схема показана на следующем рисунке.

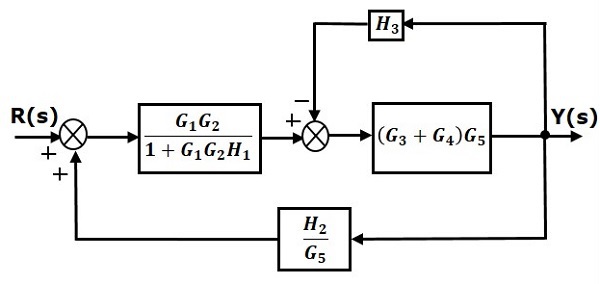
Шаг 2 — Используйте правило 3 для блоков $G_1G_2$ и $H_1$. Используйте Правило 4 для смещения точки взлета после блока $G_5$. Модифицированная блок-схема показана на следующем рисунке.

Шаг 3 — Используйте правило 1 для блоков $(G_3 + G_4)$ и $G_5$. Модифицированная блок-схема показана на следующем рисунке.

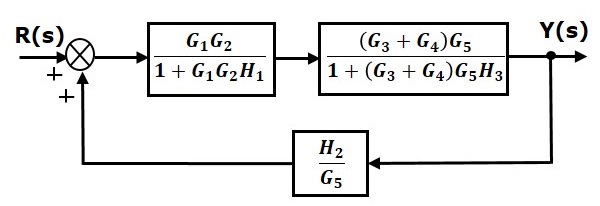
Шаг 4 — Используйте правило 3 для блоков $(G_3 + G_4) G_5$ и $H_3$. Модифицированная блок-схема показана на следующем рисунке.

Шаг 5 — Используйте Правило 1 для блоков, соединенных последовательно. Модифицированная блок-схема показана на следующем рисунке.

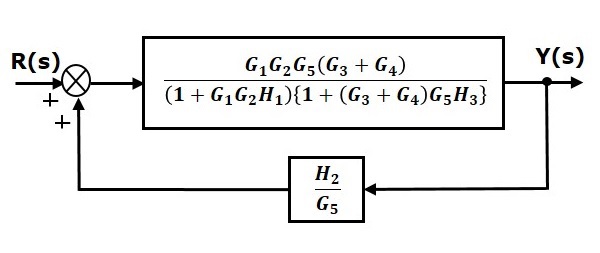
Шаг 6 — Используйте правило 3 для блоков, подключенных в петле обратной связи. Модифицированная блок-схема показана на следующем рисунке. Это упрощенная блок-схема.

Следовательно, передаточная функция системы

$$\ frac {Y (s)} {R (s)} = \ frac {G_1G_2G_5 ^ 2 (G_3 + G_4)} {(1 + G_1G_2H_1) \ lbrace 1+ (G_3 + G_4) G_5H_3 \ rbrace G_5-G_1G_2G_5 (G_3 + G_4) H_2}$$

Примечание. Выполните следующие действия, чтобы рассчитать передаточную функцию блок-схемы, имеющей несколько входов.

• Шаг 1 — Найти передаточную функцию блок-схемы, рассматривая по одному входу за раз, а оставшиеся входы сделать равными нулю.

• Шаг 2 — Повторите шаг 1 для оставшихся входов.

• Шаг 3 — Получить общую функцию передачи, добавив все эти функции передачи.

Шаг 1 — Найти передаточную функцию блок-схемы, рассматривая по одному входу за раз, а оставшиеся входы сделать равными нулю.

Шаг 2 — Повторите шаг 1 для оставшихся входов.

Шаг 3 — Получить общую функцию передачи, добавив все эти функции передачи.

Процесс сокращения структурной схемы занимает больше времени для сложных систем. Потому что мы должны нарисовать (частично упрощенную) блок-схему после каждого шага. Итак, чтобы преодолеть этот недостаток, используйте графики потока сигналов (представление).

В следующих двух главах мы обсудим концепции, связанные с графиками потока сигналов, т. Е. Как представить график потока сигналов из заданной блок-схемы и вычислить передаточную функцию, просто используя формулу усиления без выполнения какого-либо процесса сокращения.

Системы управления — графики потоков сигналов

Граф потока сигналов является графическим представлением алгебраических уравнений. В этой главе давайте обсудим основные понятия, связанные с графиком потоков сигналов, а также научимся рисовать графики потоков сигналов.

Основные элементы графика потока сигналов

Узлы и ветви являются основными элементами графа потока сигналов.

Узел

Узел — это точка, представляющая переменную или сигнал. Существует три типа узлов — узел ввода, узел вывода и смешанный узел.

• Входной узел — это узел, который имеет только исходящие ветви.

• Выходной узел — это узел, который имеет только входящие ветви.

• Смешанный узел — это узел, который имеет как входящие, так и исходящие ветви.

Входной узел — это узел, который имеет только исходящие ветви.

Выходной узел — это узел, который имеет только входящие ветви.

Смешанный узел — это узел, который имеет как входящие, так и исходящие ветви.

пример

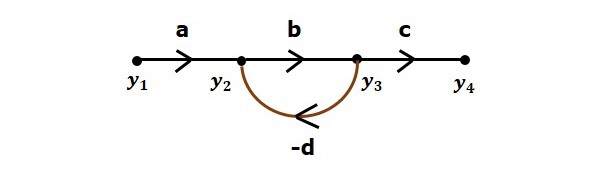
Давайте рассмотрим следующий график потока сигналов для идентификации этих узлов.

• Узлами, представленными в этом графике потока сигналов, являются y ₁ , y ₂ , y ₃ и y ₄ .

• y ₁ и y ₄ — это входной узел и выходной узел соответственно.

• y ₂ и y ₃ — смешанные узлы .

Узлами, представленными в этом графике потока сигналов, являются y ₁ , y ₂ , y ₃ и y ₄ .

y ₁ и y ₄ — это входной узел и выходной узел соответственно.

y ₂ и y ₃ — смешанные узлы .

Ветка

Ветвь — это отрезок, соединяющий два узла. Он имеет как усиление, так и направление . Например, в приведенном выше графике потока сигналов есть четыре ветви. Эти ветви имеют усиление a, b, c и -d .

Построение графика потока сигналов

Построим граф потока сигналов, рассмотрев следующие алгебраические уравнения:

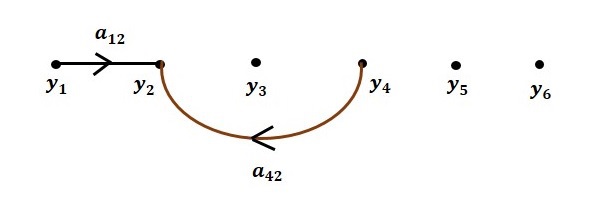
$$y_2 = а_ {12} y_1 + а_ {42} y_4$$

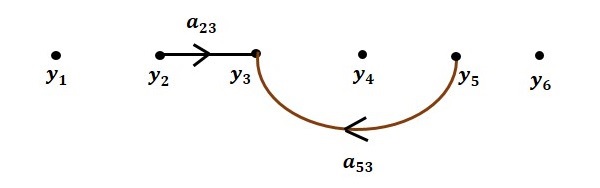
$$y_3 = а_ {23} y_2 + а_ {53} y_5$$

$$y_4 = а_ {34} y_3$$

$$y_5 = а_ {45} y_4 + а_ {35} y_3$$

$$y_6 = а_ {56} y_5$$

В этом графике потока сигналов будет шесть узлов (y ₁ , y ₂ , y ₃ , y ₄ , y ₅ и y ₆ ) и восемь ветвей . Прибыль филиалов составляет ₁₂ , ₂₃ , ₃₄ , ₄₅ , ₅₆ , ₄₂ , ₅₃ и ₃₅ .

Чтобы получить общий график потока сигналов, нарисуйте график потока сигналов для каждого уравнения, затем объедините все эти графики потока сигналов и затем выполните шаги, приведенные ниже —

Шаг 1. Граф потока сигналов для $y_2 = a_ {13} y_1 + a_ {42} y_4$ показан на следующем рисунке.

Шаг 2 — Граф потока сигналов для $y_3 = a_ {23} y_2 + a_ {53} y_5$ показан на следующем рисунке.

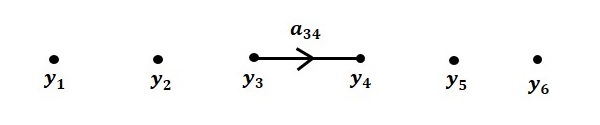
Шаг 3 — График потока сигналов для $y_4 = a_ {34} y_3$ показан на следующем рисунке.

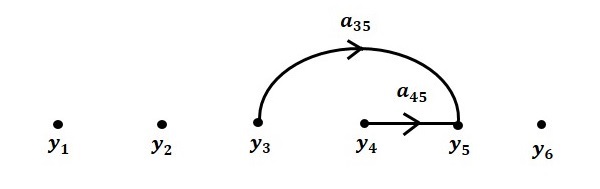
Шаг 4. Граф потока сигналов для $y_5 = a_ {45} y_4 + a_ {35} y_3$ показан на следующем рисунке.

Шаг 5 — График потока сигналов для $y_6 = a_ {56} y_5$ показан на следующем рисунке.

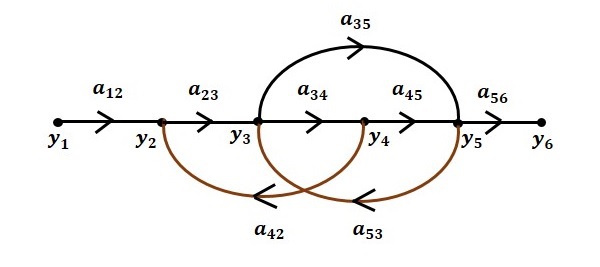
Шаг 6 — График потока сигналов всей системы показан на следующем рисунке.

Преобразование блок-схем в графики потоков сигналов

Выполните следующие шаги для преобразования блок-схемы в ее эквивалентный график потока сигналов.

• Представьте все сигналы, переменные, точки суммирования и точки взлета блок-схемы в виде узлов на графике потока сигналов.

• Представлять блоки блок-схемы в виде ветвей на графике потока сигналов.

• Представлять передаточные функции внутри блоков блок-схемы в виде коэффициентов усиления ветвей на графике потока сигналов.

• Соедините узлы согласно блок-схеме. Если есть связь между двумя узлами (но между ними нет блока), тогда представьте усиление ветви как единое целое. Например , между точками суммирования, между точкой суммирования и точкой взлета, между входом и точкой суммирования, между точкой взлета и выходом.

Представьте все сигналы, переменные, точки суммирования и точки взлета блок-схемы в виде узлов на графике потока сигналов.

Представлять блоки блок-схемы в виде ветвей на графике потока сигналов.

Представлять передаточные функции внутри блоков блок-схемы в виде коэффициентов усиления ветвей на графике потока сигналов.

Соедините узлы согласно блок-схеме. Если есть связь между двумя узлами (но между ними нет блока), тогда представьте усиление ветви как единое целое. Например , между точками суммирования, между точкой суммирования и точкой взлета, между входом и точкой суммирования, между точкой взлета и выходом.

пример

Давайте преобразуем следующую блок-схему в ее эквивалентный граф потока сигналов.

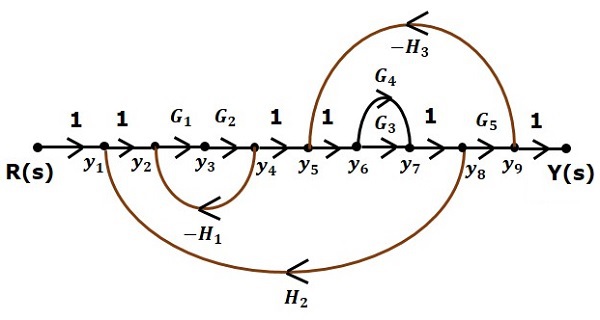
Представьте входной сигнал $R (s)$ и выходной сигнал $C (s)$ блок-схемы как входной узел $R (s)$ и выходной узел $C (s)$ графика потока сигналов.

Просто для справки, остальные узлы (от y ₁ до y ₉ ) помечены на блок-схеме. Есть девять узлов, кроме входных и выходных узлов. Это четыре узла для четырех точек суммирования, четыре узла для четырех точек взлета и один узел для переменной между блоками $G_1$ и $G_2$.

На следующем рисунке показан график эквивалентного потока сигналов.

С помощью формулы усиления Мейсона (обсуждаемой в следующей главе) вы можете рассчитать передаточную функцию этого графика потока сигналов. Это преимущество графиков потока сигналов. Здесь нам не нужно упрощать (уменьшать) графики потока сигналов для расчета передаточной функции.

Mason’s Gain Formula

Давайте теперь обсудим формулу усиления Мэйсона. Предположим, что в графе потока сигналов есть «N» прямых путей. Усиление между входными и выходными узлами графа потока сигналов является ничем иным, как передаточной функцией системы. Его можно рассчитать по формуле усиления Мейсона.

Формула усиления Мэйсона

$$T = \ frac {C (s)} {R (s)} = \ frac {\ Sigma ^ N _ {i = 1} P_i \ Delta _i} {\ Delta}$$

Куда,

• C (s) — выходной узел

• R (s) — входной узел

• T — передаточная функция или усиление между $R (s)$ и $C (s)$.

• P _i — это i- ^й коэффициент усиления прямого пути

C (s) — выходной узел

R (s) — входной узел

T — передаточная функция или усиление между $R (s)$ и $C (s)$.

P _i — это i- ^й коэффициент усиления прямого пути

 Delta=1−(суммаизвсеотдельныйциклвыигрыш)$\ Delta = 1- (сумма \: из \: все \: отдельный \: цикл \: выигрыш)$

$+ (сумма \: of \: gain \: products \: of \: all \: возможно \: two \: nontouching \: loops)$

$$- (сумма \: of \: gain \: products \: of \: all \: возможно \: три \: неприкосновение \: циклы) + ...$$

Δ _i получается из Δ путем удаления петель, которые касаются i- ^го прямого пути .

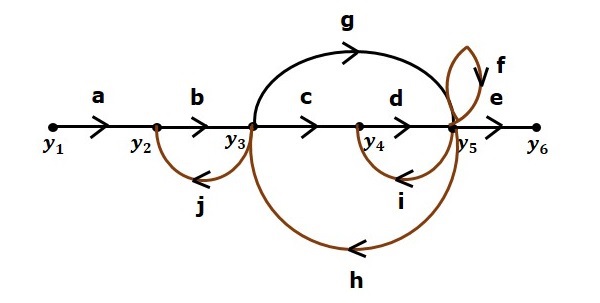
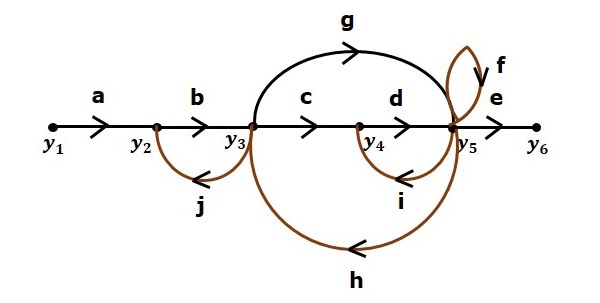
Рассмотрим следующий график потока сигналов, чтобы понять основную терминологию, используемую здесь.

Дорожка

Это обход ветвей от одного узла к любому другому узлу в направлении стрелок ветвления. Он не должен проходить через какой-либо узел более одного раза.

Примеры — $y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5$ и $y_5 \ rightarrow y_3 \ rightarrow y_2$

Прямой путь

Путь, который существует от входного узла до выходного узла, известен как прямой путь .

Примеры — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$ и $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

Прямой путь

Это получается путем вычисления произведения всех ветвей усиления прямого пути.

Примеры — $abcde$ — усиление прямого пути для $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$, а abge — усиление прямого пути $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

петля

Путь, который начинается с одного узла и заканчивается в том же узле, называется циклом . Следовательно, это закрытый путь.

Примеры — $y_2 \ rightarrow y_3 \ rightarrow y_2$ и $y_3 \ rightarrow y_5 \ rightarrow y_3$.

Loop Gain

Это получается путем вычисления произведения всех ветвей усиления цикла.

Примеры — $b_j$ — это усиление цикла для $y_2 \ rightarrow y_3 \ rightarrow y_2$, а $g_h$ — это усиление цикла для $y_3 \ rightarrow y_5 \ rightarrow y_3$.

Бесконтактные петли

Это петли, которые не должны иметь общего узла.

Примеры . Циклы, $y_2 \ rightarrow y_3 \ rightarrow y_2$ и $y_4 \ rightarrow y_5 \ rightarrow y_4$, не затрагиваются.

Расчет передаточной функции по формуле усиления Мэйсона

Рассмотрим тот же график потока сигналов для нахождения передаточной функции.

• Количество прямых путей, N = 2.

• Первый прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$.

• Первое усиление прямого пути, $p_1 = abcde$.

• Второй прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

• Второй прямой путь усиления, $p_2 = abge$.

• Количество отдельных петель, L = 5.

• Циклы — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_3 \ rightarrow y_5 \ rightarrow y_3$, $y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_3$, $y_4 \ rightarrow y_5 \ rightarrow y_4$ и $yar_5$ y_5 $.

• Усиление контура — $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ и $l_5 = f$.

• Количество двух не соприкасающихся петель = 2.

• Первая пара неприкасающих циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_4 \ rightarrow y_5 \ rightarrow y_4$.

• Произведение усиления первой пары неприкосновенных циклов, $l_1l_4 = bjdi$

• Вторая пара неприкосновенных циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_5 \ rightarrow y_5$.

• Произведение усиления второй пары неприкосновенных циклов — $l_1l_5 = bjf$

Количество прямых путей, N = 2.

Первый прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$.

Первое усиление прямого пути, $p_1 = abcde$.

Второй прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

Второй прямой путь усиления, $p_2 = abge$.

Количество отдельных петель, L = 5.

Циклы — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_3 \ rightarrow y_5 \ rightarrow y_3$, $y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_3$, $y_4 \ rightarrow y_5 \ rightarrow y_4$ и $yar_5$ y_5 $.

Усиление контура — $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ и $l_5 = f$.

Количество двух не соприкасающихся петель = 2.

Первая пара неприкасающих циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_4 \ rightarrow y_5 \ rightarrow y_4$.

Произведение усиления первой пары неприкосновенных циклов, $l_1l_4 = bjdi$

Вторая пара неприкосновенных циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_5 \ rightarrow y_5$.

Произведение усиления второй пары неприкосновенных циклов — $l_1l_5 = bjf$

Большее количество (более двух) не соприкасающихся петель не присутствует в этом графике потока сигналов.

Мы знаем,

$\ Delta = 1- (сумма \: из \: все \: отдельный \: цикл \: выигрыш)$

$+ (сумма \: of \: gain \: products \: of \: all \: возможно \: two \: nontouching \: loops)$

$$- (сумма \: of \: gain \: products \: of \: all \: возможно \: три \: неприкосновение \: циклы) + ...$$

Подставим значения в приведенное выше уравнение,

$\ Delta = 1- (bj + gh + cdh + di + f) + (bjdi + bjf) - (0)$

$\ Rightarrow \ Delta = 1- (BJ + GH + CDH + D + F) + BJDI + BJF$

Нет петли, которая не касается первого прямого пути.

Итак, $\ Delta_1 = 1$.

Аналогично, $\ Delta_2 = 1$. Так как нет петли, которая не касается второго прямого пути.

Заменить, N = 2 в формуле усиления Мейсона

$$T = \ frac {C (s)} {R (s)} = \ frac {\ Sigma ^ 2 _ {i = 1} P_i \ Delta _i} {\ Delta}$$

$$Т = \ гидроразрыва {C (S)} {R (S)} = \ {гидроразрыва P_1 \ Delta_1 + P_2 \ Delta_2} {\ Delta}$$

Подставьте все необходимые значения в приведенное выше уравнение.

$$Т = \ гидроразрыва {C (S)} {R (S)} = \ {гидроразрыва (ABCDE) 1+ (abge) 1} {1- (Ь + GH + CDH + ди + ж) + bjdi + BJF }$$

$$\ Rightarrow T = \ frac {C (s)} {R (s)} = \ frac {(abcde) + (abge)} {1- (bj + gh + cdh + di + f) + bjdi + bjf }$$

Следовательно, передаточная функция —

$$ Т = \ гидроразрыва {C (S)} {R (S)} = \ {гидроразрыва (ABCDE) + (abge)} {1- (Ь + GH + CDH + ди + ж) + bjdi + BJF} $ $

Системы управления — анализ времени отклика

Мы можем проанализировать реакцию систем управления как во временной, так и в частотной областях. Мы обсудим анализ частотных характеристик систем управления в следующих главах. Давайте теперь обсудим анализ времени отклика систем управления.

Что такое время отклика?

Если выходной сигнал системы управления для входа изменяется во времени, то он называется временной реакцией системы управления. Время отклика состоит из двух частей.

• Переходный ответ
• Устойчивый государственный ответ

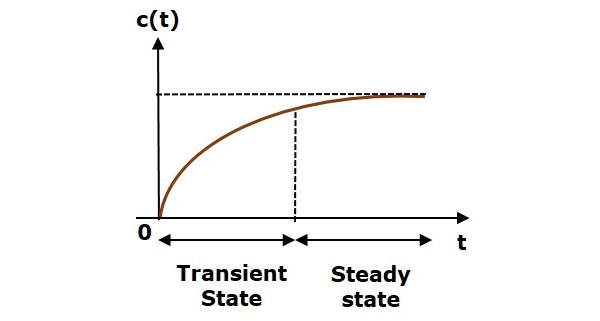
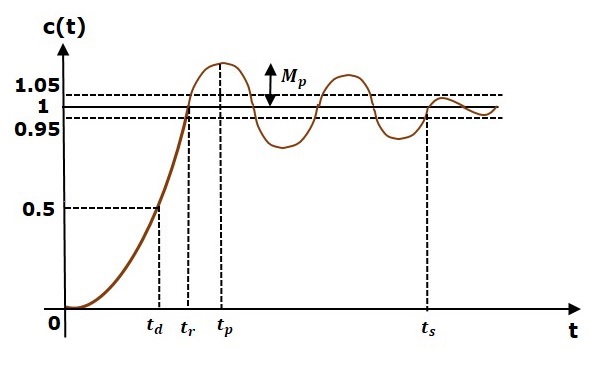
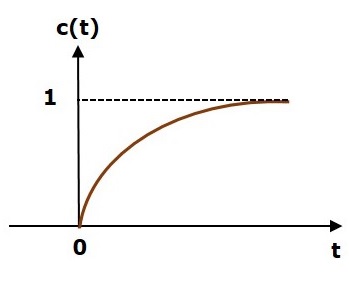
Реакция системы управления во временной области показана на следующем рисунке.

Здесь как переходные, так и стационарные состояния указаны на рисунке. Ответы, соответствующие этим состояниям, известны как ответы переходного и стационарного состояний.

Математически мы можем записать временную характеристику c (t) как

$$C (T) = C_ {тр} (т) + C_ {сс} (т)$$

Куда,

• c _tr (t) — переходный ответ
• c _ss (t) — реакция устойчивого состояния

Переходный ответ

После подачи ввода в систему управления, выходу требуется определенное время для достижения устойчивого состояния. Таким образом, выходной сигнал будет в переходном состоянии, пока он не перейдет в устойчивое состояние. Следовательно, ответ системы управления во время переходного состояния называется переходным процессом .

Переходный отклик будет нулевым для больших значений «t». В идеале это значение ‘t’ равно бесконечности и практически в пять раз больше.

Математически мы можем записать это как

$$\ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0$$

Устойчивый государственный ответ

Часть временного отклика, которая остается даже после переходного отклика, имеет нулевое значение для больших значений «t», называется устойчивым откликом . Это означает, что переходный отклик будет нулевым даже в установившемся режиме.

пример

Найдем нестационарные и установившиеся состояния временной реакции системы управления $c (t) = 10 + 5e ^ {- t}$

Здесь второе слагаемое $5e ^ {- t}$ будет равно нулю, так как t обозначает бесконечность. Итак, это переходный термин . И первый член 10 остается даже при приближении t к бесконечности. Итак, это термин устойчивого состояния .

Стандартные тестовые сигналы

Стандартные тестовые сигналы: импульсный, шаговый, линейный и параболический. Эти сигналы используются для определения производительности систем управления с использованием временной характеристики выхода.

Импульсный сигнал блока

Единичный импульсный сигнал δ (t) определяется как

$\ delta (t) = 0$ для $t \ neq 0$

и $\ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1$

На следующем рисунке показан единичный импульсный сигнал.

Итак, единичный импульсный сигнал существует только при ‘t’, равном нулю. Площадь этого сигнала при небольшом интервале времени вокруг ‘t’ равна нулю и равна единице. Значение единичного импульсного сигнала равно нулю для всех остальных значений «t».

Сигнал шага блока

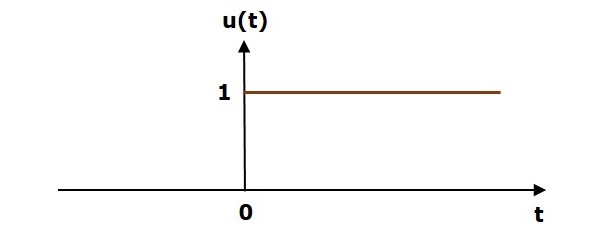
Единичный шаговый сигнал u (t) определяется как

$$u (t) = 1; t \ geq 0$$

$ = 0; т <0 $

На следующем рисунке показан сигнал шага блока.

Таким образом, сигнал единичного шага существует для всех положительных значений ‘t’, включая ноль. И его значение равно единице за этот интервал. Значение сигнала единичного шага равно нулю для всех отрицательных значений ‘t’.

Сигнал рампы

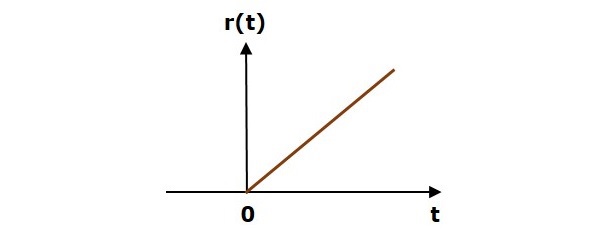
Сигнал линейного изменения r (t) определяется как

$$ R (T) = т; t \ geq 0 $$

$ = 0; т <0 $

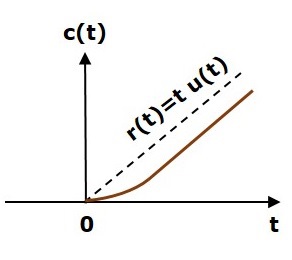
Мы можем записать единичный сигнал линейного изменения, $r (t)$ через единичный сигнал шага, $u (t)$ как

$$R (T) = TU (T)$$

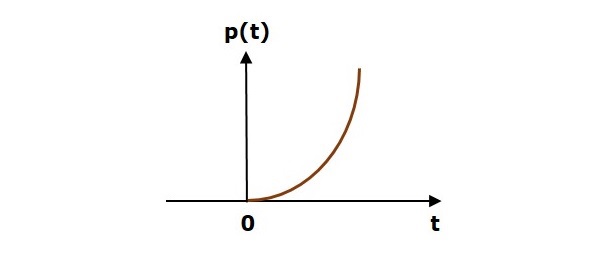
На следующем рисунке показан сигнал линейного изменения.

Таким образом, сигнал линейного изменения существует для всех положительных значений ‘t’, включая ноль. И его значение увеличивается линейно по отношению к ‘t’ в течение этого интервала. Значение единичного сигнала линейного изменения равно нулю для всех отрицательных значений ‘t’.

Единичный параболический сигнал

Единичный параболический сигнал p (t) определяется как,

$$ р (т) = \ гидроразрыва {т ^ 2} {2}; t \ geq 0 $$

$ = 0; т <0 $

Мы можем записать единичный параболический сигнал, $p (t)$ через единичный сигнал шага, $u (t)$ как,

$$р (т) = \ гидроразрыва {т ^ 2} {2} и (т)$$

На следующем рисунке показан блок параболического сигнала.

Таким образом, единичный параболический сигнал существует для всех положительных значений ‘t’, включая ноль. И его значение увеличивается нелинейно по отношению к ‘t’ в течение этого интервала. Значение единичного параболического сигнала равно нулю для всех отрицательных значений ‘t’.

Ответ системы первого заказа

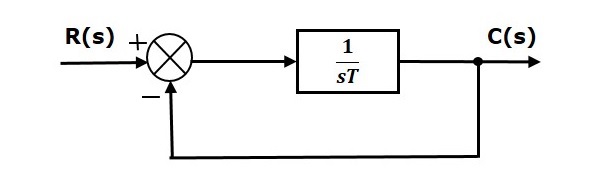
В этой главе давайте обсудим временную характеристику системы первого порядка. Рассмотрим следующую блок-схему замкнутой системы управления. Здесь передаточная функция без обратной связи $\ frac {1} {sT}$ связана с единственной отрицательной обратной связью.

Мы знаем, что передаточная функция замкнутой системы управления имеет единую отрицательную обратную связь, как,

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {G (s)} {1 + G (s)}$$

Замените $G (s) = \ frac {1} {sT}$ в приведенном выше уравнении.

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ гидроразрыва {1} {St}} {1+ \ гидроразрыва {1} {St}} = \ гидроразрыва {1} {ST + 1}$$

Степень s равна единице в знаменателе. Следовательно, вышеупомянутая передаточная функция имеет первый порядок, и система называется системой первого порядка .

Мы можем переписать приведенное выше уравнение как

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$$

Куда,

• C (s) — преобразование Лапласа выходного сигнала c (t),

• R (s) — преобразование Лапласа входного сигнала r (t), и

• Т — постоянная времени.

C (s) — преобразование Лапласа выходного сигнала c (t),

R (s) — преобразование Лапласа входного сигнала r (t), и

Т — постоянная времени.

Выполните следующие действия, чтобы получить ответ (вывод) системы первого порядка во временной области.

• Возьмем преобразование Лапласа входного сигнала $r (t)$.

• Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

• Замените значение $R (s)$ в приведенном выше уравнении.

• Делайте частичные дроби $C (s)$, если требуется.

• Примените обратное преобразование Лапласа к $C (s)$.

Возьмем преобразование Лапласа входного сигнала $r (t)$.

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените значение $R (s)$ в приведенном выше уравнении.

Делайте частичные дроби $C (s)$, если требуется.

Примените обратное преобразование Лапласа к $C (s)$.

В предыдущей главе мы видели стандартные тестовые сигналы, такие как импульс, шаг, линейное изменение и параболический сигнал. Давайте теперь выясним ответы системы первого порядка для каждого входа, один за другим. Имя ответа дается в соответствии с именем входного сигнала. Например, отклик системы на импульсный вход называется импульсным откликом.

Импульсный отклик системы первого порядка

Рассмотрим импульсный сигнал устройства как вход в систему первого порядка.

Итак, $r (t) = \ delta (t)$

Примените преобразование Лапласа с обеих сторон.

$R (s) = 1$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = 1$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) (1) = \ frac {1} {sT + 1}$$

Переставьте приведенное выше уравнение в одну из стандартных форм преобразований Лапласа.

$$C (s) = \ frac {1} {T \ left (\ s + \ frac {1} {T} \ right)} \ Rightarrow C (s) = \ frac {1} {T} \ left (\ frac {1} {s + \ frac {1} {T}} \ right)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ frac {1} {T} e ^ \ left ({- \ frac {t} {T}} \ right) u (t)$$

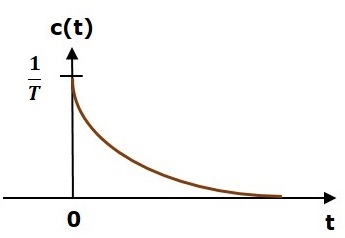
Импульсная характеристика устройства показана на следующем рисунке.

Единичная импульсная характеристика , c (t), представляет собой экспоненциальный затухающий сигнал для положительных значений «t», и он равен нулю для отрицательных значений «t».

Шаговая реакция системы первого заказа

Рассмотрим сигнал единичного шага как вход в систему первого порядка.

Итак, $r (t) = u (t)$

Примените преобразование Лапласа с обеих сторон.

$$R (s) = \ гидроразрыва {1} {s}$$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s} \ right) = \ frac {1} {s \ left (sT + 1 \ right)}$$

Делаем частичные дроби из C (s).

$$C (s) = \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1}$$

$$\ Rightarrow \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A \ left (sT + 1 \ right) + Bs} {s \ left (sT + 1 \ right)}$$

Обе стороны знаменателя одинаковы. Таким образом, они будут отменены друг другом. Следовательно, приравнивайте члены числителя.

$$1 = A \ left (sT + 1 \ right) + Bs$$

Приравнивая постоянные члены с обеих сторон, вы получите A = 1.

Подставим A = 1 и уравняем коэффициент слагаемых с обеих сторон.

$$0 = T + B \ Rightarrow B = -T$$

Подставим, A = 1 и B = −T при частичном разложении в $C (s)$.

$$C (s) = \ frac {1} {s} - \ frac {T} {sT + 1} = \ frac {1} {s} - \ frac {T} {T \ left (s + \ frac { 1} {T} \ right)}$$

$$\ Rightarrow C (s) = \ frac {1} {s} - \ frac {1} {s + \ frac {1} {T}}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (1-e ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t)$$

Реакция на единичный шаг c (t) имеет как переходные, так и установившиеся состояния.

Переходный член в ответе на единичный шаг —

$$c_ {tr} (t) = - e ^ {- \ left (\ frac {t} {T} \ right)} u (t)$$

Термин установившегося состояния в ответе шага блока —

$$C_ {сс} (т) = и (т)$$

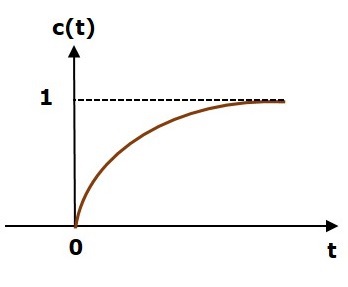
На следующем рисунке показан ответ шага устройства.

Значение единичного шага отклика c (t) равно нулю при t = 0 и для всех отрицательных значений t. Он постепенно увеличивается от нулевого значения и, наконец, достигает единицы в устойчивом состоянии. Таким образом, значение установившегося состояния зависит от величины входного сигнала.

Реакция системы первого порядка

Рассмотрим сигнал линейного изменения в качестве входа в систему первого порядка.

$Итак, r (t) = tu (t)$

Примените преобразование Лапласа с обеих сторон.

$$R (s) = \ гидроразрыва {1} {s ^ 2}$$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = \ frac {1} {s ^ 2}$ в вышеприведенном уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 2} \ right) = \ frac {1} {s ^ 2 ( ST + 1)}$$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {1} {s ^ 2 (ST + 1)} = \ гидроразрыва {A}, {s ^ 2} + \ гидроразрыва {B}, {s} + \ гидроразрыва {C}, {St +1}$$

$$\ Rightarrow \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A (sT + 1) + Bs (sT + 1) + Cs ^ 2} {s ^ 2 (sT + 1) }$$

Обе стороны знаменателя одинаковы. Таким образом, они будут отменены друг другом. Следовательно, приравнивайте члены числителя.

$$1 = А (St + 1) Bs (ST + 1) + Cs ^ 2$$

Приравнивая постоянные члены с обеих сторон, вы получите A = 1.

Подставим A = 1 и уравняем коэффициент слагаемых с обеих сторон.

$$0 = T + B \ Rightarrow B = -T$$

Аналогично подставьте B = −T и приравните коэффициент слагаемых $s ^ 2$ с обеих сторон. Вы получите $C = T ^ 2$.

Замените A = 1, B = −T и $C = T ^ 2$ в разложении по частям в $C (s)$.

$$C (S) = \ гидроразрыва {1} {s ^ 2} - \ гидроразрыва {T}, {s} + \ гидроразрыва {Т ^ 2} {ST + 1} = \ гидроразрыва {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {T \ left (s + \ frac {1} {T} \ right)}$$

$$\ Rightarrow C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (t-T + Te ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t)$$

Реакция единичного изменения , c (t), имеет как переходные, так и установившиеся состояния.

Переходный член в отклике линейного изменения —

$$c_ {tr} (t) = Te ^ {- \ left (\ frac {t} {T} \ right)} u (t)$$

Термин установившегося состояния в ответе линейного изменения —

$$C_ {сс} (т) = (Tt) и (г)$$

На следующем рисунке показан ответ линейного изменения.

Реакция единичного изменения , c (t), следует за входным сигналом линейного изменения для всех положительных значений t. Но есть отклонение T единиц от входного сигнала.

Параболический ответ системы первого порядка

Рассмотрим единичный параболический сигнал как вход в систему первого порядка.

Итак, $r (t) = \ frac {t ^ 2} {2} u (t)$

Примените преобразование Лапласа с обеих сторон.

$$R (s) = \ гидроразрыва {1} {s ^ 3}$$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = \ frac {1} {s ^ 3}$ в вышеприведенном уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 3} \ right) = \ frac {1} {s ^ 3 ( ST + 1)}$$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {1} {s ^ 3 (ST + 1)} = \ гидроразрыва {A}, {s ^ 3} + \ гидроразрыва {B}, {s ^ 2} + \ гидроразрыва {C} {s} + \ гидроразрыва {D} {ST + 1}$$

После упрощения вы получите значения A, B, C и D как 1, $-T, \: T ^ 2 \: и \: −T ^ 3$ соответственно. Подставьте эти значения в приведенное выше частичное расширение доли C (s).

$C (S) = \ гидроразрыва {1} {s ^ 3} - \ гидроразрыва {T}, {s ^ 2} + \ гидроразрыва {Т ^ 2} {s} - \ гидроразрыва {Т ^ 3} {ST + 1 } \: \ Rightarrow C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 2} {s + \ гидроразрыва {1} {T}}$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} \ right ) и (г)$$

Единичный параболический отклик c (t) имеет как переходные, так и стационарные условия.

Переходный член в единичном параболическом ответе

$$C_ {tr} (t) = - T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} u (t)$$

Член стационарного состояния в единичном параболическом ответе равен

$$C_ {ss} (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2 \ right) u (t)$$

Из этих ответов мы можем сделать вывод, что системы управления первого порядка нестабильны с линейными и параболическими входами, потому что эти реакции продолжают увеличиваться даже в бесконечное количество времени. Системы управления первого порядка стабильны с импульсными и шаговыми входами, потому что эти отклики имеют ограниченный выход. Но импульсный отклик не имеет устойчивого состояния. Таким образом, шаговый сигнал широко используется во временной области для анализа систем управления по их откликам.

Ответ системы второго порядка

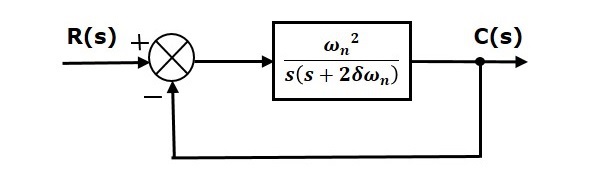
В этой главе давайте обсудим временную характеристику системы второго порядка. Рассмотрим следующую блок-схему замкнутой системы управления. Здесь передаточная функция с разомкнутым контуром, $\ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)}$, связана с единственной отрицательной обратной связью.

Известно, что передаточная функция замкнутой системы управления, имеющей единичную отрицательную обратную связь, равна

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {G (s)} {1 + G (s)}$$

Замените $G (s) = \ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)}$ в вышеприведенном уравнении.

$$\ frac {C (s)} {R (s)} = \ frac {\ left (\ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)} \ right)} {1+ \ left (\ frac {\ omega ^ 2_n} {s (s + 2 \ delta \ omega_n)} \ right)} = \ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega _ns + \ omega _n ^ 2}$$

Сила ‘s’ — это два в знаменателе. Следовательно, вышеупомянутая передаточная функция имеет второй порядок, и система называется системой второго порядка .

Характеристическое уравнение —

$$s ^ 2 + 2 \ delta \ omega _ns + \ omega _n ^ 2 = 0$$

Корни характеристического уравнения —

$$s = \ frac {-2 \ omega \ delta _n \ pm \ sqrt {(2 \ delta \ omega _n) ^ 2-4 \ omega _n ^ 2}} {2} = \ frac {-2 (\ delta \ omega _n \ pm \ omega _n \ sqrt {\ delta ^ 2-1})} {2}$$

$$\ Rightarrow s = - \ delta \ omega_n \ pm \ omega _n \ sqrt {\ delta ^ 2-1}$$

• Два корня мнимые, когда δ = 0.
• Два корня действительны и равны, когда δ = 1.
• Два корня действительны, но не равны, когда δ> 1.
• Два корня являются комплексно сопряженными, когда 0 <δ <1.

Мы можем написать уравнение $C (s)$ как,

$$C (s) = \ left (\ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2} \ right) R (s)$$

Куда,

• C (s) — преобразование Лапласа выходного сигнала, c (t)

• R (s) — преобразование Лапласа входного сигнала, r (t)

• ω _n — собственная частота

• δ — коэффициент демпфирования.

C (s) — преобразование Лапласа выходного сигнала, c (t)

R (s) — преобразование Лапласа входного сигнала, r (t)

ω _n — собственная частота

δ — коэффициент демпфирования.

Выполните следующие действия, чтобы получить ответ (вывод) системы второго порядка во временной области.

• Возьмем преобразование Лапласа входного сигнала, $r (t)$.

• Рассмотрим уравнение, $C (s) = \ left (\ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2} \ right) R (s)$

• Замените значение $R (s)$ в приведенном выше уравнении.

• Делайте частичные дроби $C (s)$, если требуется.

• Примените обратное преобразование Лапласа к $C (s)$.

Возьмем преобразование Лапласа входного сигнала, $r (t)$.

Рассмотрим уравнение, $C (s) = \ left (\ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2} \ right) R (s)$

Замените значение $R (s)$ в приведенном выше уравнении.

Делайте частичные дроби $C (s)$, если требуется.

Примените обратное преобразование Лапласа к $C (s)$.

Шаговая реакция системы второго порядка

Рассмотрим сигнал единичного шага в качестве входа в систему второго порядка.

Преобразование Лапласа единичного сигнала шага,

$$R (s) = \ гидроразрыва {1} {s}$$

Мы знаем, что передаточная функция замкнутой системы управления второго порядка:

$$\ frac {C (s)} {R (s)} = \ frac {\ omega _n ^ 2} {s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2}$$

Случай 1: δ = 0

Подставьте $\ delta = 0$ в передаточную функцию.

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {s ^ 2 + \ omega_n ^ 2}$$

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {s ^ 2 + \ omega_n ^ 2} \ right) R (s)$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {\ omega_n ^ 2} {s ^ 2 + \ omega_n ^ 2} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s (s ^ 2 + \ omega_n ^ 2)}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (1- \ cos (\ omega_n t) \ right) u (t)$$

Таким образом, отклик единичного шага системы второго порядка, когда $/ delta = 0$, будет непрерывным сигналом времени с постоянной амплитудой и частотой.

Случай 2: δ = 1

Замените $/ delta = 1$ в передаточной функции.

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {s ^ 2 + 2 \ omega_ns + \ omega_n ^ 2}$$

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ omega_n) ^ 2} \ right) R (s)$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ omega_n) ^ 2} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s (s + \ omega_n) ^ 2}$$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {\ omega_n ^ 2} {S (S + \ omega_n) ^ 2} = \ гидроразрыва {A}, {s} + \ гидроразрыва {B}, {S + \ omega_n} + \ гидроразрыва {С } {(s + \ omega_n) ^ 2}$$

После упрощения вы получите значения A, B и C как $1, \: -1 \: и \: - \ omega _n$ соответственно. Подставьте эти значения в приведенное выше частичное дробное выражение $C (s)$.

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {1} {S + \ omega_n} - \ гидроразрыва {\ omega_n} {(з + \ omega_n) ^ 2}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = (1-e ^ {- \ omega_nt} - \ omega _nte ^ {- \ omega_nt}) u (t)$$

Таким образом, единичный шаговый отклик системы второго порядка будет пытаться достичь пошагового ввода в устойчивом состоянии.

Случай 3: 0 <δ <1

Мы можем изменить знаменатель члена передаточной функции следующим образом:

$$s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2 = \ left \ {s ^ 2 + 2 (s) (\ delta \ omega_n) + (\ delta \ omega_n) ^ 2 \ right \} + \ omega_n ^ 2 - (\ Delta \ omega_n) ^ 2$$

$$= (S + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)$$

Передаточная функция становится,

$$ \ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)} $ $

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2)} \ right) R (s )$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$ C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2)} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s \ left ((s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2) \ right)} $ $

Делаем частичные дроби $C (s)$.

$$C (s) = \ frac {\ omega_n ^ 2} {s \ left ((s + \ delta \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ delta ^ 2) \ right)} = \ frac { А} {s} + \ гидроразрыва {Bs + С} {(s + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)}$$

После упрощения вы получите значения A, B и C как $1, \: -1 \: и \: −2 \ delta \ omega _n$ соответственно. Подставьте эти значения в приведенное выше частичное расширение доли C (s).

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {S + 2 \ дельта \ omega_n} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2) }$$

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {S + \ дельта \ omega_n} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)} - \ гидроразрыва {\ Delta \ omega_n} {(з + \ дельта \ omega_n) ^ 2 + \ omega_n ^ 2 (1- \ дельта ^ 2)}$$

$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {(S + \ дельта \ omega_n)} {(з + \ дельта \ omega_n) ^ 2 + (\ omega_n \ SQRT {1- \ дельта ^ 2} ) ^ 2} - \ frac {\ delta} {\ sqrt {1- \ delta ^ 2}} \ left (\ frac {\ omega_n \ sqrt {1- \ delta ^ 2}}} ((s + \ delta \ omega_n) ^ 2 + (\ omega_n \ sqrt {1- \ delta ^ 2}) ^ 2} \ right)$

Замените $\ omega_n \ sqrt {1- \ delta ^ 2}$ на $\ omega_d$ в вышеприведенном уравнении.

$$C (S) = \ гидроразрыва {1} {s} - \ гидроразрыва {(S + \ дельта \ omega_n)} {(з + \ дельта \ omega_n) ^ 2 + \ omega_d ^ 2} - \ гидроразрыва {\ Delta} {\ sqrt {1- \ delta ^ 2}} \ left (\ frac {\ omega_d} {(s + \ delta \ omega_n) ^ 2 + \ omega_d ^ 2} \ right)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (1-e ^ {- \ delta \ omega_nt} \ cos (\ omega_dt) - \ frac {\ delta} {\ sqrt {1- \ delta ^ 2}} e ^ {- \ delta \ omega_nt} \ sin (\ omega_dt) \ right) u (t)$$

$$c (t) = \ left (1- \ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ left ((\ sqrt {1- \ delta ^ 2 }) \ cos (\ omega_dt) + \ delta \ sin (\ omega_dt) \ right) \ right) u (t)$$

Если $\ sqrt {1- \ delta ^ 2} = \ sin (\ theta)$, то δ будет cos (θ). Подставьте эти значения в приведенное выше уравнение.

$$c (t) = \ left (1- \ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} (\ sin (\ theta) \ cos (\ omega_dt) + \ cos (\ theta) \ sin (\ omega_dt)) \ right) u (t)$$

$$\ Rightarrow c (t) = \ left (1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta) \ right) u (t)$$

Таким образом, отклик единичного шага системы второго порядка имеет затухающие колебания (уменьшение амплитуды), когда «δ» лежит между нулем и единицей.

Случай 4: δ> 1

Мы можем изменить знаменатель члена передаточной функции следующим образом:

$$s ^ 2 + 2 \ delta \ omega_ns + \ omega_n ^ 2 = \ left \ {s ^ 2 + 2 (s) (\ delta \ omega_n) + (\ delta \ omega_n) ^ 2 \ right \} + \ omega_n ^ 2 - (\ Delta \ omega_n) ^ 2$$

$$= \ left (s + \ delta \ omega_n \ right) ^ 2- \ omega_n ^ 2 \ left (\ delta ^ 2-1 \ right)$$

Передаточная функция становится,

$$ \ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ omega_n ^ 2} {(з + \ дельта \ omega_n) ^ 2- \ omega_n ^ 2 (\ дельта ^ 2-1)} $ $

$$\ Rightarrow C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2- \ omega_n ^ 2 (\ delta ^ 2-1)} \ right) R (s) )$$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$C (s) = \ left (\ frac {\ omega_n ^ 2} {(s + \ delta \ omega_n) ^ 2 - (\ omega_n \ sqrt {\ delta ^ 2-1}) ^ 2} \ right) \ left (\ frac {1} {s} \ right) = \ frac {\ omega_n ^ 2} {s (s + \ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}) (s + \ delta \ omega_n- \ omega_n \ SQRT {\ Delta ^ 2-1})}$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {\ omega_n ^ 2} {S (S + \ дельта \ omega_n + \ omega_n \ SQRT {\ Delta ^ 2-1}) (S + \ Delta \ omega_n- \ omega_n \ SQRT {\ дельта ^ 2-1})}$$

$$= \ гидроразрыва {A}, {s} + \ гидроразрыва {B}, {S + \ дельта \ omega_n + \ omega_n \ SQRT {\ Delta ^ 2-1}} + \ гидроразрыва {C}, {S + \ Delta \ omega_n- \ omega_n \ SQRT {\ Delta ^ 2-1}}$$

После упрощения вы получите значения A, B и C как 1, $\ frac {1} {2 (\ delta + \ sqrt {\ delta ^ 2-1}) (\ sqrt {\ delta ^ 2-1} )}$ и $\ frac {-1} {2 (\ delta- \ sqrt {\ delta ^ 2-1}) (\ sqrt {\ delta ^ 2-1})}$ соответственно. Подставьте эти значения в приведенное выше частичное дробное разложение $C (s)$.

$$C (S) = \ гидроразрыва {1} {s} + \ гидроразрыва {1} {2 (\ Delta + \ SQRT {\ Delta ^ 2-1}) (\ SQRT {\ Delta ^ 2-1})} \ left (\ frac {1} {s + \ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}} \ right) - \ left (\ frac {1} {2 (\ delta- \ sqrt {\ delta) ^ 2-1}) (\ sqrt {\ delta ^ 2-1})} \ right) \ left (\ frac {1} {s + \ delta \ omega_n- \ omega_n \ sqrt {\ delta ^ 2-1}} \ право)$$

Примените обратное преобразование Лапласа с обеих сторон.

$c (t) = \ left (1+ \ left (\ frac {1} {2 (\ delta + \ sqrt {\ delta ^ 2-1}) (\ sqrt {\ delta ^ 2-1})}} right ) e ^ {- (\ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}) t} - \ left (\ frac {1} {2 (\ delta- \ sqrt {\ delta ^ 2-1} ) (\ sqrt {\ delta ^ 2-1})} \ right) e ^ {- (\ delta \ omega_n- \ omega_n \ sqrt {\ delta ^ 2-1}) t} \ right) u (t)$

Поскольку он слишком демпфирован, отклик единичного шага системы второго порядка, когда δ> 1, никогда не достигнет шага ввода в установившемся режиме.

Импульсный отклик системы второго порядка

Импульсная характеристика системы второго порядка может быть получена с помощью любого из этих двух методов.

• При получении ответа на шаг следуйте процедуре, рассматривая значение $R (s)$ как 1 вместо $\ frac {1} {s}$.

• Сделайте дифференциацию шага ответа.

При получении ответа на шаг следуйте процедуре, рассматривая значение $R (s)$ как 1 вместо $\ frac {1} {s}$.

Сделайте дифференциацию шага ответа.

В следующей таблице приведены импульсные характеристики системы второго порядка для 4 случаев коэффициента демпфирования.

Состояние коэффициента демпфирования	Импульсный отклик при t ≥ 0
δ = 0	$\ Omega_n \ sin (\ omega_nt)$
δ = 1	$\ Omega_n ^ 2TE ^ {- \ omega_nt}$
0 <δ <1	$\ left (\ frac {\ omega_ne ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt)$
δ> 1	$\ left (\ frac {\ omega_n} {2 \ sqrt {\ delta ^ 2-1}} \ right) \ left (e ^ {- (\ delta \ omega_n- \ omega_n \ sqrt {\ delta ^ 2-1) }) t} -e ^ {- (\ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}) t} \ right)$

δ = 0

$\ Omega_n \ sin (\ omega_nt)$

δ = 1

$\ Omega_n ^ 2TE ^ {- \ omega_nt}$

0 <δ <1

$\ left (\ frac {\ omega_ne ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt)$

δ> 1

$\ left (\ frac {\ omega_n} {2 \ sqrt {\ delta ^ 2-1}} \ right) \ left (e ^ {- (\ delta \ omega_n- \ omega_n \ sqrt {\ delta ^ 2-1) }) t} -e ^ {- (\ delta \ omega_n + \ omega_n \ sqrt {\ delta ^ 2-1}) t} \ right)$

Спецификации временной области

В этой главе давайте обсудим спецификации временной области системы второго порядка. Ответ шага системы второго порядка для случая недостаточной амортизации показан на следующем рисунке.

Все спецификации домена времени представлены на этом рисунке. Отклик до времени установления известен как переходный отклик, а отклик после времени установления называется устойчивым откликом.

Время задержки

Это время, необходимое для того, чтобы ответ достиг половины своего окончательного значения с нулевого момента. Обозначается $t_d$.

Рассмотрим пошаговый отклик системы второго порядка для t ≥ 0, когда δ лежит между нулем и единицей.

$$c (t) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta)$$

Окончательное значение шага ответа равно единице.

Следовательно, при $t = t_d$ значение шага отклика будет 0,5. Подставим эти значения в приведенное выше уравнение.

$$c (t_d) = 0.5 = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt_d}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_d + \ theta)$$

$$\ Rightarrow \ left (\ frac {e ^ {- \ delta \ omega_nt_d}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_d + \ theta) = 0,5$$

Используя линейное приближение, вы получите время задержки t _d как

$$T_d = \ гидроразрыва {1 + 0,7 \ дельта} {\ omega_n}$$

Время нарастания

Это время, необходимое для отклика, чтобы подняться с 0% до 100% от его окончательного значения . Это применимо для систем с недостаточным демпфированием . Для систем с избыточным демпфированием учитывайте продолжительность от 10% до 90% от окончательного значения. Время подъема обозначается через t _r .

При t = t ₁ = 0, c (t) = 0.

Мы знаем, что окончательное значение шага ответа равно единице.

Следовательно, при $t = t_2$ значение шага отклика равно единице. Подставим эти значения в следующее уравнение.

$$c (t) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta)$$

$$c (t_2) = 1 = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt_2}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_2 + \ theta)$$

$$\ Rightarrow \ left (\ frac {e ^ {- \ delta \ omega_nt_2}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_2 + \ theta) = 0$$

$$\ Rightarrow \ sin (\ omega_dt_2 + \ theta) = 0$$

$$\ Rightarrow \ omega_dt_2 + \ theta = \ pi$$

$$\ Rightarrow t_2 = \ frac {\ pi- \ theta} {\ omega_d}$$

Подставим значения t ₁ и t ₂ в следующее уравнение времени нарастания ,

$$t_r = t_2-t_1$$

$$\ Следовательно \: t_r = \ frac {\ pi- \ theta} {\ omega_d}$$

Из приведенного выше уравнения можно сделать вывод, что время нарастания $t_r$ и затухающая частота $\ omega_d$ обратно пропорциональны друг другу.

Час пик

Это время, необходимое для ответа, чтобы достичь пикового значения в первый раз. Обозначается $t_p$. При $t = t_p$ первый производный ответа равен нулю.

Мы знаем, что пошаговый отклик системы второго порядка для случая недостаточного затухания

$$c (t) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta)$$

Продифференцируйте $c (t)$ относительно ‘t’.

$$\ frac {\ text {d} c (t)} {\ text {d} t} = - \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ omega_d \ cos (\ omega_dt + \ theta) - \ left (\ frac {- \ delta \ omega_ne ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ справа) \ sin (\ omega_dt + \ theta)$$

Замените $t = t_p$ и $\ frac {\ text {d} c (t)} {\ text {d} t} = 0$ в вышеприведенном уравнении.

$$0 = - \ left (\ frac {e ^ {- \ delta \ omega_nt_p}} {\ sqrt {1- \ delta ^ 2}} \ right) \ left [\ omega_d \ cos (\ omega_dt_p + \ theta) - \ delta \ omega_n \ sin (\ omega_dt_p + \ theta) \ right]$$

$$\ Rightarrow \ omega_n \ sqrt {1- \ delta ^ 2} \ cos (\ omega_dt_p + \ theta) - \ delta \ omega_n \ sin (\ omega_dt_p + \ theta) = 0$$

$$\ Rightarrow \ sqrt {1- \ delta ^ 2} \ cos (\ omega_dt_p + \ theta) - \ delta \ sin (\ omega_dt_p + \ theta) = 0$$

$$\ Rightarrow \ sin (\ theta) \ cos (\ omega_dt_p + \ theta) - \ cos (\ theta) \ sin (\ omega_dt_p + \ theta) = 0$$

$$\ Rightarrow \ sin (\ theta- \ omega_dt_p- \ theta) = 0$$

$$\ Rightarrow sin (- \ omega_dt_p) = 0 \ Rightarrow - \ sin (\ omega_dt_p) = 0 \ Rightarrow sin (\ omega_dt_p) = 0$$

$$\ Rightarrow \ omega_dt_p = \ pi$$

$$\ Rightarrow t_p = \ frac {\ pi} {\ omega_d}$$

Из приведенного выше уравнения можно сделать вывод, что время пика $t_p$ и затухающая частота $\ omega_d$ обратно пропорциональны друг другу.

Пик Overshoot

Пик перерегулирования M _p определяется как отклонение отклика в пиковое время от конечного значения отклика. Это также называется максимальным выбросом .

Математически мы можем записать это как

$$m_p = с (t_p) -c (\ infty)$$

Куда,

c (t _p ) — пиковое значение ответа.

c (∞) — окончательное (установившееся) значение ответа.

При $t = t_p$ ответ c (t) равен —

$$c (t_p) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt_p}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_p + \ theta)$$

Замените $t_p = \ frac {\ pi} {\ omega_d}$ в правой части вышеприведенного уравнения.

$$c (t_P) = 1- \ left (\ frac {e ^ {- \ delta \ omega_n \ left (\ frac {\ pi} {\ omega_d} \ right)}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin \ left (\ omega_d \ left (\ frac {\ pi} {\ omega_d} \ right) + \ theta \ right)$$

$$\ Rightarrow c (t_p) = 1- \ left (\ frac {e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)}} { \ sqrt {1- \ delta ^ 2}} \ right) (- \ sin (\ theta))$$

Мы знаем это

$$\ Sin (\ Theta) = \ SQRT {1- \ дельта ^ 2}$$

Итак, мы получим $c (t_p)$ как

$$c (t_p) = 1 + e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)}$$

Подставьте значения $c (t_p)$ и $c (\ infty)$ в уравнение выброса пика.

$$M_p = 1 + e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} - ​​1$$

$$\ Rightarrow M_p = e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)}$$

Процент пикового перерегулирования% $M_p$ можно рассчитать с помощью этой формулы.

$$\% M_p = \ frac {M_p} {c (\ infty)} \ times 100 \%$$

Подставляя значения $M_p$ и $c (\ infty)$ в приведенную выше формулу, мы получим Процент превышения пика $\% M_p$ как

$$\% M_p = \ left (e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} \ right) \ times 100 \%$$

Из приведенного выше уравнения можно сделать вывод, что процент превышения пика $\% M_p$ уменьшится, если коэффициент демпфирования $\ delta$ увеличится.

Расчетное время

Это время, необходимое для того, чтобы ответ достиг установившегося состояния и остался в указанных пределах допуска около конечного значения. В общем, допустимые пределы составляют 2% и 5%. Время установления обозначается как $t_s$.

Время установления для диапазона допуска 5% —

$$t_s = \ гидроразрыва {3} {\ Delta \ omega_n} = 3 \ тау$$

Время установления для диапазона допуска 2% —

$$t_s = \ гидроразрыва {4} {\ Delta \ omega_n} = 4 \ тау$$

Где $\ tau$ — постоянная времени, равная $\ frac {1} {\ delta \ omega_n}$.

• И время установления $t_s$, и постоянная времени $\ tau$ обратно пропорциональны коэффициенту затухания $\ delta$.

• И время установления $t_s$, и постоянная времени $\ tau$ не зависят от усиления системы. Это означает, что даже прирост системы меняется, время установления $t_s$ и постоянная времени $\ tau$ никогда не изменятся.

И время установления $t_s$, и постоянная времени $\ tau$ обратно пропорциональны коэффициенту затухания $\ delta$.

И время установления $t_s$, и постоянная времени $\ tau$ не зависят от усиления системы. Это означает, что даже прирост системы меняется, время установления $t_s$ и постоянная времени $\ tau$ никогда не изменятся.

пример

Теперь давайте найдем спецификации временной области системы управления, имеющей передаточную функцию замкнутого контура $\ frac {4} {s ^ 2 + 2s + 4}$, когда сигнал единичного шага подается в качестве входа в эту систему управления.

Мы знаем, что стандартная форма передаточной функции замкнутой системы управления второго порядка в виде

$$\ гидроразрыва {\ omega_n ^ 2} {s ^ 2 + 2 \ Delta \ omega_ns + \ omega_n ^ 2}$$

Приравнивая эти две передаточные функции, мы получим естественную частоту $\ omega_n$ без демпфирования как 2 рад / с и коэффициент демпфирования $\ delta$ как 0,5.

Мы знаем формулу для затухающей частоты $\ omega_d$ как

$$\ omega_d = \ omega_n \ SQRT {1- \ дельта ^ 2}$$

Подставьте значения $\ omega_n$ и $\ delta$ в приведенной выше формуле.

$$\ Rightarrow \ omega_d = 2 \ sqrt {1- (0.5) ^ 2}$$

$$\ Rightarrow \ omega_d = 1.732 \: рад / с$$

Подставьте значение $\ delta$ в следующем соотношении

$$\ Theta = \ соз ^ {- 1} \ Delta$$

$$\ Rightarrow \ theta = \ cos ^ {- 1} (0.5) = \ frac {\ pi} {3} \: rad$$

Замените вышеуказанные необходимые значения в формуле каждой спецификации временной области и упростите, чтобы получить значения спецификаций временной области для данной передаточной функции.

В следующей таблице приведены формулы спецификаций временной области, подстановка необходимых значений и окончательных значений.

Спецификация временной области	формула	Подстановка значений в формуле	Конечное значение
Время задержки	$T_d = \ гидроразрыва {1 + 0,7 \ дельта} {\ omega_n}$	$T_d = \ гидроразрыва {1 + 0,7 (0,5)} {2}$	$t_d$ = 0,675 с
Время нарастания	$T_r = \ гидроразрыва {\ PI- \ Theta} {\}$ omega_d	$T_r = \ гидроразрыва {\ р - (\ гидроразрыва {\ Pi} {3})} {1,732}$	$t_r$ = 1,207 с
Час пик	$T_p = \ гидроразрыва {\ пи} {\}$ omega_d	$T_p = \ гидроразрыва {\ пи} {1,732}$	$t_p$ = 1,813 с
% Peak overshoot	$\% M_p = \ left (e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} \ right) \ times 100 \%$	$\% M_p = \ left (e ^ {- \ left (\ frac {0.5 \ pi} {\ sqrt {1- (0.5) ^ 2}} \ right)} \ right) \ times 100 \%$	$\% \: M_p$ = 16,32%
Время установления для диапазона допуска 2%	$T_s = \ гидроразрыва {4} {\ Delta \ omega_n}$	$T_S = \ гидроразрыва {4} {(0,5) (2)}$	$t_s$ = 4 сек

Время задержки

$T_d = \ гидроразрыва {1 + 0,7 \ дельта} {\ omega_n}$

$T_d = \ гидроразрыва {1 + 0,7 (0,5)} {2}$

$t_d$ = 0,675 с

Время нарастания

$T_r = \ гидроразрыва {\ PI- \ Theta} {\}$ omega_d

$T_r = \ гидроразрыва {\ р - (\ гидроразрыва {\ Pi} {3})} {1,732}$

$t_r$ = 1,207 с

Час пик

$T_p = \ гидроразрыва {\ пи} {\}$ omega_d

$T_p = \ гидроразрыва {\ пи} {1,732}$

$t_p$ = 1,813 с

% Peak overshoot

$\% M_p = \ left (e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} \ right) \ times 100 \%$

$\% M_p = \ left (e ^ {- \ left (\ frac {0.5 \ pi} {\ sqrt {1- (0.5) ^ 2}} \ right)} \ right) \ times 100 \%$

$\% \: M_p$ = 16,32%

Время установления для диапазона допуска 2%

$T_s = \ гидроразрыва {4} {\ Delta \ omega_n}$

$T_S = \ гидроразрыва {4} {(0,5) (2)}$

$t_s$ = 4 сек

Системы управления — ошибки стационарного состояния

Отклонение выхода системы управления от требуемого отклика в установившемся режиме называется ошибкой установившегося состояния . Он представлен как $e_ {ss}$. Мы можем найти ошибку стационарного состояния, используя теорему об окончательном значении, следующим образом.

$$e_ {ss} = \ lim_ {t \ to \ infty} e (t) = \ lim_ {s \ to 0} sE (s)$$

Куда,

E (s) — преобразование Лапласа сигнала ошибки, $e (t)$

Давайте обсудим, как находить ошибки установившегося состояния для систем управления с единой обратной связью и не единой обратной связи.

Ошибки установившегося состояния для систем обратной связи Unity

Рассмотрим следующую блок-схему замкнутой системы управления, которая имеет единую отрицательную обратную связь.

Куда,

• R (s) — преобразование Лапласа эталонного входного сигнала $r (t)$
• C (s) — преобразование Лапласа выходного сигнала $c (t)$

Мы знаем передаточную функцию замкнутой системы управления с отрицательной обратной связью как

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {G (s)} {1 + G (s)}$$

$$\ Rightarrow C (s) = \ frac {R (s) G (s)} {1 + G (s)}$$

Выход точки суммирования —

$$Е (с) = R (S) -C (ы)$$

Замените значение $C (s)$ в приведенном выше уравнении.

$$Е (ы) = R (S) - \ гидроразрыва {R (S) G (s)} {1 + G (s)}$$

$$\ Rightarrow E (s) = \ frac {R (s) + R (s) G (s) -R (s) G (s)} {1 + G (s)}$$

$$\ Rightarrow E (s) = \ frac {R (s)} {1 + G (s)}$$

Подставьте значение $E (s)$ в формулу ошибки стационарного состояния

$$e_ {ss} = \ lim_ {s \ to 0} \ frac {sR (s)} {1 + G (s)}$$

В следующей таблице показаны ошибки стационарного состояния и константы ошибок для стандартных входных сигналов, таких как шаг единицы измерения, линейное изменение скорости и единичные параболические сигналы.

Входной сигнал	Ошибка устойчивого состояния $e_ {ss}$	Постоянная ошибки
единичный шаговой сигнал	$\ Гидроразрыва {1} {1 + k_p}$	$K_p = \ lim_ {s \ to 0} G (s)$
сигнал рампы	$\ Гидроразрыва {1} {K_v}$	$K_v = \ lim_ {s \ to 0} сГ (с)$
единичный параболический сигнал	$\ Гидроразрыва {1} {K_a}$	$K_a = \ lim_ {s \ to 0} с ^ 2G (s)$

единичный шаговой сигнал

$\ Гидроразрыва {1} {1 + k_p}$

$K_p = \ lim_ {s \ to 0} G (s)$

сигнал рампы

$\ Гидроразрыва {1} {K_v}$

$K_v = \ lim_ {s \ to 0} сГ (с)$

единичный параболический сигнал

$\ Гидроразрыва {1} {K_a}$

$K_a = \ lim_ {s \ to 0} с ^ 2G (s)$

Где $K_p$, $K_v$ и $K_a$ — постоянная ошибки положения, постоянная ошибки скорости и постоянная ошибки ускорения соответственно.

Примечание. Если какой-либо из указанных выше входных сигналов имеет амплитуду, отличную от единицы, умножьте соответствующую ошибку установившегося состояния на эту амплитуду.

Примечание. Мы не можем определить ошибку установившегося состояния для импульсного сигнала устройства, поскольку он существует только в начале координат. Таким образом, мы не можем сравнивать импульсную характеристику с единичным импульсным входом, поскольку t обозначает бесконечность.

пример

Найдем ошибку установившегося состояния для входного сигнала $r (t) = \ left (5 + 2t + \ frac {t ^ 2} {2} \ right) u (t)$ единой системы управления отрицательной обратной связью с $G (с) = \ гидроразрыва {(5 + 4)} {s ^ 2 (s + 1) (s + 20)}$

Данный входной сигнал представляет собой комбинацию трех сигналов: ступенчатого, линейного и параболического. В следующей таблице приведены константы ошибок и значения ошибок установившегося состояния для этих трех сигналов.

Входной сигнал	Постоянная ошибки	Ошибка устойчивого состояния
$R_1 (т) = 5U (т)$	$K_p = \ lim_ {s \ to 0} G (s) = \ infty$	$E_ {SS1} = \ гидроразрыва {5} {1 + k_p} = 0$
$R_2 (т) = 2tu (т)$	$K_v = \ lim_ {s \ to 0} сГ (с) = \ infty$	{$E_ ss2} = \ гидроразрыва {2} {K_v} = 0$
$R_3 (т) = \ гидроразрыва {т ^ 2} {2} и (т)$	$K_a = \ lim_ {s \ to 0} с ^ 2G (s) = 1$	$E_ {ss3} = \ гидроразрыва {1} {k_a} = 1$

$R_1 (т) = 5U (т)$

$K_p = \ lim_ {s \ to 0} G (s) = \ infty$

$E_ {SS1} = \ гидроразрыва {5} {1 + k_p} = 0$

$R_2 (т) = 2tu (т)$

$K_v = \ lim_ {s \ to 0} сГ (с) = \ infty$

{$E_ ss2} = \ гидроразрыва {2} {K_v} = 0$

$R_3 (т) = \ гидроразрыва {т ^ 2} {2} и (т)$

$K_a = \ lim_ {s \ to 0} с ^ 2G (s) = 1$

$E_ {ss3} = \ гидроразрыва {1} {k_a} = 1$

Мы получим общую ошибку установившегося состояния, добавив три вышеуказанные ошибки установившегося состояния.

$$E_ {сс} = {е_ SS1} + е- {SS2} + е- {SS3}$$

$$\ Rightarrow e_ {ss} = 0 + 0 + 1 = 1$$

Таким образом, мы получили ошибку стационарного состояния $e_ {ss}$ как 1 для этого примера.

Ошибки установившегося состояния для систем с неединичной обратной связью

Рассмотрим следующую блок-схему замкнутой системы управления с отрицательной обратной связью.

Мы можем найти ошибки стационарного состояния только для систем с обратной связью. Таким образом, мы должны преобразовать систему неединой обратной связи в единую систему обратной связи. Для этого включите один единый путь положительной обратной связи и один единственный путь отрицательной обратной связи в приведенную выше блок-схему. Новая блок-схема выглядит так, как показано ниже.

Упростите приведенную выше блок-схему, сохранив единую отрицательную обратную связь как есть. Ниже приведена упрощенная блок-схема.

Эта блок-схема напоминает блок-схему единой системы управления с обратной связью с обратной связью. Здесь единственный блок имеет передаточную функцию $\ frac {G (s)} {1 + G (s) H (s) -G (s)}$ вместо $G (s)$. Теперь вы можете рассчитать ошибки установившегося состояния, используя формулу ошибки установившегося состояния, приведенную для систем единой отрицательной обратной связи.

Примечание. Бессмысленно находить ошибки стационарного состояния для неустойчивых систем с замкнутым контуром. Таким образом, мы должны вычислять ошибки стационарного состояния только для замкнутых систем. Это означает, что мы должны проверить, является ли система управления стабильной или нет, прежде чем обнаруживать ошибки установившегося состояния. В следующей главе мы обсудим концептуальную стабильность.

Системы управления — стабильность

Стабильность является важной концепцией. В этой главе давайте обсудим стабильность системы и типы систем, основанных на устойчивости.

Что такое стабильность?

Система называется стабильной, если ее выход находится под контролем. В противном случае он называется нестабильным. Стабильная система производит ограниченный вывод для данного ограниченного ввода.

На следующем рисунке показан ответ стабильной системы.

Это ответ системы управления первого порядка на шаговый ввод. Этот ответ имеет значения между 0 и 1. Таким образом, это ограниченный вывод. Мы знаем, что сигнал единичного шага имеет значение один для всех положительных значений t, включая ноль. Итак, это ограниченный ввод. Следовательно, система управления первого порядка стабильна, так как и вход, и выход ограничены.

Типы систем на основе стабильности

Мы можем классифицировать системы на основе стабильности следующим образом.

• Абсолютно стабильная система
• Условно стабильная система
• Маргинально стабильная система

Абсолютно стабильная система

Если система стабильна для всего диапазона значений системных компонентов, то она известна как абсолютно стабильная система . Система управления с разомкнутым контуром абсолютно устойчива, если все полюсы передаточной функции с разомкнутым контуром присутствуют в левой половине плоскости ‘s’ . Аналогично, система управления с обратной связью является абсолютно устойчивой, если все полюсы передаточной функции с обратной связью присутствуют в левой половине плоскости ‘s’.

Условно Стабильная Система

Если система стабильна для определенного диапазона значений компонентов системы, то она называется условно стабильной системой .

Стабильно стабильная система

Если система стабильна, создавая выходной сигнал с постоянной амплитудой и постоянной частотой колебаний для ограниченного входа, то она известна как предельно стабильная система . Система управления с разомкнутым контуром является минимально устойчивой, если на мнимой оси присутствуют любые два полюса передаточной функции с разомкнутым контуром. Аналогично, система управления с обратной связью является минимально устойчивой, если на мнимой оси присутствуют любые два полюса передаточной функции с обратной связью.

Системы управления — анализ устойчивости

В этой главе мы обсудим анализ устойчивости в области ‘s’ с использованием критерия устойчивости Роут-Гурвица. В этом критерии нам требуется характеристическое уравнение, чтобы найти устойчивость замкнутых систем управления.

Критерий устойчивости Рауса-Гурвица

Критерий устойчивости Рауса-Гурвица имеет одно необходимое условие и одно достаточное условие устойчивости. Если какая-либо система управления не удовлетворяет необходимым условиям, то можно сказать, что система управления нестабильна. Но если система управления удовлетворяет необходимому условию, то она может быть или не быть устойчивой. Таким образом, достаточное условие полезно для того, чтобы знать, является ли система управления стабильной или нет.

Необходимое условие устойчивости Рауса-Гурвица

Необходимым условием является то, что коэффициенты характеристического полинома должны быть положительными. Это означает, что все корни характеристического уравнения должны иметь отрицательные вещественные части.

Рассмотрим характеристическое уравнение порядка ‘n’ —

$$a_0s ^ п + a_1s ^ {N-1} + a_2s ^ {N-2} + ... а_ {п-1} с ^ 1 + a_ns ^ 0 = 0$$

Обратите внимание, что в характеристическом уравнении n- ^го порядка не должно быть пропущено ни одного члена. Это означает, что характеристическое уравнение n- ^го порядка не должно иметь никакого коэффициента, который имеет нулевое значение.

Достаточное условие стабильности Рауса-Гурвица

Достаточным условием является то, что все элементы первого столбца массива Routh должны иметь одинаковый знак. Это означает, что все элементы первого столбца массива Routh должны быть положительными или отрицательными.

Метод Routh Array

Если все корни характеристического уравнения существуют в левой половине плоскости ‘s’, то система управления устойчива. Если хотя бы один корень характеристического уравнения существует в правой половине плоскости ‘s’, то система управления неустойчива. Итак, мы должны найти корни характеристического уравнения, чтобы узнать, является ли система управления стабильной или нестабильной. Но трудно найти корни характеристического уравнения при увеличении порядка.

Итак, чтобы преодолеть эту проблему, у нас есть метод массива Routh . В этом методе нет необходимости вычислять корни характеристического уравнения. Сначала сформулируйте таблицу Рауса и найдите количество изменений знака в первом столбце таблицы Рауса. Число изменений знака в первом столбце таблицы Рауса дает число корней характеристического уравнения, которые существуют в правой половине плоскости ‘s’, а система управления неустойчива.

Выполните эту процедуру для формирования таблицы Рауса.

• Заполните первые две строки массива Рауса коэффициентами характеристического полинома, как указано в таблице ниже. Начните с коэффициента $s ^ n$ и продолжайте до коэффициента $s ^ 0$.

• Заполните оставшиеся строки массива Routh элементами, указанными в таблице ниже. Продолжайте этот процесс, пока не получите первый элемент столбца строки $ s ^ 0 $, равный$ a_n $. Здесь $a_n$ — коэффициент $s ^ 0$ в характеристическом полиноме.

Заполните первые две строки массива Рауса коэффициентами характеристического полинома, как указано в таблице ниже. Начните с коэффициента $s ^ n$ и продолжайте до коэффициента $s ^ 0$.

Заполните оставшиеся строки массива Routh элементами, указанными в таблице ниже. Продолжайте этот процесс, пока не получите первый элемент столбца строки $ s ^ 0 $, равный$ a_n $. Здесь $a_n$ — коэффициент $s ^ 0$ в характеристическом полиноме.

Примечание. Если у каких-либо элементов строки таблицы Routh есть какой-то общий фактор, вы можете разделить элементы строки с этим коэффициентом, чтобы упростить их было легко.

В следующей таблице показан массив Routh полинома характеристики n- ^го порядка.

$$a_0s ^ п + a_1s ^ {N-1} + a_2s ^ {N-2} + ... а_ {п-1} с ^ 1 + a_ns ^ 0$$

$S ^ п$	$A_0$	$A_2$	$A_4$	$A_6$	…	…
$S ^ {N-1}$	$A_1$	$A_3$	$A_5$	$A_7$	…	…
$S ^ {N-2}$	$B_1 = \ гидроразрыва {A_1A_2-a_3a_0} {a_1}$	$B_2 = \ гидроразрыва {a_1a_4-a_5a_0} {a_1}$	$B_3 = \ гидроразрыва {a_1a_6-a_7a_0} {a_1}$	…	…	…
$S ^ {п-3}$	$C_1 = \ гидроразрыва {b_1a_3-b_2a_1} {b_1}$	$C_2 = \ гидроразрыва {b_1a_55-b_3a_1} {b_1}$	$\ Vdots$
$\ vdots$	$\ Vdots$	$\ Vdots$	$\ Vdots$
$S ^ 1$	$\ Vdots$	$\ Vdots$
$S ^ 0$	$A_n$

$S ^ п$

$A_0$

$A_2$

$A_4$

$A_6$

…

…

$S ^ {N-1}$

$A_1$

$A_3$

$A_5$

$A_7$

…

…

$S ^ {N-2}$

$B_1 = \ гидроразрыва {A_1A_2-a_3a_0} {a_1}$

$B_2 = \ гидроразрыва {a_1a_4-a_5a_0} {a_1}$

$B_3 = \ гидроразрыва {a_1a_6-a_7a_0} {a_1}$

…

…

…

$S ^ {п-3}$

$C_1 = \ гидроразрыва {b_1a_3-b_2a_1} {b_1}$

$C_2 = \ гидроразрыва {b_1a_55-b_3a_1} {b_1}$

$\ Vdots$

$\ vdots$

$\ Vdots$

$\ Vdots$

$\ Vdots$

$S ^ 1$

$\ Vdots$

$\ Vdots$

$S ^ 0$

$A_n$

пример

Найдем устойчивость системы управления, имеющей характеристическое уравнение,

$$s ^ 4 + 3s ^ 3 + 3s ^ 2 + 2s + 1 = 0$$

Шаг 1 — Проверьте необходимое условие устойчивости Рауса-Гурвица.

Все коэффициенты характеристического полинома $s ^ 4 + 3s ^ 3 + 3s ^ 2 + 2s + 1$ положительны. Итак, система управления удовлетворяет необходимому условию.

Шаг 2 — Формируем массив Рауса для заданного характеристического полинома.

$S ^ 4$	$1$	$3$	$1$
$S ^ 3$	$3$	$2$
$S ^ 2$	$\ frac {(3 \ times 3) - (2 \ times 1)} {3} = \ frac {7} {3}$	$\ frac {(3 \ times 1) - (0 \ times 1)} {3} = \ frac {3} {3} = 1$
$S ^ 1$	$\ frac {\ left (\ frac {7} {3} \ times 2 \ right) - (1 \ times 3)} {\ frac {7} {3}} = \ frac {5} {7}$
$S ^ 0$	$1$

$S ^ 4$

$1$

$3$

$1$

$S ^ 3$

$3$

$2$

$S ^ 2$

$\ frac {(3 \ times 3) - (2 \ times 1)} {3} = \ frac {7} {3}$

$\ frac {(3 \ times 1) - (0 \ times 1)} {3} = \ frac {3} {3} = 1$

$S ^ 1$

$\ frac {\ left (\ frac {7} {3} \ times 2 \ right) - (1 \ times 3)} {\ frac {7} {3}} = \ frac {5} {7}$

$S ^ 0$

$1$

Шаг 3 — Проверьте достаточное условие устойчивости Рауса-Гурвица.

Все элементы первого столбца массива Рауса положительны. В первом столбце массива Routh нет изменения знака. Итак, система управления стабильна.

Особые случаи Routh Array

При формировании таблицы Рауса мы можем столкнуться с двумя типами ситуаций. Трудно заполнить таблицу Рауса из этих двух ситуаций.

Два особых случая:

• Первый элемент любой строки массива Routh равен нулю.
• Все элементы любой строки массива Routh равны нулю.

Давайте теперь обсудим, как преодолеть трудности в этих двух случаях, один за другим.

Первый элемент любой строки массива Routh равен нулю

Если какая-либо строка массива Routh содержит только первый элемент в качестве нуля и хотя бы один из оставшихся элементов имеет ненулевое значение, то замените первый элемент небольшим положительным целым числом, $\ epsilon$. А затем продолжите процесс заполнения таблицы Рауса. Теперь найдите число изменений знака в первом столбце таблицы Routh, подставив $\ epsilon$ в ноль.

пример

Найдем устойчивость системы управления, имеющей характеристическое уравнение,

$$s ^ 4 + 2s ^ 3 + з ^ 2 + 2s + 1 = 0$$

Шаг 1 — Проверьте необходимое условие устойчивости Рауса-Гурвица.

Все коэффициенты характеристического полинома $s ^ 4 + 2s ^ 3 + s ^ 2 + 2s + 1$ положительны. Итак, система управления удовлетворена необходимым условием.

Шаг 2 — Формируем массив Рауса для заданного характеристического полинома.

$S ^ 4$	$1$	$1$	$1$
$S ^ 3$	2 1	2 1
$S ^ 2$	$\ frac {(1 \ times 1) - (1 \ times 1)} {1} = 0$	$\ frac {(1 \ times 1) - (0 \ times 1)} {1} = 1$
$S ^ 1$
$S ^ 0$

$S ^ 4$

$1$

$1$

$1$

$S ^ 3$

2 1

2 1

$S ^ 2$

$\ frac {(1 \ times 1) - (1 \ times 1)} {1} = 0$

$\ frac {(1 \ times 1) - (0 \ times 1)} {1} = 1$

$S ^ 1$

$S ^ 0$

Элементы строки $s ^ 3$ имеют 2 в качестве общего множителя. Итак, все эти элементы делятся на 2.

Особый случай (i) — только первый элемент строки $s ^ 2$ равен нулю. Итак, замените его на $\ epsilon$ и продолжите процесс заполнения таблицы Рауса.

$S ^ 4$	1	1	1
$S ^ 3$	1	1
$S ^ 2$	$\ Эпсилон$	1
$S ^ 1$	$\ frac {\ left (\ epsilon \ times 1 \ right) - \ left (1 \ times 1 \ right)} {\ epsilon} = \ frac {\ epsilon-1} {\ epsilon}$
$S ^ 0$	1

$S ^ 4$

1

1

1

$S ^ 3$

1

1

$S ^ 2$

$\ Эпсилон$

1

$S ^ 1$

$\ frac {\ left (\ epsilon \ times 1 \ right) - \ left (1 \ times 1 \ right)} {\ epsilon} = \ frac {\ epsilon-1} {\ epsilon}$

$S ^ 0$

1

Шаг 3 — Проверьте достаточное условие устойчивости Рауса-Гурвица.

Когда $\ epsilon$ стремится к нулю, таблица Routh становится такой.

$S ^ 4$	1	1	1
$S ^ 3$	1	1
$S ^ 2$	0	1
$S ^ 1$	-∞
$S ^ 0$	1

$S ^ 4$

1

1

1

$S ^ 3$

1

1

$S ^ 2$

0

1

$S ^ 1$

-∞

$S ^ 0$

1

В первом столбце Routh таблицы есть два изменения знака. Следовательно, система управления нестабильна.

Все элементы любой строки массива Routh равны нулю

В этом случае выполните следующие два шага —

• Напишите вспомогательное уравнение A (s) строки, которая находится чуть выше ряда нулей.

• Дифференцируйте вспомогательное уравнение A (s) по s. Заполните ряд нулей этими коэффициентами.

Напишите вспомогательное уравнение A (s) строки, которая находится чуть выше ряда нулей.

Дифференцируйте вспомогательное уравнение A (s) по s. Заполните ряд нулей этими коэффициентами.

пример

Найдем устойчивость системы управления, имеющей характеристическое уравнение,

$$s ^ 5 + 3s ^ 4 + S ^ 3 + 3s ^ 2 + S + 3 = 0$$

Шаг 1 — Проверьте необходимое условие устойчивости Рауса-Гурвица.

Все коэффициенты данного характеристического полинома положительны. Итак, система управления удовлетворена необходимым условием.

Шаг 2 — Формируем массив Рауса для заданного характеристического полинома.

$S ^ 5$	1	1	1
$S ^ 4$	3 1	3 1	3 1
$S ^ 3$	$\ frac {(1 \ times 1) - (1 \ times 1)} {1} = 0$	$\ frac {(1 \ times 1) - (1 \ times 1)} {1} = 0$
$S ^ 2$
$S ^ 1$
$S ^ 0$

$S ^ 5$

1

1

1

$S ^ 4$

3 1

3 1

3 1

$S ^ 3$

$\ frac {(1 \ times 1) - (1 \ times 1)} {1} = 0$

$\ frac {(1 \ times 1) - (1 \ times 1)} {1} = 0$

$S ^ 2$

$S ^ 1$

$S ^ 0$

Элементы строки $s ^ 4$ имеют общий множитель 3. Итак, все эти элементы делятся на 3.

Особый случай (ii). Все элементы строки $s ^ 3$ равны нулю. Итак, запишите вспомогательное уравнение A (s) строки $s ^ 4$.

$$A (S) = S ^ 4 + з ^ 2 + 1$$

Дифференцируйте вышеприведенное уравнение по s.

$$\ гидроразрыва {\ текст {d} А (з)} {\ текст {d}} s = 4с ^ 3 + 2s$$

Поместите эти коэффициенты в строку $s ^ 3$.

$S ^ 5$	1	1	1
$S ^ 4$	1	1	1
$S ^ 3$	4 2	2 1
$S ^ 2$	$\ frac {(2 \ times 1) - (1 \ times 1)} {2} = 0,5$	$\ frac {(2 \ times 1) - (0 \ times 1)} {2} = 1$
$S ^ 1$	$\ frac {(0.5 \ times 1) - (1 \ times 2)} {0.5} = \ frac {-1.5} {0.5} = - 3$
$S ^ 0$	1

$S ^ 5$

1

1

1

$S ^ 4$

1

1

1

$S ^ 3$

4 2

2 1

$S ^ 2$

$\ frac {(2 \ times 1) - (1 \ times 1)} {2} = 0,5$

$\ frac {(2 \ times 1) - (0 \ times 1)} {2} = 1$

$S ^ 1$

$\ frac {(0.5 \ times 1) - (1 \ times 2)} {0.5} = \ frac {-1.5} {0.5} = - 3$

$S ^ 0$

1

Шаг 3 — Проверьте достаточное условие устойчивости Рауса-Гурвица.

В первом столбце Routh таблицы есть два изменения знака. Следовательно, система управления нестабильна.

В критерии устойчивости Рауса-Гурвица мы можем знать, находятся ли полюсы замкнутого контура в левой половине плоскости ‘s’ или в правой половине плоскости ‘s’ или на мнимой оси. Итак, мы не можем найти природу системы управления. Чтобы преодолеть это ограничение, существует метод, известный как корневой локус. Мы обсудим эту технику в следующих двух главах.

Системы управления — Root Locus

На диаграмме корневого локуса мы можем наблюдать путь полюсов замкнутого контура. Следовательно, мы можем определить природу системы управления. В этом методе мы будем использовать передаточную функцию с разомкнутым контуром, чтобы узнать стабильность системы управления с замкнутым контуром.

Основы корневого локуса

Корневой локус — это локус корней характеристического уравнения путем изменения коэффициента усиления системы K от нуля до бесконечности.

Мы знаем, что характеристическое уравнение замкнутой системы управления

$$1 + G (s) H (s) = 0$$

Мы можем представить $G (s) H (s)$ как

$$G (s) H (s) = K \ гидроразрыва {N (S)} {D (s)}$$

Куда,

• K представляет множитель

• N (s) представляет собой числитель, имеющий (факторированный) полином n- ^го порядка от ‘s’.

• D (s) представляет знаменатель, имеющий (факторированный) полином m- ^го порядка от ‘s’.

K представляет множитель

N (s) представляет собой числитель, имеющий (факторированный) полином n- ^го порядка от ‘s’.

D (s) представляет знаменатель, имеющий (факторированный) полином m- ^го порядка от ‘s’.

Подставим значение $G (s) H (s)$ в характеристическое уравнение.

$$1 + к \ гидроразрыва {N (S)} {D (s)} = 0$$

$$\ Rightarrow D (s) + KN (s) = 0$$

Случай 1 — К = 0

Если $K = 0$, то $D (s) = 0$.

Это означает, что полюса замкнутого контура равны полюсам разомкнутого контура, когда K равно нулю.

Случай 2 — K = ∞

Переписать приведенное выше характеристическое уравнение как

$$K \ left (\ frac {1} {K} + \ frac {N (s)} {D (s)} \ right) = 0 \ Rightarrow \ frac {1} {K} + \ frac {N ( с)} {D (s)} = 0$$

Замените $K = \ infty$ в приведенном выше уравнении.

$$\ frac {1} {\ infty} + \ frac {N (s)} {D (s)} = 0 \ Rightarrow \ frac {N (s)} {D (s)} = 0 \ Rightarrow N ( з) = 0$$

Если $K = \ infty$, то $N (s) = 0$. Это означает, что полюса замкнутого контура равны нулям разомкнутого контура, когда K бесконечность.

Из приведенных выше двух случаев можно сделать вывод, что ветви корневого локуса начинаются с полюсов разомкнутого контура и заканчиваются в нулях разомкнутого контура.

Угловое состояние и условие величины

Точки на ветвях корневого локуса удовлетворяют условию угла. Таким образом, условие угла используется, чтобы узнать, существует ли точка на ветви корневого локуса или нет. Мы можем найти значение K для точек на ветвях корневого локуса, используя условие величины. Таким образом, мы можем использовать условие величины для точек, и это удовлетворяет условию угла.

Характеристическое уравнение замкнутой системы управления

$$1 + G (s) H (s) = 0$$

$$\ Rightarrow G (s) H (s) = - 1 + j0$$

Фазовый угол $G (s) H (s)$ равен

$$\ angle G (s) H (s) = \ tan ^ {- 1} \ left (\ frac {0} {- 1} \ right) = (2n + 1) \ pi$$

Условие угла — это точка, в которой угол передаточной функции разомкнутого контура нечетно кратен 180 ⁰ .

Величина $G (s) H (s)$ составляет —

$$| G (s) H (s) | = \ sqrt {(-1) ^ 2 + 0 ^ 2} = 1$$

Условием величины является то, что точка (которая удовлетворяла условию угла), в которой величина передаточной функции разомкнутого контура равна единице.

Строительство корневого локуса

Корневой локус является графическим представлением в s-области, и он симметричен относительно действительной оси. Потому что полюсы и нули в разомкнутом контуре существуют в s-области, имеющей значения в виде вещественных или комплексных сопряженных пар. В этой главе давайте обсудим, как построить (нарисовать) корневой локус.

Правила построения корневого локуса

Следуйте этим правилам для построения корневого локуса.

Правило 1 — Найдите полюсы и нули разомкнутой петли в плоскости ‘s’.

Правило 2 — Найти количество ветвей корневых локусов.

Мы знаем, что ветви корневых локусов начинаются на полюсах разомкнутого контура и заканчиваются на нулях разомкнутого контура. Таким образом, число ветвей корневых локусов N равно числу конечных полюсов разомкнутой петли P или числу конечных нулей разомкнутой петли Z , в зависимости от того, что больше.

Математически мы можем записать число корневых ветвей локуса N как

$N = P$, если $P \ geq Z$

$N = Z$, если $P &amp;lt;Z$

Правило 3 — Определите и нарисуйте ветви корневых локусов реальной оси .

Если угол передаточной функции разомкнутого контура в точке нечетно кратен 180 ⁰ , то эта точка находится в корневом локусе. Если нечетное число полюсов и нулей разомкнутой петли существует слева от точки на действительной оси, то эта точка находится на ветви корневого локуса. Следовательно, ветвь точек, которая удовлетворяет этому условию, является действительной осью ветви корневого локуса.

Правило 4 — Найдите центроид и угол асимптоты.

• Если $P = Z$, то все ветви корневых локусов начинаются с конечных полюсов разомкнутой петли и заканчиваются конечными нулями разомкнутой петли.

• Если $P&amp;gt; Z$, то число корневых локусных ветвей $Z$ начинается с конечных полюсов разомкнутой петли и заканчивается в нулях конечной разомкнутой петли, а число корневых локусных ветвей $P - Z$ начинается с конечных полюсов разомкнутой петли и заканчивается на бесконечных нули с разомкнутым контуром.

• Если $P &amp;lt;Z$, то число корневых локусных ветвей P начинается с конечных полюсов разомкнутой петли и заканчивается на конечных нулях разомкнутой петли, а число Z — P $ корневых ветвей локуса начинается с бесконечных полюсов разомкнутой петли и заканчивается в конечной разомкнутой петле нули.

Если $P = Z$, то все ветви корневых локусов начинаются с конечных полюсов разомкнутой петли и заканчиваются конечными нулями разомкнутой петли.

Если $P&amp;gt; Z$, то число корневых локусных ветвей $Z$ начинается с конечных полюсов разомкнутой петли и заканчивается в нулях конечной разомкнутой петли, а число корневых локусных ветвей $P - Z$ начинается с конечных полюсов разомкнутой петли и заканчивается на бесконечных нули с разомкнутым контуром.

Если $P &amp;lt;Z$, то число корневых локусных ветвей P начинается с конечных полюсов разомкнутой петли и заканчивается на конечных нулях разомкнутой петли, а число Z — P $ корневых ветвей локуса начинается с бесконечных полюсов разомкнутой петли и заканчивается в конечной разомкнутой петле нули.

Итак, некоторые ветви корневых локусов приближаются к бесконечности, когда $P \ neq Z$. Асимптоты указывают направление ветвей корневых локусов. Точка пересечения асимптот на реальной оси называется центроидом .

Мы можем рассчитать центроид α , используя эту формулу,

$\ alpha = \ frac {\ sum Real \: part \: of \: конечный \: open \: loop \: poles \: - \ sum Real \: part \: of \: of \: конечный \: open \: loop \ : нули} {PZ}$

Формула для угла асимптот θ имеет вид

$$\ тета = \ гидроразрыва {(2q + 1), 180 ^ 0} {PZ}$$

Куда,

$$д = 0,1,2, ...., (ПЗ) -1$$

Правило 5 — Найдите точки пересечения ветвей корневых локусов с мнимой осью.

Мы можем вычислить точку, в которой корневая ветвь локуса пересекает мнимую ось и значение K в этой точке, используя метод массива Рауса и специальный случай (ii) .

• Если все элементы какой-либо строки массива Рауса равны нулю, тогда корневая ветвь локуса пересекает мнимую ось и наоборот.

• Определите строку таким образом, что если мы сделаем первый элемент нулевым, то элементы всей строки будут равны нулю. Найдите значение K для этой комбинации.

• Подставьте это значение K во вспомогательное уравнение. Вы получите точку пересечения ветви корневого локуса с мнимой осью.

Если все элементы какой-либо строки массива Рауса равны нулю, тогда корневая ветвь локуса пересекает мнимую ось и наоборот.

Определите строку таким образом, что если мы сделаем первый элемент нулевым, то элементы всей строки будут равны нулю. Найдите значение K для этой комбинации.

Подставьте это значение K во вспомогательное уравнение. Вы получите точку пересечения ветви корневого локуса с мнимой осью.

Правило 6 — Найти точки отрыва и взлома.

• Если между двумя полюсами разомкнутого контура существует ветвь корневого локуса реальной оси, то между этими двумя полюсами разомкнутого контура будет точка отрыва .

• Если между двумя нулями разомкнутого контура существует ветвь корневого локуса действительной оси, то между этими двумя нулями разомкнутого контура будет точка разрыва .

Если между двумя полюсами разомкнутого контура существует ветвь корневого локуса реальной оси, то между этими двумя полюсами разомкнутого контура будет точка отрыва .

Если между двумя нулями разомкнутого контура существует ветвь корневого локуса действительной оси, то между этими двумя нулями разомкнутого контура будет точка разрыва .

Примечание. Точки отрыва и взлома существуют только на ветвях корневых локусов реальной оси.

Выполните следующие действия, чтобы найти точки отрыва и взлома.

• Запишите $K$ в терминах $s$ из характеристического уравнения $1 + G (s) H (s) = 0$.

• Продифференцируйте $K$ по s и сделайте его равным нулю. Подставьте эти значения $s$ в приведенном выше уравнении.

• Значения $s$, для которых значение $K$ является положительным, являются точками разрыва .

Запишите $K$ в терминах $s$ из характеристического уравнения $1 + G (s) H (s) = 0$.

Продифференцируйте $K$ по s и сделайте его равным нулю. Подставьте эти значения $s$ в приведенном выше уравнении.

Значения $s$, для которых значение $K$ является положительным, являются точками разрыва .

Правило 7 — Найдите угол вылета и угол прибытия.

Угол вылета и угол прихода могут быть рассчитаны для комплексных сопряженных полюсов разомкнутой петли и комплексных сопряженных нулей разомкнутой петли соответственно.

Формула для угла вылета $\ phi_d$:

$$\ phi_d = 180 ^ 0- \ Phi$$

Формула для угла прихода $\ phi_a$:

$$\ phi_a = 180 ^ 0 + \ Phi$$

Куда,

$$\ phi = \ sum \ phi_P- \ sum \ phi_Z$$

пример

Теперь нарисуем корневой локус системы управления, имеющей передаточную функцию с разомкнутым контуром, $G (s) H (s) = \ frac {K} {s (s + 1) (s + 5)}$

Шаг 1 — Данная передаточная функция с разомкнутым контуром имеет три полюса при $s = 0, s = −1$ и $s = −5$. У него нет нуля. Следовательно, число ветвей корневых локусов равно числу полюсов передаточной функции разомкнутого контура.

$$N = Р = 3$$

Три полюса расположены, как показано на рисунке выше. Сегмент прямой между $s = −1$ и $s = 0$ является одной ветвью корневого локуса на действительной оси. А другая ветвь корневого локуса на действительной оси — это отрезок слева от $s = −5$.

Шаг 2 — Мы получим значения центроида и угла асимптоты, используя данные формулы.

Центроид $\ alpha = −2$

Угол асимптоты составляет $\ theta = 60 ^ 0,180 ^ 0$ и $300 ^ 0$.

Центроид и три асимптоты показаны на следующем рисунке.

Шаг 3 — Поскольку две асимптоты имеют углы $60 ^ 0$ и $300 ^ 0$, две ветви корневых локусов пересекают мнимую ось. Используя метод массива Рауса и особый случай (ii), ветви корневых локусов пересекают мнимую ось в $j \ sqrt {5}$ и $−j \ sqrt {5}$.

Будет одна точка отрыва на ветви корневого локуса реальной оси между полюсами $s = −1$ и $s = 0$. Следуя процедуре, данной для расчета точки отрыва, мы получим ее как $s = −0,473$.

Диаграмма корневого локуса для данной системы управления показана на следующем рисунке.

Таким образом, вы можете нарисовать диаграмму корневого локуса любой системы управления и наблюдать за перемещением полюсов передаточной функции замкнутого контура.

Из диаграмм корневых локусов мы можем узнать диапазон значений K для различных типов демпфирования.

Эффекты добавления полюсов и нулей с открытой петлей на корневой локус

Корневой локус может быть сдвинут в плоскости ‘s’ путем добавления полюсов разомкнутого контура и нулей разомкнутого контура.

• Если мы включим полюс в передаточную функцию разомкнутого контура, то некоторые ветви корневого локуса будут двигаться к правой половине плоскости ‘s’. Из-за этого коэффициент демпфирования $\ delta$ уменьшается. Это означает, что демпфированная частота $\ omega_d$ увеличивается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, уменьшаются. Но это влияет на стабильность системы.

• Если мы включим ноль в передаточную функцию разомкнутого контура, то некоторые ветви корневых локусов переместятся к левой половине плоскости ‘s’. Таким образом, это повысит стабильность системы управления. В этом случае коэффициент демпфирования $\ delta$ увеличивается. Это означает, что демпфированная частота $\ omega_d$ уменьшается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, увеличиваются.

Если мы включим полюс в передаточную функцию разомкнутого контура, то некоторые ветви корневого локуса будут двигаться к правой половине плоскости ‘s’. Из-за этого коэффициент демпфирования $\ delta$ уменьшается. Это означает, что демпфированная частота $\ omega_d$ увеличивается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, уменьшаются. Но это влияет на стабильность системы.

Если мы включим ноль в передаточную функцию разомкнутого контура, то некоторые ветви корневых локусов переместятся к левой половине плоскости ‘s’. Таким образом, это повысит стабильность системы управления. В этом случае коэффициент демпфирования $\ delta$ увеличивается. Это означает, что демпфированная частота $\ omega_d$ уменьшается, а спецификации временной области, такие как время задержки $t_d$, время нарастания $t_r$ и время пика $t_p$, увеличиваются.

Таким образом, основываясь на требовании, мы можем включить (добавить) полюсы или нули разомкнутого контура в передаточную функцию.

Анализ частотных характеристик

Мы уже обсуждали анализ времени отклика систем управления и спецификации временной области систем управления второго порядка. В этой главе мы обсудим анализ частотных характеристик систем управления и спецификации частотной области систем управления второго порядка.

Что такое частотный отклик?

Реакция системы может быть разделена как на переходную реакцию, так и на реакцию в установившемся режиме. Мы можем найти переходный отклик, используя интегралы Фурье. Отклик установившегося состояния системы на входной синусоидальный сигнал известен как частотный отклик . В этой главе мы сосредоточимся только на реакции устойчивого состояния.

Если синусоидальный сигнал подается в качестве входа в систему с линейной инвариантностью во времени (LTI), то он вырабатывает выход в устойчивом состоянии, который также является синусоидальным сигналом. Входные и выходные синусоидальные сигналы имеют одинаковую частоту, но разные амплитуды и фазовые углы.

Пусть входной сигнал будет —

$$R (T) = A \ sin (\ omega_0t)$$

Передаточная функция с разомкнутым контуром будет —

$$G (s) = G (J \ омега)$$

Мы можем представить $G (j \ omega)$ в терминах величины и фазы, как показано ниже.

$$ G (J \ омега) = | G (J \ омега) | \ angle G (j \ omega) $$

Замените $\ omega = \ omega_0$ в приведенном выше уравнении.

$$ G (J \ omega_0) = | G (J \ omega_0) | \ angle G (j \ omega_0) $$

Выходной сигнал

$$c (t) = A | G (j \ omega_0) | \ sin (\ omega_0t + \ angle G (j \ omega_0))$$

• Амплитуда выходного синусоидального сигнала получается путем умножения амплитуды входного синусоидального сигнала и величины $G (j \ omega)$ на $\ omega = \ omega_0$.

• Фаза выходного синусоидального сигнала получается путем сложения фазы входного синусоидального сигнала и фазы $G (j \ omega)$ при $\ omega = \ omega_0$.

Амплитуда выходного синусоидального сигнала получается путем умножения амплитуды входного синусоидального сигнала и величины $G (j \ omega)$ на $\ omega = \ omega_0$.

Фаза выходного синусоидального сигнала получается путем сложения фазы входного синусоидального сигнала и фазы $G (j \ omega)$ при $\ omega = \ omega_0$.

Куда,

• А — амплитуда входного синусоидального сигнала.

• ω ₀ — угловая частота входного синусоидального сигнала.

А — амплитуда входного синусоидального сигнала.

ω ₀ — угловая частота входного синусоидального сигнала.

Мы можем написать угловую частоту $\ omega_0$, как показано ниже.

$$\ omega_0 = 2 \ pi f_0$$

Здесь $f_0$ — частота входного синусоидального сигнала. Точно так же вы можете следовать той же процедуре для замкнутой системы управления.

Спецификации частотной области

Спецификации частотной области: резонансный пик, резонансная частота и ширина полосы .

Рассмотрим передаточную функцию замкнутой системы управления второго порядка как,

$$T (S) = \ гидроразрыва {C (S)} {R (S)} = \ {гидроразрыва \ omega_n ^ 2} {s ^ 2 + 2 \ дельта \ omega_ns + \ omega_n ^ 2}$$

Замените $s = j \ omega$ в приведенном выше уравнении.

$$T (J \ Omega) = \ гидроразрыва {\ omega_n ^ 2} {(J \ Omega) ^ 2 + 2 \ дельта \ omega_n (J \ Omega) + \ omega_n ^ 2}$$

$$\ Rightarrow T (j \ omega) = \ frac {\ omega_n ^ 2} {- \ omega ^ 2 + 2j \ delta \ omega \ omega_n + \ omega_n ^ 2} = \ frac {\ omega_n ^ 2} {\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)}$$

$$\ Rightarrow T (j \ omega) = \ frac {1} {\ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} \ right) + j \ left (\ frac {2 \ delta \ omega} {\ omega_n} \ right)}$$

Пусть $\ frac {\ omega} {\ omega_n} = u$ Подставим это значение в вышеприведенное уравнение.

$$T (j \ omega) = \ frac {1} {(1-u ^ 2) + j (2 \ delta u)}$$

Величина $T (j \ omega)$ равна —

$$M = | T (j \ omega) | = \ frac {1} {\ sqrt {(1-u ^ 2) ^ 2 + (2 \ delta u) ^ 2}}$$

Фаза $T (j \ omega)$ — это

$$\ angle T (j \ omega) = - tan ^ {- 1} \ left (\ frac {2 \ delta u} {1-u ^ 2} \ right)$$

Резонансная частота

Это частота, на которой величина частотной характеристики впервые имеет пиковое значение. Обозначается $\ omega_r$. При $\ omega = \ omega_r$ первый производный величины $T (j \ omega)$ равен нулю.

Продифференцируйте $M$ относительно $u$.

$$\ frac {\ text {d} M} {\ text {d} u} = - \ frac {1} {2} \ left [(1-u ^ 2) ^ 2 + (2 \ delta u) ^ 2 \ right] ^ {\ frac {-3} {2}} \ left [2 (1-u ^ 2) (- 2u) +2 (2 \ delta u) (2 \ delta) \ right]$$

$$\ Rightarrow \ frac {\ text {d} M} {\ text {d} u} = - \ frac {1} {2} \ left [(1-u ^ 2) ^ 2 + (2 \ delta u ) ^ 2 \ right] ^ {\ frac {-3} {2}} \ left [4u (u ^ 2-1 +2 \ delta ^ 2) \ right]$$

Замените $u = u_r$ и $\ frac {\ text {d} M} {\ text {d} u} == 0$ в вышеприведенном уравнении.

$$0 = - \ frac {1} {2} \ left [(1-u_r ^ 2) ^ 2 + (2 \ delta u_r) ^ 2 \ right] ^ {- \ frac {3} {2}} \ left [4u_r (u_r ^ 2-1 +2 \ delta ^ 2) \ right]$$

$$\ Rightarrow 4u_r (u_r ^ 2-1 +2 \ delta ^ 2) = 0$$

$$\ Rightarrow u_r ^ 2-1 + 2 \ delta ^ 2 = 0$$

$$\ Rightarrow u_r ^ 2 = 1-2 \ delta ^ 2$$

$$\ Rightarrow u_r = \ sqrt {1-2 \ delta ^ 2}$$

Замените $u_r = \ frac {\ omega_r} {\ omega_n}$ в приведенном выше уравнении.

$$\ гидроразрыва {\ omega_r} {\ omega_n} = \ SQRT {1-2 \ Delta ^ 2}$$

$$\ Rightarrow \ omega_r = \ omega_n \ sqrt {1-2 \ delta ^ 2}$$

Резонансный пик

Это пиковое (максимальное) значение величины $T (j \ omega)$. Обозначается $M_r$.

При $u = u_r$ величина $T (j \ omega)$ равна —

$$M_r = \ frac {1} {\ sqrt {(1-u_r ^ 2) ^ 2 + (2 \ delta u_r) ^ 2}}$$

Замените $u_r = \ sqrt {1 - 2 \ delta ^ 2}$ и $1 - u_r ^ 2 = 2 \ delta ^ 2$ в вышеприведенном уравнении.

$$M_r = \ frac {1} {\ sqrt {(2 \ delta ^ 2) ^ 2 + (2 \ delta \ sqrt {1-2 \ delta ^ 2}) ^ 2}}$$

$$\ Rightarrow M_r = \ frac {1} {2 \ delta \ sqrt {1- \ delta ^ 2}}$$

Резонансный пик в частотной характеристике соответствует пиковому превышению в переходной характеристике во временной области для определенных значений коэффициента затухания $\ delta$. Таким образом, резонансный пик и выброс пика коррелируют друг с другом.

Пропускная способность

Это диапазон частот, в котором величина $T (j \ omega)$ падает до 70,7% от нулевого значения частоты.

При $\ omega = 0$ значение $u$ будет равно нулю.

Подставим $u = 0$ в M.

$$M = \ frac {1} {\ sqrt {(1-0 ^ 2) ^ 2 + (2 \ delta (0)) ^ 2}} = 1$$

Следовательно, величина $T (j \ omega)$ равна единице при $\ omega = 0$.

При частоте 3 дБ величина $T (j \ omega)$ будет составлять 70,7% от величины $T (j \ omega)$ при $\ omega = 0$.

т. е. при $\ omega = \ omega_B, M = 0,707 (1) = \ frac {1} {\ sqrt {2}}$

$$\ Rightarrow M = \ frac {1} {\ sqrt {2}} = \ frac {1} {\ sqrt {(1-u_b ^ 2) ^ 2 + (2 \ delta u_b) ^ 2}}$$

$$\ Rightarrow 2 = (1-u_b ^ 2) ^ 2 + (2 \ delta) ^ 2 u_b ^ 2$$

Пусть, $u_b ^ 2 = x$

$$\ Rightarrow 2 = (1-x) ^ 2 + (2 \ delta) ^ 2 x$$

$$\ Rightarrow x ^ 2 + (4 \ delta ^ 2-2) x-1 = 0$$

$$\ Rightarrow x = \ frac {- (4 \ delta ^ 2 -2) \ pm \ sqrt {(4 \ delta ^ 2-2) ^ 2 + 4}} {2}$$

Рассмотрим только положительное значение х.

$$x = 1-2 \ delta ^ 2 + \ sqrt {(2 \ delta ^ 2-1) ^ 2 + 1}$$

$$\ Rightarrow x = 1-2 \ delta ^ 2 + \ sqrt {(2-4 \ delta ^ 2 + 4 \ delta ^ 4)}$$

Заменить $x = u_b ^ 2 = \ frac {\ omega_b ^ 2} {\ omega_n ^ 2}$

$$\ frac {\ omega_b ^ 2} {\ omega_n ^ 2} = 1-2 \ delta ^ 2 + \ sqrt {(2-4 \ delta ^ 2 + 4 \ delta ^ 4)}$$

$$\ Rightarrow \ omega_b = \ omega_n \ sqrt {1-2 \ delta ^ 2 + \ sqrt {(2-4 \ delta ^ 2 + 4 \ delta ^ 4)}}$$

Полоса пропускания $\ omega_b$ в частотной характеристике обратно пропорциональна времени нарастания $t_r$ в переходной характеристике во временной области.

Системы управления — участки Боде

Сюжет Боде или диаграмма Боде состоит из двух участков —

• Величина участка
• Фазовый сюжет

На обоих графиках ось X представляет угловую частоту (логарифмическая шкала). Принимая во внимание, что yaxis представляет величину (линейный масштаб) передаточной функции разомкнутого контура на графике амплитуды и фазовый угол (линейный масштаб) передаточной функции разомкнутого контура на фазовом графике.

Величина передаточной функции разомкнутого контура в дБ составляет —

$$M = 20 \: \ log | G (j \ omega) H (j \ omega) |$$

Фазовый угол передаточной функции разомкнутого контура в градусах —

$$\ phi = \ angle G (j \ omega) H (j \ omega)$$

Примечание . Основание логарифма — 10.

Базовые участки Боде

В следующей таблице приведены значения наклона, величины и фазового угла членов, присутствующих в передаточной функции разомкнутого контура. Эти данные полезны при рисовании графиков Боде.

Тип термина	G (jω) Н (jω)	Наклон (дБ / декабрь)	Величина (дБ)	Фазовый угол (градусы)
постоянная	$K$	$0$	$20 \ log K$	$0$
Ноль в начале	$J \ Omega$	$20$	$20 \ log \ omega$	$90$
нули в начале координат	$(К \ омега) ^ п$	$20 \: n$	$20 \: n \ log \ omega$	$90 \: n$
Полюс в начале координат	$\ Гидроразрыва {1} {J \ Omega}$	$-20$	$-20 \ log \ omega$	$-90 \: или \: 270$
полюса ‘n’ в начале координат	$\ Гидроразрыв {1} {(к \ омега) ^ п}$	$-20 \: n$	$-20 \: n \ log \ omega$	$-90 \: n \: или \: 270 \: n$
Простой ноль	$1 + j \ omega r$	$20$	$0 \: for \: \ omega <\ frac {1} {r}$ $20 \: \ log \ omega r \: for \: \ omega> \ frac {1} {r}$	$0 \: for \: \ omega <\ frac {1} {r}$ $90 \: for \: \ omega> \ frac {1} {r}$
Простой полюс	$\ frac {1} {1 + j \ omega r}$	$-20$	$0 \: for \: \ omega <\ frac {1} {r}$ $-20 \: \ log \ omega r \: for \: \ omega> \ frac {1} {r}$	$0 \: for \: \ omega <\ frac {1} {r}$ $-90 \: или \: 270 \: для \: \ omega> \ frac {1} {r}$
Производный член второго порядка	$\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)$	$40$	$40 \: \ log \: \ omega_n \: for \: \ omega <\ omega_n$ $20 \: \ log \ 🙁 2 \ delta \ omega_n ^ 2) \: for \: \ omega = \ omega_n$ $40 \: \ log \: \ omega \: for \: \ omega> \ omega_n$	$0 \: для \: \ omega <\ omega_n$ $90 \: для \: \ omega = \ omega_n$ $180 \: для \: \ omega> \ omega_n$
Интегральный член второго порядка	$\ frac {1} {\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)}$	$-40$	$-40 \: \ log \: \ omega_n \: for \: \ omega <\ omega_n$ $-20 \: \ log \ 🙁 2 \ delta \ omega_n ^ 2) \: for \: \ omega = \ omega_n$ $-40 \: \ log \: \ omega \: for \: \ omega> \ omega_n$	$-0 \: for \: \ omega <\ omega_n$ $-90 \: для \: \ omega = \ omega_n$ $-180 \: для \: \ omega> \ omega_n$

постоянная

$K$

$0$

$20 \ log K$

$0$

Ноль в начале

$J \ Omega$

$20$

$20 \ log \ omega$

$90$

нули в начале координат

$(К \ омега) ^ п$

$20 \: n$

$20 \: n \ log \ omega$

$90 \: n$

Полюс в начале координат

$\ Гидроразрыва {1} {J \ Omega}$

$-20$

$-20 \ log \ omega$

$-90 \: или \: 270$

полюса ‘n’ в начале координат

$\ Гидроразрыв {1} {(к \ омега) ^ п}$

$-20 \: n$

$-20 \: n \ log \ omega$

$-90 \: n \: или \: 270 \: n$

Простой ноль

$1 + j \ omega r$

$20$

$0 \: for \: \ omega &amp;lt;\ frac {1} {r}$

$20 \: \ log \ omega r \: for \: \ omega&amp;gt; \ frac {1} {r}$

$0 \: for \: \ omega &amp;lt;\ frac {1} {r}$

$90 \: for \: \ omega&amp;gt; \ frac {1} {r}$

Простой полюс

$\ frac {1} {1 + j \ omega r}$

$-20$

$0 \: for \: \ omega &amp;lt;\ frac {1} {r}$

$-20 \: \ log \ omega r \: for \: \ omega&amp;gt; \ frac {1} {r}$

$0 \: for \: \ omega &amp;lt;\ frac {1} {r}$

$-90 \: или \: 270 \: для \: \ omega&amp;gt; \ frac {1} {r}$

Производный член второго порядка

$\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)$

$40$

$40 \: \ log \: \ omega_n \: for \: \ omega &amp;lt;\ omega_n$

$20 \: \ log \ 🙁 2 \ delta \ omega_n ^ 2) \: for \: \ omega = \ omega_n$

$40 \: \ log \: \ omega \: for \: \ omega&amp;gt; \ omega_n$

$0 \: для \: \ omega &amp;lt;\ omega_n$

$90 \: для \: \ omega = \ omega_n$

$180 \: для \: \ omega&amp;gt; \ omega_n$

Интегральный член второго порядка

$\ frac {1} {\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)}$

$-40$

$-40 \: \ log \: \ omega_n \: for \: \ omega &amp;lt;\ omega_n$

$-20 \: \ log \ 🙁 2 \ delta \ omega_n ^ 2) \: for \: \ omega = \ omega_n$

$-40 \: \ log \: \ omega \: for \: \ omega&amp;gt; \ omega_n$

$-0 \: for \: \ omega &amp;lt;\ omega_n$

$-90 \: для \: \ omega = \ omega_n$

$-180 \: для \: \ omega&amp;gt; \ omega_n$

Рассмотрим передаточную функцию с разомкнутым контуром $G (s) H (s) = K$.

Величина $M = 20 \: \ log K$ дБ

Фазовый угол $\ phi = 0$ градусов

Если $K = 1$, то величина равна 0 дБ.

Если $K&amp;gt; 1$, то величина будет положительной.

Если $K &amp;lt;1$, то величина будет отрицательной.

На следующем рисунке показан соответствующий участок Боде.

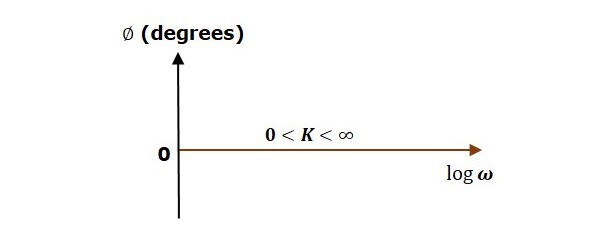
График величины представляет собой горизонтальную линию, которая не зависит от частоты. Сама линия 0 дБ представляет собой график величины, когда значение K равно единице. Для положительных значений K горизонтальная линия сместится на $20 \: \ log K$ дБ выше линии 0 дБ. Для отрицательных значений K горизонтальная линия сместится на $20 \: \ log K$ дБ ниже линии 0 дБ. Сама линия нулевых градусов является фазовым графиком для всех положительных значений K.

Рассмотрим передаточную функцию с разомкнутым контуром $G (s) H (s) = s$.

Величина $M = 20 \ log \ omega$ дБ

Фазовый угол $\ phi = 90 ^ 0$

При $\ omega = 0,1$ рад / с величина составляет -20 дБ.

При $\ omega = 1$ рад / с величина составляет 0 дБ.

При $\ omega = 10$ рад / с величина составляет 20 дБ.

На следующем рисунке показан соответствующий участок Боде.

График величины представляет собой линию, которая имеет наклон 20 дБ / дек. Эта линия начиналась со значения $\ omega = 0,1$ рад / с, имеющего величину -20 дБ, и продолжается на том же наклоне. Он касается линии 0 дБ при $\ omega = 1$ рад / с. В этом случае фазовый участок составляет 90 ⁰ линии.

Рассмотрим передаточную функцию с разомкнутым контуром $G (s) H (s) = 1 + s \ tau$.

Величина $M = 20 \: log \ sqrt {1 + \ omega ^ 2 \ tau ^ 2}$ дБ

Фазовый угол $\ phi = \ tan ^ {- 1} \ omega \ tau$ градусов

Для $ω &amp;lt;\ frac {1} {\ tau}$ величина равна 0 дБ, а фазовый угол равен 0 градусам.

Для $\ omega&amp;gt; \ frac {1} {\ tau}$ величина составляет $20 \: \ log \ omega \ tau$ dB, а фазовый угол равен 90 ⁰ .

На следующем рисунке показан соответствующий участок Боде.

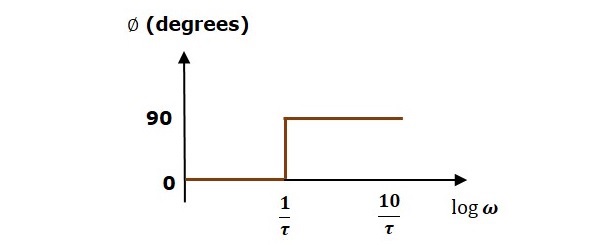
График величины имеет величину от 0 дБ до $\ omega = \ frac {1} {\ tau}$ рад / с. Из $\ omega = \ frac {1} {\ tau}$ рад / с он имеет наклон 20 дБ / дек. В этом случае фазовый график имеет фазовый угол от 0 градусов до $\ omega = \ frac {1} {\ tau}$ рад / с, и отсюда он имеет фазовый угол 90 ⁰ . Этот сюжет Боде называется асимптотическим сюжетом Боде .

Поскольку величины и фазовые диаграммы представлены прямыми линиями, точные графики Боде напоминают асимптотические графики Боде. Единственное отличие состоит в том, что графики Точного Боде будут иметь простые кривые вместо прямых.

Точно так же вы можете нарисовать графики Боде для других членов передаточной функции разомкнутого контура, которые приведены в таблице.

Системы управления — строительство участков Боде

В этой главе давайте подробно разберемся, как построить (нарисовать) графики Боде.

Правила застройки участков Боде

Следуйте этим правилам при построении сюжета Боде.

• Представьте передаточную функцию разомкнутого контура в стандартной форме постоянной времени.

• Замените $s = j \ omega$ в приведенном выше уравнении.

• Найдите угловые частоты и расположите их в порядке возрастания.

• Рассмотрим начальную частоту графика Боде как 1/10 от минимальной угловой частоты или 0,1 рад / с, в зависимости от того, какое значение меньше, и нарисуйте график Боде до 10-кратной максимальной угловой частоты.

• Нарисуйте графики величины для каждого слагаемого и правильно объедините эти графики.

• Нарисуйте фазовые графики для каждого термина и правильно объедините эти графики.

Представьте передаточную функцию разомкнутого контура в стандартной форме постоянной времени.

Замените $s = j \ omega$ в приведенном выше уравнении.

Найдите угловые частоты и расположите их в порядке возрастания.

Рассмотрим начальную частоту графика Боде как 1/10 от минимальной угловой частоты или 0,1 рад / с, в зависимости от того, какое значение меньше, и нарисуйте график Боде до 10-кратной максимальной угловой частоты.

Нарисуйте графики величины для каждого слагаемого и правильно объедините эти графики.

Нарисуйте фазовые графики для каждого термина и правильно объедините эти графики.

Примечание . Угловая частота — это частота, с которой происходит изменение наклона графика величины.

пример

Рассмотрим передаточную функцию без обратной связи системы управления с обратной связью

$$G (s) H (s) = \ гидроразрыва {10s} {(s + 2) (с + 5)}$$

Давайте преобразуем эту передаточную функцию с открытым контуром в стандартную форму постоянной времени.

$$G (s) H (s) = \ frac {10s} {2 \ left (\ frac {s} {2} +1 \ right) 5 \ left (\ frac {s} {5} +1 \ right )}$$

$$\ Rightarrow G (s) H (s) = \ frac {s} {\ left (1+ \ frac {s} {2} \ right) \ left (1+ \ frac {s} {5} \ right )}$$

Таким образом, мы можем нарисовать график Боде в полулоголотом, используя правила, упомянутые ранее.

Анализ устойчивости с использованием диаграмм Боде

Из графиков Боде мы можем сказать, является ли система управления стабильной, незначительно стабильной или нестабильной, основываясь на значениях этих параметров.

• Усиление частоты и частоты фазового перехода
• Прибыль маржи и фазовая маржа

Фаза пересечения частоты

Частота, на которой фазовый график имеет фазу -180 ^0, называется частотой пересечения фаз . Он обозначается как $\ omega_ {pc}$. Единица частоты фазового перехода равна рад / с .

Усиление пересекает частоту

Частота, на которой график амплитуды имеет величину ноль дБ, называется частотой перехода усиления . Он обозначается как $\ omega_ {gc}$. Единица усиления частоты перехода составляет рад / с .

Стабильность системы управления на основе соотношения между частотой перехода фазы и частотой перехода усиления приведена ниже.

• Если частота перехода фазы $\ omega_ {pc}$ больше частоты перехода коэффициента усиления $\ omega_ {gc}$, то система управления устойчива .

• Если частота перехода фазы $\ omega_ {pc}$ равна частоте перехода усиления $\ omega_ {gc}$, то система управления является минимально устойчивой .

• Если частота пересечения фазы $\ omega_ {pc}$ меньше частоты пересечения усиления $\ omega_ {gc}$, то система управления неустойчива .

Если частота перехода фазы $\ omega_ {pc}$ больше частоты перехода коэффициента усиления $\ omega_ {gc}$, то система управления устойчива .

Если частота перехода фазы $\ omega_ {pc}$ равна частоте перехода усиления $\ omega_ {gc}$, то система управления является минимально устойчивой .

Если частота пересечения фазы $\ omega_ {pc}$ меньше частоты пересечения усиления $\ omega_ {gc}$, то система управления неустойчива .

Получить маржу

Запас усиления $GM$ равен отрицательной величине в дБ при частоте пересечения фаз.

$$GM = 20 \ log \ left (\ frac {1} {M_ {pc}} \ right) = 20logM_ {pc}$$

Где $M_ {pc}$ — это величина на частоте перехода фазы. Единица усиления (GM) составляет дБ .

Фазовая маржа

Формула для фазовой маржи $PM$ имеет вид

$$PM = 180 ^ 0 + \ Phi_ {дс}$$

Где $\ phi_ {gc}$ — фазовый угол на частоте перехода усиления. Единица фазового поля — градусы .

Стабильность системы управления, основанная на связи между запасом усиления и запасом по фазе, указана ниже.

• Если и маржа усиления $GM$, и фазовая маржа $PM$ положительны, то система управления стабильна .

• Если и маржа усиления $GM$, и фазовая маржа $PM$ равны нулю, то система управления незначительно стабильна .

• Если запас усиления $GM$ и / или запас по фазе $PM$ являются / отрицательными, то система управления нестабильна .

Если и маржа усиления $GM$, и фазовая маржа $PM$ положительны, то система управления стабильна .

Если и маржа усиления $GM$, и фазовая маржа $PM$ равны нулю, то система управления незначительно стабильна .

Если запас усиления $GM$ и / или запас по фазе $PM$ являются / отрицательными, то система управления нестабильна .

Системы управления — полярные участки

В предыдущих главах мы обсуждали графики Боде. Там у нас есть два отдельных графика для амплитуды и фазы как функции частоты. Давайте теперь поговорим о полярных участках. Полярный график — это график, который можно нарисовать между величиной и фазой. Здесь величины представлены только нормальными значениями.

Полярная форма $G (j \ omega) H (j \ omega)$

$$ G (J \ омега) H (J \ омега) = | G (J \ омега) H (J \ омега) | \ angle G (j \ omega) H (j \ omega) $$

Полярный график — это график, который можно нарисовать между величиной и фазовым углом $G (j \ omega) H (j \ omega)$, изменяя $\ omega$ от нуля до ∞. Таблица полярного графика показана на следующем рисунке.

Этот график состоит из концентрических кругов и радиальных линий. Концентрические окружности и радиальные линии представляют величины и фазовые углы соответственно. Эти углы представлены положительными значениями в направлении против часовой стрелки. Точно так же мы можем представить углы с отрицательными значениями по часовой стрелке. Например, угол 270 ⁰ в направлении против часовой стрелки равен углу -90 ⁰ в направлении по часовой стрелке.

Правила рисования полярных графиков

Следуйте этим правилам для построения полярных графиков.

• Замените $s = j \ omega$ в передаточной функции без обратной связи.

• Напишите выражения для величины и фазы $G (j \ omega) H (j \ omega)$.

• Найдите начальную величину и фазу $G (j \ omega) H (j \ omega)$, подставив $\ omega = 0$. Итак, полярный график начинается с этой величины и фазового угла.

• Найдите конечную величину и фазу $G (j \ omega) H (j \ omega)$, подставив $\ omega = \ infty$. Итак, полярный график заканчивается этой величиной и фазовым углом.

• Проверьте, пересекает ли полярный график действительную ось, сделав мнимый член $G (j \ omega) H (j \ omega)$ равным нулю, и найдите значение (я) $\ omega$.

• Проверьте, пересекает ли полярный график мнимую ось, сделав реальный член $G (j \ omega) H (j \ omega)$ равным нулю, и найдите значение (я) $\ omega$.

• Для более четкого прорисовки полярного графика найдите величину и фазу $G (j \ omega) H (j \ omega)$, учитывая другие значения $\ omega$.

Замените $s = j \ omega$ в передаточной функции без обратной связи.

Напишите выражения для величины и фазы $G (j \ omega) H (j \ omega)$.

Найдите начальную величину и фазу $G (j \ omega) H (j \ omega)$, подставив $\ omega = 0$. Итак, полярный график начинается с этой величины и фазового угла.

Найдите конечную величину и фазу $G (j \ omega) H (j \ omega)$, подставив $\ omega = \ infty$. Итак, полярный график заканчивается этой величиной и фазовым углом.

Проверьте, пересекает ли полярный график действительную ось, сделав мнимый член $G (j \ omega) H (j \ omega)$ равным нулю, и найдите значение (я) $\ omega$.

Проверьте, пересекает ли полярный график мнимую ось, сделав реальный член $G (j \ omega) H (j \ omega)$ равным нулю, и найдите значение (я) $\ omega$.

Для более четкого прорисовки полярного графика найдите величину и фазу $G (j \ omega) H (j \ omega)$, учитывая другие значения $\ omega$.

пример

Рассмотрим передаточную функцию без обратной связи системы управления с обратной связью.

$$G (s) H (s) = \ гидроразрыва {5} {s (s + 1), (s + 2)}$$

Давайте нарисуем полярный график для этой системы управления, используя приведенные выше правила.

Шаг 1 — Заменить $s = j \ omega$ в передаточной функции без обратной связи.

$$G (J \ омега) Н (J \ омега) = \ гидроразрыва {5} {J \ омега (J \ омега + 1), (J \ омега + 2)}$$

Величина передаточной функции без обратной связи

$$М = \ гидроразрыва {5} {\ Omega (\ SQRT {\ Omega ^ 2 + 1}) (\ SQRT {\ Omega ^ 2 + 4})}$$

Фазовый угол передаточной функции без обратной связи

$$\ Phi = -90 ^ 0- \ загаром ^ {- 1} \ \ загаром омега ^ {- 1} \ гидроразрыва {\ Omega} {2}$$

Шаг 2 — В следующей таблице приведены величина и фазовый угол передаточной функции разомкнутого контура при $\ omega = 0$ рад / с и $\ omega = \ infty$ рад / с.

Частота (рад / сек)	величина	Фазовый угол (градусы)
0	∞	-90 или 270
∞	0	-270 или 90

Итак, полярный график начинается в (∞, −90 ⁰ ) и заканчивается в (0, −270 ⁰ ). Первое и второе слагаемые в скобках указывают величину и фазовый угол соответственно.

Шаг 3 — На основе начальной и конечной полярных координат, этот полярный график будет пересекать отрицательную действительную ось. Фазовый угол, соответствующий отрицательной действительной оси, равен -180 ⁰ или 180 ⁰ . Таким образом, приравнивая фазовый угол передаточной функции разомкнутого контура к -180 ⁰ или 180 ⁰ , мы получим значение $\ omega$ как $\ sqrt {2}$.

Подставляя $\ omega = \ sqrt {2}$ в величину передаточной функции с разомкнутым контуром, мы получим $M = 0.83$. Следовательно, полярный график пересекает отрицательную вещественную ось, когда $\ omega = \ sqrt {2}$ и полярная координата равна (0,83, -180 ⁰ ).

Таким образом, мы можем нарисовать полярный график с приведенной выше информацией на листе полярного графика.

Системы управления — Nyquist Plots

Графики Найквиста являются продолжением полярных графиков для нахождения устойчивости замкнутых систем управления путем изменения ω от −∞ до ∞. Это означает, что графики Найквиста используются для построения полной частотной характеристики передаточной функции с разомкнутым контуром.

Критерий устойчивости Найквиста

Критерий устойчивости Найквиста работает по принципу аргументации . В нем говорится, что если P полюсов и Z нулей заключены в замкнутый путь плоскости s, то соответствующая плоскость $G (s) H (s)$ должна окружать начало координат $P - Z$. Итак, мы можем записать число окружностей N как,

$$N = PZ$$

• Если замкнутый путь вложенной плоскости «s» содержит только полюса, то направление окружения в плоскости $G (s) H (s)$ будет противоположным направлению замкнутого пути в плоскости «s».

• Если замкнутый путь в плоскости «s» содержит только нули, то направление окружности в плоскости $G (s) H (s)$ будет таким же, как направление замкнутого пути в замкнутом пути в «s» самолет.

Если замкнутый путь вложенной плоскости «s» содержит только полюса, то направление окружения в плоскости $G (s) H (s)$ будет противоположным направлению замкнутого пути в плоскости «s».

Если замкнутый путь в плоскости «s» содержит только нули, то направление окружности в плоскости $G (s) H (s)$ будет таким же, как направление замкнутого пути в замкнутом пути в «s» самолет.

Давайте теперь применим принцип аргумента ко всей правой половине плоскости ‘s’, выбрав ее в качестве замкнутого пути. Этот выбранный путь называется контуром Найквиста .

Мы знаем, что система управления с обратной связью устойчива, если все полюсы передаточной функции с обратной связью находятся в левой половине плоскости ‘s’. Таким образом, полюсы передаточной функции с замкнутым контуром — не что иное, как корни характеристического уравнения. При увеличении порядка характеристического уравнения трудно найти корни. Итак, сопоставим эти корни характеристического уравнения следующим образом.

• Поляки характеристического уравнения такие же, как и у полюсов передаточной функции с разомкнутым контуром.

• Нули характеристического уравнения такие же, как и у полюсов передаточной функции замкнутого контура.

Поляки характеристического уравнения такие же, как и у полюсов передаточной функции с разомкнутым контуром.

Нули характеристического уравнения такие же, как и у полюсов передаточной функции замкнутого контура.

Мы знаем, что система управления с разомкнутым контуром стабильна, если в правой половине плоскости ‘s’ нет полюса с разомкнутым контуром.

т. е. $P = 0 \ Rightarrow N = -Z$

Мы знаем, что система управления с обратной связью стабильна, если в правой половине плоскости ‘s’ нет полюса с обратной связью.

т. е. $Z = 0 \ Rightarrow N = P$

Критерий устойчивости Найквиста гласит, что количество окружностей вокруг критической точки (1 + j0) должно быть равно полюсам характеристического уравнения, которое является ничем иным, как полюсами передаточной функции разомкнутого контура в правой половине плоскости ‘s’. Сдвиг начала координат (1 + j0) дает плоскость характеристического уравнения.

Правила рисования графиков Найквиста

Следуйте этим правилам для построения графиков Найквиста.

• Найдите полюсы и нули передаточной функции $G (s) H (s)$ разомкнутой петли в плоскости ‘s’.

• Нарисуйте полярный график, изменяя $\ omega$ от нуля до бесконечности. Если полюс или ноль присутствуют при s = 0, то варьирование $\ omega$ от 0+ до бесконечности для рисования полярного графика.

• Нарисуйте зеркальное изображение приведенного выше полярного графика для значений $\ omega$ в диапазоне от −∞ до нуля (0 ^— при наличии полюса или нуля при s = 0).

• Количество полукругов бесконечного радиуса будет равно числу полюсов или нулей в начале координат. Полукруг бесконечного радиуса начнется в точке, где заканчивается зеркальное отображение полярного графика. И этот полукруг бесконечного радиуса закончится в точке, где начинается полярный график.

Найдите полюсы и нули передаточной функции $G (s) H (s)$ разомкнутой петли в плоскости ‘s’.

Нарисуйте полярный график, изменяя $\ omega$ от нуля до бесконечности. Если полюс или ноль присутствуют при s = 0, то варьирование $\ omega$ от 0+ до бесконечности для рисования полярного графика.

Нарисуйте зеркальное изображение приведенного выше полярного графика для значений $\ omega$ в диапазоне от −∞ до нуля (0 ^— при наличии полюса или нуля при s = 0).

Количество полукругов бесконечного радиуса будет равно числу полюсов или нулей в начале координат. Полукруг бесконечного радиуса начнется в точке, где заканчивается зеркальное отображение полярного графика. И этот полукруг бесконечного радиуса закончится в точке, где начинается полярный график.

После построения графика Найквиста мы можем найти устойчивость замкнутой системы управления с использованием критерия устойчивости Найквиста. Если критическая точка (-1 + j0) лежит вне окружения, то система управления с обратной связью абсолютно устойчива.

Анализ стабильности с использованием графиков Найквиста

Из графиков Найквиста мы можем определить, является ли система управления стабильной, незначительно стабильной или нестабильной, основываясь на значениях этих параметров.

• Усиление частоты и частоты фазового перехода
• Прибыль маржи и фазовая маржа

Фаза пересечения частоты

Частота, с которой график Найквиста пересекает отрицательную действительную ось (фазовый угол равен 180 ⁰ ), называется частотой пересечения фаз . Он обозначается как $\ omega_ {pc}$.

Усиление пересекает частоту

Частота, на которой график Найквиста имеет величину единицу, известна как частота кроссовера усиления . Он обозначается как $\ omega_ {gc}$.

Стабильность системы управления, основанная на соотношении частоты фазового перехода и частоты усиления, указана ниже.

• Если частота перехода фазы $\ omega_ {pc}$ больше частоты перехода коэффициента усиления $\ omega_ {gc}$, то система управления устойчива .

• Если частота перехода фазы $\ omega_ {pc}$ равна частоте перехода усиления $\ omega_ {gc}$, то система управления является минимально устойчивой .

• Если частота фазового перехода $\ omega_ {pc}$ меньше частоты фазового перехода $\ omega_ {gc}$, то система управления неустойчива .

Если частота перехода фазы $\ omega_ {pc}$ больше частоты перехода коэффициента усиления $\ omega_ {gc}$, то система управления устойчива .

Если частота перехода фазы $\ omega_ {pc}$ равна частоте перехода усиления $\ omega_ {gc}$, то система управления является минимально устойчивой .

Если частота фазового перехода $\ omega_ {pc}$ меньше частоты фазового перехода $\ omega_ {gc}$, то система управления неустойчива .

Получить маржу

Запас усиления $GM$ равен обратной величине графика Найквиста на частоте перехода фазы.

$$GM = \ гидроразрыва {1} {M_ {пк}}$$

Где $M_ {pc}$ — это величина в нормальном масштабе на частоте перехода фазы.

Фазовая маржа

Запас по фазе $PM$ равен сумме 180 ⁰ и фазового угла при частоте перехода усиления.

$$PM = 180 ^ 0 + \ Phi_ {дс}$$

Где $\ phi_ {gc}$ — фазовый угол на частоте перехода усиления.

Стабильность системы управления, основанная на связи между запасом усиления и запасом по фазе, указана ниже.

• Если запас усиления $GM$ больше единицы и запас по фазе $PM$ положителен, то система управления стабильна .

• Если запас усиления $GM$ равен единице, а запас по фазе $PM$ равен нулю градусов, то система управления незначительно устойчива .

• Если запас усиления $GM$ меньше единицы и / или запас по фазе $PM$ отрицателен, то система управления нестабильна .

Если запас усиления $GM$ больше единицы и запас по фазе $PM$ положителен, то система управления стабильна .

Если запас усиления $GM$ равен единице, а запас по фазе $PM$ равен нулю градусов, то система управления незначительно устойчива .

Если запас усиления $GM$ меньше единицы и / или запас по фазе $PM$ отрицателен, то система управления нестабильна .

Системы управления — Компенсаторы

Существует три типа компенсаторов — компенсаторы запаздывания, опережения и опережения. Это наиболее часто используемые.

Компенсатор запаздывания

Компенсатор запаздывания представляет собой электрическую сеть, которая выдает синусоидальный выходной сигнал, имеющий фазовый запаздывание при применении синусоидального входного сигнала. Схема компенсатора запаздывания в области ‘s’ показана на следующем рисунке.

Здесь конденсатор подключен последовательно с резистором $R_2$, и выход измеряется по этой комбинации.

Передаточная функция этого компенсатора запаздывания —

$$\ frac {V_o (s)} {V_i (s)} = \ frac {1} {\ alpha} \ left (\ frac {s + \ frac {1} {\ tau}} {s + \ frac {1} {\ alpha \ tau}} \ right)$$

Куда,

$$\ тау = R_2C$$

$$\ альфа = \ гидроразрыва {R_1 + r_2} {R_2}$$

Из приведенного выше уравнения $\ alpha$ всегда больше единицы.

Из передаточной функции можно сделать вывод, что компенсатор запаздывания имеет один полюс в $s = - \ frac {1} {\ alpha \ tau}$ и один ноль в $s = - \ frac {1} {\ tau}$ , Это означает, что полюс будет ближе к началу координат в конфигурации нулевой полюс компенсатора запаздывания.

Замените $s = j \ omega$ в передаточной функции.

$$\ frac {V_o (j \ omega)} {V_i (j \ omega)} = \ frac {1} {\ alpha} \ left (\ frac {j \ omega + \ frac {1} {\ tau}} { j \ omega + \ frac {1} {\ alpha \ tau}} \ right)$$

Фазовый угол $\ phi = \ tan ^ {- 1} \ omega \ tau - tan ^ {- 1} \ alpha \ omega \ tau$

Известно, что фаза выходного синусоидального сигнала равна сумме фазовых углов входного синусоидального сигнала и передаточной функции.

Таким образом, для получения фазового запаздывания на выходе этого компенсатора фазовый угол передаточной функции должен быть отрицательным. Это произойдет, когда $\ alpha&amp;gt; 1$.

Ведущий компенсатор

Компенсатор вывода представляет собой электрическую сеть, которая выдает синусоидальный выход, имеющий фазовый вывод, когда применяется синусоидальный вход. Схема ведущего компенсатора в области ‘s’ показана на следующем рисунке.

Здесь конденсатор параллелен резистору $R_1$, и выход измеряется через резистор $ R_2.

Передаточная функция этого ведущего компенсатора —

$$\ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau + 1} {\ beta s \ tau + 1} \ right)$$

Куда,

$$\ тау = R_1C$$

$$\ бета = \ гидроразрыва {R_2} {R_1 + R_2}$$

Из передаточной функции мы можем заключить, что ведущий компенсатор имеет полюс в $s = - \ frac {1} {\ beta}$ и ноль в $s = - \ frac {1} {\ beta \ tau}$.

Замените $s = j \ omega$ в передаточной функции.

$$\ frac {V_o (j \ omega)} {V_i (j \ omega)} = \ beta \ left (\ frac {j \ omega \ tau + 1} {\ beta j \ omega \ tau + 1} \ right )$$

Фазовый угол $\ phi = tan ^ {- 1} \ omega \ tau - tan ^ {- 1} \ beta \ omega \ tau$

Известно, что фаза выходного синусоидального сигнала равна сумме фазовых углов входного синусоидального сигнала и передаточной функции.

Таким образом, для получения фазового опережения на выходе этого компенсатора фазовый угол передаточной функции должен быть положительным. Это произойдет, когда $0 &amp;lt;\ beta &amp;lt;1$. Следовательно, ноль будет ближе к началу в конфигурации нулевого полюса ведущего компенсатора.

Компенсатор запаздывания

Компенсатор запаздывания — это электрическая сеть, которая производит запаздывание фазы в одной частотной области и опережение фазы в другой частотной области. Это сочетание компенсаторов запаздывания и опережения. Схема компенсатора запаздывания в области ‘s’ показана на следующем рисунке.

Эта схема выглядит так, как оба компенсатора расположены каскадом. Таким образом, передаточная функция этой схемы будет являться произведением передаточных функций опережения и компенсаторов запаздывания.

$$\ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau_1 + 1} {\ beta s \ tau_1 + 1} \ right) \ frac {1} {\ альфа} \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right)$$

Мы знаем, что $\ alpha \ beta = 1$.

$$\ Rightarrow \ frac {V_o (s)} {V_i (s)} = \ left (\ frac {s + \ frac {1} {\ tau_1}} {s + \ frac {1} {\ beta \ tau_1}} \ right) \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right)$$

Куда,

$$\ tau_1 = R_1C_1$$

$$\ tau_2 = R_2C_2$$

Системы управления — контроллеры

Различные типы контроллеров используются для повышения производительности систем управления. В этой главе мы обсудим основные контроллеры, такие как пропорциональный, производный и интегральный контроллеры.

Пропорциональный контроллер

Пропорциональный контроллер выдает выходной сигнал, который пропорционален сигналу ошибки.

$$u (t) \ propto e (t)$$

$$\ Rightarrow u (t) = K_P e (t)$$

Применить преобразование Лапласа с обеих сторон —

$$U (s) = K_P E (s)$$

$$\ гидроразрыва {U (s)} {Е (с)} = K_P$$

Следовательно, передаточная функция пропорционального регулятора равна $K_P$.

Куда,

U (s) — преобразование Лапласа управляющего сигнала u (t)

E (s) — преобразование Лапласа сигнала ошибки e (t)

K _P — константа пропорциональности

Блок-схема системы управления замкнутым контуром с отрицательной обратной связью вместе с пропорциональным регулятором показана на следующем рисунке.

Пропорциональный регулятор используется для изменения переходного процесса в соответствии с требованием.

Производный контроллер

Производный контроллер выдает выход, который является производным от сигнала ошибки.

$$u (t) = K_D \ frac {\ text {d} e (t)} {\ text {d} t}$$

Примените преобразование Лапласа с обеих сторон.

$$U (s) = K_D sE (s)$$

$$\ frac {U (s)} {E (s)} = K_D s$$

Следовательно, передаточная функция производного контроллера равна $K_D s$.

Где $K_D$ — производная константа.

Блок-схема единой системы управления с обратной связью и обратной связью вместе с производным контроллером показана на следующем рисунке.

Производный контроллер используется для превращения нестабильной системы управления в стабильную.

Интегральный контроллер

Интегральный контроллер выдает выходной сигнал, который является интегралом от сигнала ошибки.

$$u (t) = K_I \ int e (t) dt$$

Применить преобразование Лапласа с обеих сторон —

$$U (s) = \ frac {K_I E (s)} {s}$$

$$\ гидроразрыва {U (s)} {Е (ы)} = \ гидроразрыва {K_i} {s}$$

Следовательно, передаточная функция интегрального контроллера равна $\ frac {K_I} {s}$.

Где $K_I$ — интегральная постоянная.

Блок-схема единой системы управления с обратной связью и обратной связью вместе со встроенным контроллером показана на следующем рисунке.

Встроенный контроллер используется для уменьшения ошибки установившегося состояния.

Давайте теперь поговорим о комбинации основных контроллеров.

Пропорциональный производный (PD) контроллер

Пропорциональный производный контроллер создает выход, который представляет собой комбинацию выходов пропорционального и производного контроллеров.

$$u (t) = K_P e (t) + K_D \ frac {\ text {d} e (t)} {\ text {d} t}$$

Применить преобразование Лапласа с обеих сторон —

$$U (s) = (K_P + K_D s) E (s)$$

$$\ frac {U (s)} {E (s)} = K_P + K_D s$$

Следовательно, передаточная функция контроллера пропорциональной производной равна $K_P + K_D s$.

Блок-схема системы управления замкнутого контура с отрицательной обратной связью и контроллера пропорциональной производной показана на следующем рисунке.

Пропорциональный регулятор производной используется для улучшения стабильности системы управления без влияния на ошибку установившегося состояния.

Пропорциональный интегральный (ПИ) контроллер

Пропорциональный интегральный контроллер создает выход, который представляет собой комбинацию выходов пропорционального и интегрального контроллеров.

$$u (t) = K_P e (t) + K_I \ int e (t) dt$$

Применить преобразование Лапласа с обеих сторон —

$$U (s) = \ left (K_P + \ frac {K_I} {s} \ right) E (s)$$

$$\ гидроразрыва {U (s)} {Е (с)} = K_P + \ гидроразрыва {K_i} {s}$$

Следовательно, передаточная функция пропорционального интегрального регулятора равна $K_P + \ frac {K_I} {s}$.

Блок-схема системы управления замкнутого контура с отрицательной обратной связью вместе с пропорциональным интегральным контроллером показана на следующем рисунке.

Пропорциональный интегральный регулятор используется для уменьшения ошибки установившегося состояния без влияния на стабильность системы управления.

Пропорциональный интегрально-производный (PID) контроллер

Пропорциональный интегрально-производный контроллер создает выход, который представляет собой комбинацию выходов пропорционального, интегрального и производного контроллеров.

$$u (t) = K_P e (t) + K_I \ int e (t) dt + K_D \ frac {\ text {d} e (t)} {\ text {d} t}$$

Применить преобразование Лапласа с обеих сторон —

$$U (s) = \ left (K_P + \ frac {K_I} {s} + K_D s \ right) E (s)$$

$$\ frac {U (s)} {E (s)} = K_P + \ frac {K_I} {s} + K_D s$$

Следовательно, передаточная функция контроллера пропорциональной интегральной производной равна $K_P + \ frac {K_I} {s} + K_D s$.

Блок-схема системы управления замкнутого контура с отрицательной обратной связью вместе с пропорционально-интегральным регулятором производной показана на следующем рисунке.

Пропорциональный интегрально-производный регулятор используется для улучшения стабильности системы управления и уменьшения ошибки установившегося состояния.

Системы управления — государственная космическая модель

Модель пространства состояний системы линейного инварианта времени (LTI) может быть представлена ​​как

$$\ точка {X} = AX + BU$$

$$Y = CX + DU$$

Первое и второе уравнения известны как уравнение состояния и выходное уравнение соответственно.

Куда,

• X и $\ dot {X}$ — вектор состояния и вектор дифференциального состояния соответственно.

• U и Y — входной вектор и выходной вектор соответственно.

• А — системная матрица.

• B и C — входная и выходная матрицы.

• D — матрица прямой связи.

X и $\ dot {X}$ — вектор состояния и вектор дифференциального состояния соответственно.

U и Y — входной вектор и выходной вектор соответственно.

А — системная матрица.

B и C — входная и выходная матрицы.

D — матрица прямой связи.

Основные понятия государственной космической модели

Следующая основная терминология используется в этой главе.

государственный

Это группа переменных, которая суммирует историю системы, чтобы предсказать будущие значения (результаты).

Государственная переменная

Количество требуемых переменных состояния равно количеству элементов хранения, присутствующих в системе.

Примеры — ток, протекающий через индуктор, напряжение на конденсаторе

Государственный вектор

Это вектор, который содержит переменные состояния в качестве элементов.

В предыдущих главах мы обсудили две математические модели систем управления. Это модель дифференциального уравнения и модель передаточной функции. Модель пространства состояний может быть получена из любой из этих двух математических моделей. Давайте теперь обсудим эти два метода один за другим.

Модель пространства состояний из дифференциального уравнения

Рассмотрим следующую серию схемы RLC. Он имеет входное напряжение, $v_i (t)$, а ток, протекающий по цепи, составляет $i (t)$.

В этой схеме есть два накопителя (индуктор и конденсатор). Таким образом, число переменных состояния равно двум, и этими переменными состояния являются ток, протекающий через индуктор, $i (t)$ и напряжение на конденсаторе, $v_c (t)$.

Из схемы выходное напряжение $v_0 (t)$ равно напряжению на конденсаторе, $v_c (t)$.

$$v_0 (т) = v_c (т)$$

Примените КВЛ вокруг петли.

$$v_i (т) = Ri (т) + L \ гидроразрыва {\ текст {d} я (т)} {\ текст {d} т} + v_c (т)$$

$$\ Rightarrow \ frac {\ text {d} i (t)} {\ text {d} t} = - \ frac {Ri (t)} {L} - \ frac {v_c (t)} {L} + \ гидроразрыва {v_i (т)} {L}$$

Напряжение на конденсаторе составляет —

$$v_c (t) = \ frac {1} {C} \ int i (t) dt$$

Дифференцируйте вышеприведенное уравнение по времени.

$$\ гидроразрыва {\ текст {d} v_c (т)} {\ текст {d} т} = \ {гидроразрыва я (т)} {C},$$

Вектор состояния, $X = \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix}$

Вектор дифференциального состояния, $\ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t )} {\ text {d} t} \ end {bmatrix}$

Мы можем организовать дифференциальные уравнения и выходное уравнение в стандартную форму модели пространства состояний как,

$$\ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t)} { \ text {d} t} \ end {bmatrix} = \ begin {bmatrix} - \ frac {R} {L} &amp;amp; - \ frac {1} {L} \\\ frac {1} {C} &amp;amp; 0 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} + \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix} \ begin {bmatrix } v_i (t) \ end {bmatrix}$$

$$Y = \ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix}$$

Куда,

$$A = \ begin {bmatrix} - \ frac {R} {L} &amp;amp; - \ frac {1} {L} \\\ frac {1} {C} &amp;amp; 0 \ end {bmatrix}, \: B = \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix}, \: C = \ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \: и \: D = \ begin {bmatrix } 0 \ end {bmatrix}$$

Модель пространства состояний из передаточной функции

Рассмотрим два типа передаточных функций, основанные на типе терминов, присутствующих в числителе.

• Передаточная функция с постоянным членом в Числителе.
• Передаточная функция, имеющая полиномиальную функцию ‘s’ в Числителе.

Передаточная функция с постоянным членом в Числителе

Рассмотрим следующую передаточную функцию системы

$$ \ гидроразрыва {Y (s)} {U (s)} = \ {гидроразрыва b_0} {s ^ п + a_ {п-1} s ^ {п-1} + … + a_1s + A_0} $ $

Переставить приведенное выше уравнение как

$$(s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) Y (s) = b_0 U (s)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} + а_ {п-1} \ гидроразрыва {\ текст {d} ^ {N-1} у (т )} {\ текст {d} т ^ {N-1}} + ... a_1 \ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} + a_0y (т) = B_0 и (т)$$

Позволять

$$у (г) = x_1$$

$$\ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} = x_2 = \ точка {х} -1$$

$$\ гидроразрыва {\ текст {d} ^ 2у (т)} {\ текст {d} т ^ 2} = x_3 = \ точка {х} _2$$

.

.

.

$$ \ гидроразрыва {\ текст {d} ^ {N-1} у (г)} {\ текст {d} т ^ {N-1}} = x_n = \ точки {х} _ {п-1} $ $

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} = \ точка {х} _n$$

и $u (t) = u$

Затем,

$$\ dot {x} _n + a_ {n-1} x_n + ... + a_1x_2 + a_0x_1 = b_0 u$$

Из приведенного выше уравнения мы можем написать следующее уравнение состояния.

$$\ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + b_0 u$$

Выходное уравнение —

$$у (г) = у = x_1$$

Модель пространства состояний —

$\ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix}$

$$= \ begin {bmatrix} 0 &amp;amp; 1 &amp;amp; 0 &amp;amp; \ dotso &amp;amp; 0 &amp;amp; 0 \\ 0 &amp;amp; 0 &amp;amp; 1 &amp;amp; \ dotso &amp;amp; 0 &amp;amp; 0 \\\ vdots &amp;amp; \ vdots &amp;amp; \ vdots &amp;amp; \ dotso &amp;amp; \ vdots &amp;amp; \ vdots \\ 0 &amp;amp; 0 &amp;amp; 0 &amp;amp; \ dotso &amp;amp; 0 &amp;amp; 1 \\ - a_0 &amp;amp; -a_1 &amp;amp; -a_2 &amp;amp; \ dotso &amp;amp; -a_ {n-2} &amp;amp; -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix}$$

$$Y = \ begin {bmatrix} 1 &amp;amp; 0 &amp;amp; \ dotso &amp;amp; 0 &amp;amp; 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix}$$

Здесь $D = \ left [0 \ right].$

пример

Найти модель пространства состояний для системы, имеющей передаточную функцию.

$$\ гидроразрыва {Y (ы)} {U (ы)} = \ гидроразрыва {1} {S ^ 2 + S + 1}$$

Переставить, приведенное выше уравнение как,

$$(S ^ 2 + S + 1) Y (s) = U (ы)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$\ гидроразрыва {\ текст {d} ^ 2у (т)} {\ текст {d} т ^ 2} + \ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} + у (т) = U (T)$$

Позволять

$$у (г) = x_1$$

$$\ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} = x_2 = \ точка {х} -1$$

и $u (t) = u$

Тогда уравнение состояния

$$\ точка {х} _2 = -x_1-x_2 + и$$

Выходное уравнение

$$у (г) = у = x_1$$

Модель пространства состояний

$$\ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} 0 &amp;amp; 1 \\ - 1 &amp;amp; -1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} \ left [u \ right]$$

$$Y = \ begin {bmatrix} 1 &amp;amp; 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix}$$

Передаточная функция, имеющая полиномиальную функцию ‘s’ в Числителе

Рассмотрим следующую передаточную функцию системы

$$\ frac {Y (s)} {U (s)} = \ frac {b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0}$$

$$\ Rightarrow \ frac {Y (s)} {U (s)} = \ left (\ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} \ right) (b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0)$$

Вышеупомянутое уравнение имеет вид произведения передаточных функций двух блоков, которые расположены каскадом.

$$\ frac {Y (s)} {U (s)} = \ left (\ frac {V (s)} {U (s)} \ right) \ left (\ frac {Y (s)} {V (s)} \ right)$$

Вот,

$$\ frac {V (s)} {U (s)} = \ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0}$$

Переставить приведенное выше уравнение как

$$(ы ^ п + а_ {п-1} с ^ {N-1} + ... A_0) V (S) = U (ы)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} + а_ {п-1} \ гидроразрыва {\ текст {d} ^ {N-1} v (т )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} v (t)} {\ text {d} t} + a_0v (t) = u (т)$$

Позволять

$$V (T) = x_1$$

$$\ гидроразрыва {\ текст {d} v ((т)} {\ текст {d} т} = x_2 = \ точка {х} -1$$

$$\ гидроразрыва {\ текст {d} ^ 2v (т)} {\ текст {d} т ^ 2} = x_3 = \ точки {х} _2$$

.

.

.

$$ \ гидроразрыва {\ текст {d} ^ {N-1} V (T)} {\ текст {d} т ^ {N-1}} = x_n = \ точка {х} _ {п-1} $ $

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} = \ точка {х} _n$$

и $u (t) = u$

Тогда уравнение состояния

$$\ точка {х} _n = -a_0x_1-a_1x_2 -...- а_ {п-1} x_n + U$$

Рассматривать,

$$\ гидроразрыва {Y (s)} {V (S)} = b_ns ^ п + B_ {п-1} с ^ {N-1} + ... + b_1s B_0$$

Переставить приведенное выше уравнение как

$$Y (s) = (b_ns ^ п + B_ {п-1} с ^ {N-1} + ... + b_1s B_0) V (S)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$у (г) = b_n \ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} + B_ {п-1} \ гидроразрыва {\ текст {d} ^ {п -1} V (T)} {\ текст {d} т ^ {N-1}} + ... b_1 \ гидроразрыва {\ текст {d} v (т)} {\ текст {d} т} + b_0v (т)$$

Подставляя переменные состояния и $y (t) = y$ в вышеприведенном уравнении, получим выходное уравнение как,

$$у = b_n \ точка {х} _n + b_ {п-1} x_n + ... + b_1x_2 + b_0x_1$$

Замените значение $\ dot {x} _n$ в приведенном выше уравнении.

$$у = b_n (-a_0x_1-a_1x_2 -...- а_ {п-1} x_n + и) + B_ {п-1} x_n + ... + b_1x_2 b_0x_1$$

$$y = (b_0-b_na_0) x_1 + (b_1-b_na_1) x_2 + ... + (b_ {n-1} -b_na_ {n-1}) x_n + b_n u$$

Модель пространства состояний

$\ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix}$

$$= \ begin {bmatrix} 0 &amp;amp; 1 &amp;amp; 0 &amp;amp; \ dotso &amp;amp; 0 &amp;amp; 0 \\ 0 &amp;amp; 0 &amp;amp; 1 &amp;amp; \ dotso &amp;amp; 0 &amp;amp; 0 \\\ vdots &amp;amp; \ vdots &amp;amp; \ vdots &amp;amp; \ dotso &amp;amp; \ vdots &amp;amp; \ vdots \\ 0 &amp;amp; 0 &amp;amp; 0 &amp;amp; \ dotso &amp;amp; 0 &amp;amp; 1 \\ - a_0 &amp;amp; -a_1 &amp;amp; -a_2 &amp;amp; \ dotso &amp;amp; -a_ {n-2} &amp;amp; -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix}$$

$$Y = [b_0-b_na_0 \ quad b_1-b_na_1 \ quad ... \ quad b_ {n-2} -b_na_ {n-2} \ quad b_ {n-1} -b_na_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix}$$

Если $b_n = 0$, то

$$Y = [b_0 \ quad b_1 \ quad ... \ quad b_ {n-2} \ quad b_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n- 1} \\ x_n \ end {bmatrix}$$

Системы управления — анализ состояния пространства

В предыдущей главе мы узнали, как получить модель пространства состояний из дифференциального уравнения и передаточной функции. В этой главе мы обсудим, как получить передаточную функцию из модели пространства состояний.

Передаточная функция из модели пространства состояний

Мы знаем, что модель пространства состояний линейной инвариантной по времени системы (LTI) —

$$\ точка {X} = AX + BU$$

$$Y = CX + DU$$

Примените преобразование Лапласа с обеих сторон уравнения состояния.

$$Sx (s) = АХ (тв) + Bu (ы)$$

$$\ Rightarrow (sI-A) X (s) = BU (s)$$

$$\ Rightarrow X (s) = (sI-A) ^ {- 1} BU (s)$$

Примените преобразование Лапласа с обеих сторон выходного уравнения.

$$Y (s) = СХ (тв) + DU (ы)$$

Подставьте значение X (s) в приведенном выше уравнении.

$$\ Rightarrow Y (s) = C (sI-A) ^ {- 1} BU (s) + DU (s)$$

$$\ Rightarrow Y (s) = [C (sI-A) ^ {- 1} B + D] U (s)$$

$$\ Rightarrow \ frac {Y (s)} {U (s)} = C (sI-A) ^ {- 1} B + D$$

Вышеупомянутое уравнение представляет передаточную функцию системы. Таким образом, мы можем вычислить передаточную функцию системы, используя эту формулу для системы, представленной в модели пространства состояний.

Примечание. Когда $D = [0]$, передаточная функция будет

$$\ гидроразрыва {Y (s)} {U (s)} = С (Si-А) ^ {- 1} В$$

пример

Рассчитаем передаточную функцию системы, представленной в модели пространства состояний, как,

$$\ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 &amp;amp; -1 \\ 1 &amp;amp; 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u]$$

$$Y = \ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix}$$

Вот,

$$A = \ begin {bmatrix} -1 &amp;amp; -1 \\ 1 &amp;amp; 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad C = \ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \ quad и \ quad D = [0]$$

Формула для передаточной функции при $D = [0]$ равна —

$$\ гидроразрыва {Y (s)} {U (s)} = С (Si-А) ^ {- 1} В$$

Замените матрицы A, B и C в приведенном выше уравнении.

$$\ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \ begin {bmatrix} s + 1 &amp;amp; 1 \\ - 1 &amp;amp; s \ end {bmatrix } ^ {- 1} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}$$

$$\ Rightarrow \ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \ frac {\ begin {bmatrix} s &amp;amp; -1 \\ 1 &amp;amp; s + 1 \ end {bmatrix}} {(s + 1) s-1 (-1)} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}$$

$$\ Rightarrow \ frac {Y (s)} {U (s)} = \ frac {\ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \ begin {bmatrix} s \\ 1 \ end {bmatrix}} {s ^ 2 + s + 1} = \ гидроразрыва {1} {s ^ 2 + s + 1}$$

Следовательно, передаточная функция системы для данной модели пространства состояний

$$\ гидроразрыва {Y (ы)} {U (ы)} = \ гидроразрыва {1} {S ^ 2 + S + 1}$$

Матрица государственных переходов и ее свойства

Если система имеет начальные условия, она выдаст результат. Так как этот вывод присутствует даже при отсутствии ввода, он называется нулевым входным откликом $x_ {ZIR} (t)$. Математически мы можем записать это как

$$x_ {ZIR} (t) = e ^ {At} X (0) = L ^ {- 1} \ left \ {\ left [sI-A \ right] ^ {- 1} X (0) \ right \}$$

Из приведенного выше соотношения можно записать матрицу перехода состояний $\ phi (t)$ в виде

$$\ Phi (т) = е ^ {В} = L ^ {- 1} [Si-А] ^ {- 1}$$

Таким образом, нулевой входной отклик может быть получен умножением матрицы перехода состояний $\ phi (t)$ на матрицу начальных условий.

Ниже приведены свойства матрицы перехода состояний.

• Если $t = 0$, то матрица перехода состояний будет равна матрице идентичности.

  $$\ phi (0) = I$$

• Обратная матрица перехода состояний будет такой же, как и матрица перехода состояний, просто заменив ‘t’ на ‘-t’.

  $$\ phi ^ {- 1} (t) = \ phi (−t)$$

• Если $t = t_1 + t_2$, то соответствующая матрица перехода состояний равна умножению двух матриц перехода состояний при $t = t_1$ и $t = t_2$.

  $$\ phi (t_1 + t_2) = \ phi (t_1) \ phi (t_2)$$

Если $t = 0$, то матрица перехода состояний будет равна матрице идентичности.

$$\ phi (0) = I$$

Обратная матрица перехода состояний будет такой же, как и матрица перехода состояний, просто заменив ‘t’ на ‘-t’.

$$\ phi ^ {- 1} (t) = \ phi (−t)$$

Если $t = t_1 + t_2$, то соответствующая матрица перехода состояний равна умножению двух матриц перехода состояний при $t = t_1$ и $t = t_2$.

$$\ phi (t_1 + t_2) = \ phi (t_1) \ phi (t_2)$$

Управляемость и наблюдаемость

Давайте теперь обсудим управляемость и наблюдаемость системы управления один за другим.

контролируемость

Говорят, что система управления является управляемой, если начальные состояния системы управления переводятся (изменяются) в некоторые другие требуемые состояния с помощью управляемого входа за конечную продолжительность.

Мы можем проверить управляемость системы управления с помощью теста Калмана .

• Запишите матрицу $Q_c$ в следующем виде.

  $$Q_c = \ left [B \ quad AB \ quad A ^ 2B \ quad ... \ quad A ^ {n-1} B \ right]$$

• Найти определитель матрицы $Q_c$ и, если он не равен нулю, то система управления является управляемой.

Запишите матрицу $Q_c$ в следующем виде.

$$Q_c = \ left [B \ quad AB \ quad A ^ 2B \ quad ... \ quad A ^ {n-1} B \ right]$$

Найти определитель матрицы $Q_c$ и, если он не равен нулю, то система управления является управляемой.

возможность наблюдения

Считается, что система управления является наблюдаемой, если она способна определять начальные состояния системы управления, наблюдая за выходами в течение конечного промежутка времени.

Мы можем проверить наблюдаемость системы управления с помощью теста Калмана .

• Запишите матрицу $Q_o$ в следующем виде.

  $$Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ quad (A ^ T) ^ 2C ^ T \ quad ... \ quad (A ^ T) ^ {n-1} C ^ T \ правильно]$$

• Найти определитель матрицы $Q_o$ и, если она не равна нулю, то система управления наблюдаема.

Запишите матрицу $Q_o$ в следующем виде.

$$Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ quad (A ^ T) ^ 2C ^ T \ quad ... \ quad (A ^ T) ^ {n-1} C ^ T \ правильно]$$

Найти определитель матрицы $Q_o$ и, если она не равна нулю, то система управления наблюдаема.

пример

Давайте проверим управляемость и наблюдаемость системы управления, которая представлена ​​в модели пространства состояний как,

$$\ dot {x} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 &amp;amp; -1 \\ 1 &amp;amp; 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u]$$

$$Y = \ begin {bmatrix} 0 &amp;amp; 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix}$$

Вот,

$$A = \ begin {bmatrix} -1 &amp;amp; -1 \\ 1 &amp;amp; 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad \ begin {bmatrix } 0 &amp;amp; 1 \ end {bmatrix}, D = [0] \ quad и \ quad n = 2$$

Для $n = 2$ матрица $Q_c$ будет

$$Q_c = \ left [B \ quad AB \ right]$$

Мы получим произведение матриц A и B как,

$$AB = \ begin {bmatrix} -1 \\ 1 \ end {bmatrix}$$

$$\ Rightarrow Q_c = \ begin {bmatrix} 1 &amp;amp; -1 \\ 0 &amp;amp; 1 \ end {bmatrix}$$

$$| Q_c | = 1 \ neq 0$$

Поскольку определитель матрицы $Q_c$ не равен нулю, данная система управления является управляемой.

Для $n = 2$ матрица $Q_o$ будет иметь вид —

$$Q_o = \ left [C ^ T \ quad A ^ TC ^ T \ right]$$

Вот,

$$ A ^ T = \ begin {bmatrix} -1 & 1 \\ — 1 & 0 \ end {bmatrix} \ quad и \ quad C ^ T = \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} $ $

Мы получим произведение матриц $A ^ T$ и $C ^ T$ как

$$A ^ TC ^ T = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}$$

$$\ Rightarrow Q_o = \ begin {bmatrix} 0 &amp;amp; 1 \\ 1 &amp;amp; 0 \ end {bmatrix}$$

$$\ Rightarrow | Q_o | = -1 \ quad \ neq 0$$

Поскольку определитель матрицы $Q_o$ не равен нулю, данная система управления наблюдаема.

Следовательно, данная система управления является одновременно управляемой и наблюдаемой.