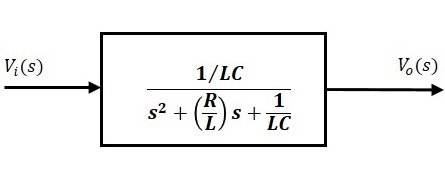Системы управления — математические модели

Системы управления могут быть представлены с помощью ряда математических уравнений, известных как математическая модель . Эти модели полезны для анализа и проектирования систем управления. Анализ системы управления означает поиск выхода, когда мы знаем вход и математическую модель. Проектирование системы управления означает поиск математической модели, когда мы знаем вход и выход.

В основном используются следующие математические модели.

• Модель дифференциального уравнения
• Модель передаточной функции
• Государственная космическая модель

Давайте обсудим первые две модели в этой главе.

Модель дифференциального уравнения

Модель дифференциальных уравнений представляет собой математическую модель систем управления во временной области. Выполните следующие шаги для модели дифференциального уравнения.

• Применять основные законы к данной системе управления.

• Получите дифференциальное уравнение с точки зрения ввода и вывода, исключив промежуточную переменную (и).

Применять основные законы к данной системе управления.

Получите дифференциальное уравнение с точки зрения ввода и вывода, исключив промежуточную переменную (и).

пример

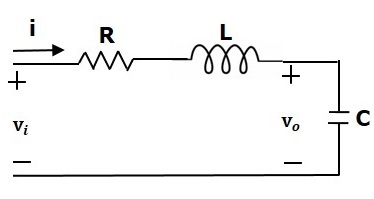
Рассмотрим следующую электрическую систему, как показано на следующем рисунке. Эта схема состоит из резистора, катушки индуктивности и конденсатора. Все эти электрические элементы соединены последовательно . Входное напряжение, приложенное к этой схеме, составляет $v_i$, а напряжение на конденсаторе — это выходное напряжение $v_o$.

Сетчатое уравнение для этой схемы

$$v_i = Ri + L \ гидроразрыва {\ текст {d} я} {\ текст {d} т} + v_o$$

Подставим ток, проходящий через конденсатор $i = c \ frac {\ text {d} v_o} {\ text {d} t}$ в приведенном выше уравнении.

 Rightarrowvi=RC гидроразрыва текстdvo текстdт+LC гидроразрыва текстd2vo текстdт2+vo $$\ Rightarrow \: v_i = RC \ гидроразрыва {\ текст {d} v_o} {\ текст {d} т} + LC \ гидроразрыва {\ текст {d} ^ 2v_o} {\ текст {d} т ^ 2} + v_o$$

$$\ Rightarrow \ frac {\ text {d} ^ 2v_o} {\ text {d} t ^ 2} + \ left (\ frac {R} {L} \ right) \ frac {\ text {d} v_o} {\ text {d} t} + \ left (\ frac {1} {LC} \ right) v_o = \ left (\ frac {1} {LC} \ right) v_i$$

Вышеупомянутое уравнение является дифференциальным уравнением второго порядка.

Модель передаточной функции

Модель передаточной функции — это математическая модель систем управления в s-области. Передаточная функция системы с линейным инвариантом времени (LTI) определяется как отношение преобразования Лапласа на выходе и преобразования Лапласа на входе при условии, что все начальные условия равны нулю.

Если $x (t)$ и $y (t)$ являются входом и выходом системы LTI, то соответствующие преобразования Лапласа равны $X (s)$ и $Y (s)$.

Следовательно, передаточная функция системы LTI равна отношению $Y (s)$ и $X (s)$.

ie,TransferFunction= fracY(s)X(s) $$ie, \: Transfer \: Function = \ frac {Y (s)} {X (s)}$$

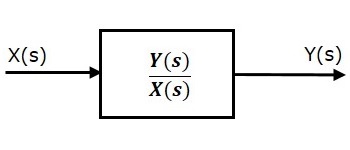
Модель передаточной функции системы LTI показана на следующем рисунке.

Здесь мы представили систему LTI с блоком, имеющим передаточную функцию внутри нее. И этот блок имеет вход $X (s)$ и вывод $Y (s)$.

пример

Ранее мы получили дифференциальное уравнение электрической системы в виде

$$\ frac {\ text {d} ^ 2v_o} {\ text {d} t ^ 2} + \ left (\ frac {R} {L} \ right) \ frac {\ text {d} v_o} {\ текст {d} t} + \ left (\ frac {1} {LC} \ right) v_o = \ left (\ frac {1} {LC} \ right) v_i$$

Примените преобразование Лапласа с обеих сторон.

$$s ^ 2V_o (s) + \ left (\ frac {sR} {L} \ right) V_o (s) + \ left (\ frac {1} {LC} \ right) V_o (s) = \ left ( \ frac {1} {LC} \ right) V_i (s)$$

$$\ Rightarrow \ left \ {s ^ 2 + \ left (\ frac {R} {L} \ right) s + \ frac {1} {LC} \ right \} V_o (s) = \ left (\ frac { 1} {LC} \ right) V_i (s)$$

$$\ Rightarrow \ frac {V_o (s)} {V_i (s)} = \ frac {\ frac {1} {LC}} {s ^ 2 + \ left (\ frac {R} {L} \ right) s + \ гидроразрыва {1} {LC}}$$

Куда,

• $v_i (s)$ — преобразование Лапласа входного напряжения $v_i$

• $v_o (s)$ — преобразование Лапласа выходного напряжения $v_o$

$v_i (s)$ — преобразование Лапласа входного напряжения $v_i$

$v_o (s)$ — преобразование Лапласа выходного напряжения $v_o$

Вышеупомянутое уравнение является передаточной функцией электрической системы второго порядка. Модель передаточной функции этой системы показана ниже.

Здесь мы показываем электрическую систему второго порядка с блоком, имеющим передаточную функцию внутри него. И этот блок имеет вход $V_i (s)$ и выход $V_o (s)$.