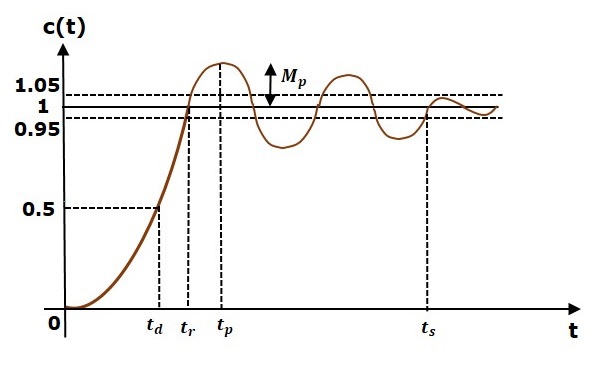
В этой главе давайте обсудим спецификации временной области системы второго порядка. Ответ шага системы второго порядка для случая недостаточной амортизации показан на следующем рисунке.
Все спецификации домена времени представлены на этом рисунке. Отклик до времени установления известен как переходный отклик, а отклик после времени установления называется устойчивым откликом.
Время задержки
Это время, необходимое для того, чтобы ответ достиг половины своего окончательного значения с нулевого момента. Обозначается $ t_d $.
Рассмотрим пошаговый отклик системы второго порядка для t ≥ 0, когда δ лежит между нулем и единицей.
$$ c (t) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta) $$
Окончательное значение шага ответа равно единице.
Следовательно, при $ t = t_d $ значение шага отклика будет 0,5. Подставим эти значения в приведенное выше уравнение.
$$ c (t_d) = 0.5 = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt_d}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_d + \ theta) $$
$$ \ Rightarrow \ left (\ frac {e ^ {- \ delta \ omega_nt_d}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_d + \ theta) = 0,5 $$
Используя линейное приближение, вы получите время задержки t d как
$$ T_d = \ гидроразрыва {1 + 0,7 \ дельта} {\ omega_n} $$
Время нарастания
Это время, необходимое для отклика, чтобы подняться с 0% до 100% от его окончательного значения . Это применимо для систем с недостаточным демпфированием . Для систем с избыточным демпфированием учитывайте продолжительность от 10% до 90% от окончательного значения. Время подъема обозначается через t r .
При t = t 1 = 0, c (t) = 0.
Мы знаем, что окончательное значение шага ответа равно единице.
Следовательно, при $ t = t_2 $ значение шага отклика равно единице. Подставим эти значения в следующее уравнение.
$$ c (t) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta) $$
$$ c (t_2) = 1 = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt_2}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_2 + \ theta) $$
$$ \ Rightarrow \ left (\ frac {e ^ {- \ delta \ omega_nt_2}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_2 + \ theta) = 0 $$
$$ \ Rightarrow \ sin (\ omega_dt_2 + \ theta) = 0 $$
$$ \ Rightarrow \ omega_dt_2 + \ theta = \ pi $$
$$ \ Rightarrow t_2 = \ frac {\ pi- \ theta} {\ omega_d} $$
Подставим значения t 1 и t 2 в следующее уравнение времени нарастания ,
$$ t_r = t_2-t_1 $$
$$ \ Следовательно \: t_r = \ frac {\ pi- \ theta} {\ omega_d} $$
Из приведенного выше уравнения можно сделать вывод, что время нарастания $ t_r $ и затухающая частота $ \ omega_d $ обратно пропорциональны друг другу.
Час пик
Это время, необходимое для ответа, чтобы достичь пикового значения в первый раз. Обозначается $ t_p $. При $ t = t_p $ первый производный ответа равен нулю.
Мы знаем, что пошаговый отклик системы второго порядка для случая недостаточного затухания
$$ c (t) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt + \ theta) $$
Продифференцируйте $ c (t) $ относительно ‘t’.
$$ \ frac {\ text {d} c (t)} {\ text {d} t} = — \ left (\ frac {e ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ right) \ omega_d \ cos (\ omega_dt + \ theta) — \ left (\ frac {- \ delta \ omega_ne ^ {- \ delta \ omega_nt}} {\ sqrt {1- \ delta ^ 2}} \ справа) \ sin (\ omega_dt + \ theta) $$
Замените $ t = t_p $ и $ \ frac {\ text {d} c (t)} {\ text {d} t} = 0 $ в вышеприведенном уравнении.
$$ 0 = — \ left (\ frac {e ^ {- \ delta \ omega_nt_p}} {\ sqrt {1- \ delta ^ 2}} \ right) \ left [\ omega_d \ cos (\ omega_dt_p + \ theta) — \ delta \ omega_n \ sin (\ omega_dt_p + \ theta) \ right] $$
$$ \ Rightarrow \ omega_n \ sqrt {1- \ delta ^ 2} \ cos (\ omega_dt_p + \ theta) — \ delta \ omega_n \ sin (\ omega_dt_p + \ theta) = 0 $$
$$ \ Rightarrow \ sqrt {1- \ delta ^ 2} \ cos (\ omega_dt_p + \ theta) — \ delta \ sin (\ omega_dt_p + \ theta) = 0 $$
$$ \ Rightarrow \ sin (\ theta) \ cos (\ omega_dt_p + \ theta) — \ cos (\ theta) \ sin (\ omega_dt_p + \ theta) = 0 $$
$$ \ Rightarrow \ sin (\ theta- \ omega_dt_p- \ theta) = 0 $$
$$ \ Rightarrow sin (- \ omega_dt_p) = 0 \ Rightarrow — \ sin (\ omega_dt_p) = 0 \ Rightarrow sin (\ omega_dt_p) = 0 $$
$$ \ Rightarrow \ omega_dt_p = \ pi $$
$$ \ Rightarrow t_p = \ frac {\ pi} {\ omega_d} $$
Из приведенного выше уравнения можно сделать вывод, что время пика $ t_p $ и затухающая частота $ \ omega_d $ обратно пропорциональны друг другу.
Пик Overshoot
Пик перерегулирования M p определяется как отклонение отклика в пиковое время от конечного значения отклика. Это также называется максимальным выбросом .
Математически мы можем записать это как
$$ m_p = с (t_p) -c (\ infty) $$
Куда,
c (t p ) — пиковое значение ответа.
c (∞) — окончательное (установившееся) значение ответа.
При $ t = t_p $ ответ c (t) равен —
$$ c (t_p) = 1- \ left (\ frac {e ^ {- \ delta \ omega_nt_p}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin (\ omega_dt_p + \ theta) $$
Замените $ t_p = \ frac {\ pi} {\ omega_d} $ в правой части вышеприведенного уравнения.
$$ c (t_P) = 1- \ left (\ frac {e ^ {- \ delta \ omega_n \ left (\ frac {\ pi} {\ omega_d} \ right)}} {\ sqrt {1- \ delta ^ 2}} \ right) \ sin \ left (\ omega_d \ left (\ frac {\ pi} {\ omega_d} \ right) + \ theta \ right) $$
$$ \ Rightarrow c (t_p) = 1- \ left (\ frac {e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)}} { \ sqrt {1- \ delta ^ 2}} \ right) (- \ sin (\ theta)) $$
Мы знаем это
$$ \ Sin (\ Theta) = \ SQRT {1- \ дельта ^ 2} $$
Итак, мы получим $ c (t_p) $ как
$$ c (t_p) = 1 + e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} $$
Подставьте значения $ c (t_p) $ и $ c (\ infty) $ в уравнение выброса пика.
$$ M_p = 1 + e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} — 1 $$
$$ \ Rightarrow M_p = e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} $$
Процент пикового перерегулирования% $ M_p $ можно рассчитать с помощью этой формулы.
$$ \% M_p = \ frac {M_p} {c (\ infty)} \ times 100 \% $$
Подставляя значения $ M_p $ и $ c (\ infty) $ в приведенную выше формулу, мы получим Процент превышения пика $ \% M_p $ как
$$ \% M_p = \ left (e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} \ right) \ times 100 \% $$
Из приведенного выше уравнения можно сделать вывод, что процент превышения пика $ \% M_p $ уменьшится, если коэффициент демпфирования $ \ delta $ увеличится.
Расчетное время
Это время, необходимое для того, чтобы ответ достиг установившегося состояния и остался в указанных пределах допуска около конечного значения. В общем, допустимые пределы составляют 2% и 5%. Время установления обозначается как $ t_s $.
Время установления для диапазона допуска 5% —
$$ t_s = \ гидроразрыва {3} {\ Delta \ omega_n} = 3 \ тау $$
Время установления для диапазона допуска 2% —
$$ t_s = \ гидроразрыва {4} {\ Delta \ omega_n} = 4 \ тау $$
Где $ \ tau $ — постоянная времени, равная $ \ frac {1} {\ delta \ omega_n} $.
-
И время установления $ t_s $, и постоянная времени $ \ tau $ обратно пропорциональны коэффициенту затухания $ \ delta $.
-
И время установления $ t_s $, и постоянная времени $ \ tau $ не зависят от усиления системы. Это означает, что даже прирост системы меняется, время установления $ t_s $ и постоянная времени $ \ tau $ никогда не изменятся.
И время установления $ t_s $, и постоянная времени $ \ tau $ обратно пропорциональны коэффициенту затухания $ \ delta $.
И время установления $ t_s $, и постоянная времени $ \ tau $ не зависят от усиления системы. Это означает, что даже прирост системы меняется, время установления $ t_s $ и постоянная времени $ \ tau $ никогда не изменятся.
пример
Теперь давайте найдем спецификации временной области системы управления, имеющей передаточную функцию замкнутого контура $ \ frac {4} {s ^ 2 + 2s + 4} $, когда сигнал единичного шага подается в качестве входа в эту систему управления.
Мы знаем, что стандартная форма передаточной функции замкнутой системы управления второго порядка в виде
$$ \ гидроразрыва {\ omega_n ^ 2} {s ^ 2 + 2 \ Delta \ omega_ns + \ omega_n ^ 2} $$
Приравнивая эти две передаточные функции, мы получим естественную частоту $ \ omega_n $ без демпфирования как 2 рад / с и коэффициент демпфирования $ \ delta $ как 0,5.
Мы знаем формулу для затухающей частоты $ \ omega_d $ как
$$ \ omega_d = \ omega_n \ SQRT {1- \ дельта ^ 2} $$
Подставьте значения $ \ omega_n $ и $ \ delta $ в приведенной выше формуле.
$$ \ Rightarrow \ omega_d = 2 \ sqrt {1- (0.5) ^ 2} $$
$$ \ Rightarrow \ omega_d = 1.732 \: рад / с $$
Подставьте значение $ \ delta $ в следующем соотношении
$$ \ Theta = \ соз ^ {- 1} \ Delta $$
$$ \ Rightarrow \ theta = \ cos ^ {- 1} (0.5) = \ frac {\ pi} {3} \: rad $$
Замените вышеуказанные необходимые значения в формуле каждой спецификации временной области и упростите, чтобы получить значения спецификаций временной области для данной передаточной функции.
В следующей таблице приведены формулы спецификаций временной области, подстановка необходимых значений и окончательных значений.
Время задержки
$ T_d = \ гидроразрыва {1 + 0,7 \ дельта} {\ omega_n} $
$ T_d = \ гидроразрыва {1 + 0,7 (0,5)} {2} $
$ t_d $ = 0,675 с
Время нарастания
$ T_r = \ гидроразрыва {\ PI- \ Theta} {\} $ omega_d
$ T_r = \ гидроразрыва {\ р — (\ гидроразрыва {\ Pi} {3})} {1,732} $
$ t_r $ = 1,207 с
Час пик
$ T_p = \ гидроразрыва {\ пи} {\} $ omega_d
$ T_p = \ гидроразрыва {\ пи} {1,732} $
$ t_p $ = 1,813 с
% Peak overshoot
$ \% M_p = \ left (e ^ {- \ left (\ frac {\ delta \ pi} {\ sqrt {1- \ delta ^ 2}} \ right)} \ right) \ times 100 \% $
$ \% M_p = \ left (e ^ {- \ left (\ frac {0.5 \ pi} {\ sqrt {1- (0.5) ^ 2}} \ right)} \ right) \ times 100 \% $
$ \% \: M_p $ = 16,32%
Время установления для диапазона допуска 2%
$ T_s = \ гидроразрыва {4} {\ Delta \ omega_n} $
$ T_S = \ гидроразрыва {4} {(0,5) (2)} $
$ t_s $ = 4 сек