Системы управления — государственная космическая модель

Модель пространства состояний системы линейного инварианта времени (LTI) может быть представлена ​​как

$$\ точка {X} = AX + BU$$

$$Y = CX + DU$$

Первое и второе уравнения известны как уравнение состояния и выходное уравнение соответственно.

Куда,

• X и $\ dot {X}$ — вектор состояния и вектор дифференциального состояния соответственно.

• U и Y — входной вектор и выходной вектор соответственно.

• А — системная матрица.

• B и C — входная и выходная матрицы.

• D — матрица прямой связи.

X и $\ dot {X}$ — вектор состояния и вектор дифференциального состояния соответственно.

U и Y — входной вектор и выходной вектор соответственно.

А — системная матрица.

B и C — входная и выходная матрицы.

D — матрица прямой связи.

Основные понятия государственной космической модели

Следующая основная терминология используется в этой главе.

государственный

Это группа переменных, которая суммирует историю системы, чтобы предсказать будущие значения (результаты).

Государственная переменная

Количество требуемых переменных состояния равно количеству элементов хранения, присутствующих в системе.

Примеры — ток, протекающий через индуктор, напряжение на конденсаторе

Государственный вектор

Это вектор, который содержит переменные состояния в качестве элементов.

В предыдущих главах мы обсудили две математические модели систем управления. Это модель дифференциального уравнения и модель передаточной функции. Модель пространства состояний может быть получена из любой из этих двух математических моделей. Давайте теперь обсудим эти два метода один за другим.

Модель пространства состояний из дифференциального уравнения

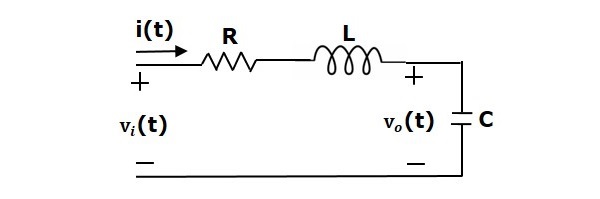
Рассмотрим следующую серию схемы RLC. Он имеет входное напряжение, $v_i (t)$, а ток, протекающий по цепи, составляет $i (t)$.

В этой схеме есть два накопителя (индуктор и конденсатор). Таким образом, число переменных состояния равно двум, и этими переменными состояния являются ток, протекающий через индуктор, $i (t)$ и напряжение на конденсаторе, $v_c (t)$.

Из схемы выходное напряжение $v_0 (t)$ равно напряжению на конденсаторе, $v_c (t)$.

$$v_0 (т) = v_c (т)$$

Примените КВЛ вокруг петли.

$$v_i (т) = Ri (т) + L \ гидроразрыва {\ текст {d} я (т)} {\ текст {d} т} + v_c (т)$$

$$\ Rightarrow \ frac {\ text {d} i (t)} {\ text {d} t} = - \ frac {Ri (t)} {L} - \ frac {v_c (t)} {L} + \ гидроразрыва {v_i (т)} {L}$$

Напряжение на конденсаторе составляет —

$$v_c (t) = \ frac {1} {C} \ int i (t) dt$$

Дифференцируйте вышеприведенное уравнение по времени.

$$\ гидроразрыва {\ текст {d} v_c (т)} {\ текст {d} т} = \ {гидроразрыва я (т)} {C},$$

Вектор состояния, X= beginbmatrixi(t)vc(t) endbmatrix$X = \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix}$

Вектор дифференциального состояния,  dotX= beginbmatrix frac textdi(t) textdt frac textdvc(t) textdt endbmatrix$\ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t )} {\ text {d} t} \ end {bmatrix}$

Мы можем организовать дифференциальные уравнения и выходное уравнение в стандартную форму модели пространства состояний как,

$$\ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t)} { \ text {d} t} \ end {bmatrix} = \ begin {bmatrix} - \ frac {R} {L} & - \ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} + \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix} \ begin {bmatrix } v_i (t) \ end {bmatrix}$$

$$Y = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix}$$

Куда,

$$A = \ begin {bmatrix} - \ frac {R} {L} & - \ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix}, \: B = \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix}, \: C = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \: и \: D = \ begin {bmatrix } 0 \ end {bmatrix}$$

Модель пространства состояний из передаточной функции

Рассмотрим два типа передаточных функций, основанные на типе терминов, присутствующих в числителе.

• Передаточная функция с постоянным членом в Числителе.
• Передаточная функция, имеющая полиномиальную функцию ‘s’ в Числителе.

Передаточная функция с постоянным членом в Числителе

Рассмотрим следующую передаточную функцию системы

$$ \ гидроразрыва {Y (s)} {U (s)} = \ {гидроразрыва b_0} {s ^ п + a_ {п-1} s ^ {п-1} + … + a_1s + A_0} $ $

Переставить приведенное выше уравнение как

$$(s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) Y (s) = b_0 U (s)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} + а_ {п-1} \ гидроразрыва {\ текст {d} ^ {N-1} у (т )} {\ текст {d} т ^ {N-1}} + ... a_1 \ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} + a_0y (т) = B_0 и (т)$$

Позволять

$$у (г) = x_1$$

$$\ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} = x_2 = \ точка {х} -1$$

$$\ гидроразрыва {\ текст {d} ^ 2у (т)} {\ текст {d} т ^ 2} = x_3 = \ точка {х} _2$$

.

.

.

$$ \ гидроразрыва {\ текст {d} ^ {N-1} у (г)} {\ текст {d} т ^ {N-1}} = x_n = \ точки {х} _ {п-1} $ $

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} = \ точка {х} _n$$

и $u (t) = u$

Затем,

$$\ dot {x} _n + a_ {n-1} x_n + ... + a_1x_2 + a_0x_1 = b_0 u$$

Из приведенного выше уравнения мы можем написать следующее уравнение состояния.

$$\ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + b_0 u$$

Выходное уравнение —

$$у (г) = у = x_1$$

Модель пространства состояний —

 dotX= beginbmatrix dotx1 dotx2 vdots dotxn−1 dotxn endbmatrix$\ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix}$

$$= \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\ - a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix}$$

$$Y = \ begin {bmatrix} 1 & 0 & \ dotso & 0 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix}$$

Здесь $D = \ left [0 \ right].$

пример

Найти модель пространства состояний для системы, имеющей передаточную функцию.

$$\ гидроразрыва {Y (ы)} {U (ы)} = \ гидроразрыва {1} {S ^ 2 + S + 1}$$

Переставить, приведенное выше уравнение как,

$$(S ^ 2 + S + 1) Y (s) = U (ы)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$\ гидроразрыва {\ текст {d} ^ 2у (т)} {\ текст {d} т ^ 2} + \ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} + у (т) = U (T)$$

Позволять

$$у (г) = x_1$$

$$\ гидроразрыва {\ текст {d} у (г)} {\ текст {d} т} = x_2 = \ точка {х} -1$$

и $u (t) = u$

Тогда уравнение состояния

$$\ точка {х} _2 = -x_1-x_2 + и$$

Выходное уравнение

$$у (г) = у = x_1$$

Модель пространства состояний

$$\ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} 0 & 1 \\ - 1 & -1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} \ left [u \ right]$$

$$Y = \ begin {bmatrix} 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix}$$

Передаточная функция, имеющая полиномиальную функцию ‘s’ в Числителе

Рассмотрим следующую передаточную функцию системы

$$\ frac {Y (s)} {U (s)} = \ frac {b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0}$$

$$\ Rightarrow \ frac {Y (s)} {U (s)} = \ left (\ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} \ right) (b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0)$$

Вышеупомянутое уравнение имеет вид произведения передаточных функций двух блоков, которые расположены каскадом.

$$\ frac {Y (s)} {U (s)} = \ left (\ frac {V (s)} {U (s)} \ right) \ left (\ frac {Y (s)} {V (s)} \ right)$$

Вот,

$$\ frac {V (s)} {U (s)} = \ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0}$$

Переставить приведенное выше уравнение как

$$(ы ^ п + а_ {п-1} с ^ {N-1} + ... A_0) V (S) = U (ы)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} + а_ {п-1} \ гидроразрыва {\ текст {d} ^ {N-1} v (т )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} v (t)} {\ text {d} t} + a_0v (t) = u (т)$$

Позволять

$$V (T) = x_1$$

$$\ гидроразрыва {\ текст {d} v ((т)} {\ текст {d} т} = x_2 = \ точка {х} -1$$

$$\ гидроразрыва {\ текст {d} ^ 2v (т)} {\ текст {d} т ^ 2} = x_3 = \ точки {х} _2$$

.

.

.

$$ \ гидроразрыва {\ текст {d} ^ {N-1} V (T)} {\ текст {d} т ^ {N-1}} = x_n = \ точка {х} _ {п-1} $ $

$$\ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} = \ точка {х} _n$$

и $u (t) = u$

Тогда уравнение состояния

$$\ точка {х} _n = -a_0x_1-a_1x_2 -...- а_ {п-1} x_n + U$$

Рассматривать,

$$\ гидроразрыва {Y (s)} {V (S)} = b_ns ^ п + B_ {п-1} с ^ {N-1} + ... + b_1s B_0$$

Переставить приведенное выше уравнение как

$$Y (s) = (b_ns ^ п + B_ {п-1} с ^ {N-1} + ... + b_1s B_0) V (S)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$у (г) = b_n \ гидроразрыва {\ текст {d} ^ пу (т)} {\ текст {d} т ^ п} + B_ {п-1} \ гидроразрыва {\ текст {d} ^ {п -1} V (T)} {\ текст {d} т ^ {N-1}} + ... b_1 \ гидроразрыва {\ текст {d} v (т)} {\ текст {d} т} + b_0v (т)$$

Подставляя переменные состояния и $y (t) = y$ в вышеприведенном уравнении, получим выходное уравнение как,

$$у = b_n \ точка {х} _n + b_ {п-1} x_n + ... + b_1x_2 + b_0x_1$$

Замените значение $\ dot {x} _n$ в приведенном выше уравнении.

$$у = b_n (-a_0x_1-a_1x_2 -...- а_ {п-1} x_n + и) + B_ {п-1} x_n + ... + b_1x_2 b_0x_1$$

$$y = (b_0-b_na_0) x_1 + (b_1-b_na_1) x_2 + ... + (b_ {n-1} -b_na_ {n-1}) x_n + b_n u$$

Модель пространства состояний

 dotX= beginbmatrix dotx1 dotx2 vdots dotxn−1 dotxn endbmatrix$\ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ dot {x} _n \ end {bmatrix}$

$$= \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\ - a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix}$$

Y=[b0−bna0 quadb1−bna1 quad... quadbn−2−bnan−2 quadbn−1−bnan−1] beginbmatrixx1x2 vdotsxn−1xn endbmatrix $$Y = [b_0-b_na_0 \ quad b_1-b_na_1 \ quad ... \ quad b_ {n-2} -b_na_ {n-2} \ quad b_ {n-1} -b_na_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix}$$

Если $b_n = 0$, то

Y=[b0 quadb1 quad... quadbn−2 quadbn−1] beginbmatrixx1x2 vdotsxn−1xn endbmatrix $$Y = [b_0 \ quad b_1 \ quad ... \ quad b_ {n-2} \ quad b_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n- 1} \\ x_n \ end {bmatrix}$$