Стабильность является важной концепцией. В этой главе давайте обсудим стабильность системы и типы систем, основанных на устойчивости.
Что такое стабильность?
Система называется стабильной, если ее выход находится под контролем. В противном случае он называется нестабильным. Стабильная система производит ограниченный вывод для данного ограниченного ввода.
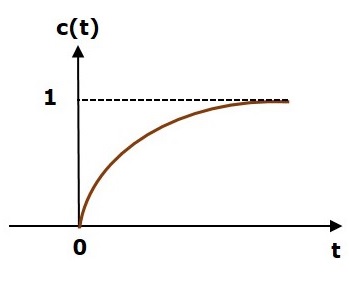
На следующем рисунке показан ответ стабильной системы.
Это ответ системы управления первого порядка на шаговый ввод. Этот ответ имеет значения между 0 и 1. Таким образом, это ограниченный вывод. Мы знаем, что сигнал единичного шага имеет значение один для всех положительных значений t, включая ноль. Итак, это ограниченный ввод. Следовательно, система управления первого порядка стабильна, так как и вход, и выход ограничены.
Типы систем на основе стабильности
Мы можем классифицировать системы на основе стабильности следующим образом.
- Абсолютно стабильная система
- Условно стабильная система
- Маргинально стабильная система
Абсолютно стабильная система
Если система стабильна для всего диапазона значений системных компонентов, то она известна как абсолютно стабильная система . Система управления с разомкнутым контуром абсолютно устойчива, если все полюсы передаточной функции с разомкнутым контуром присутствуют в левой половине плоскости ‘s’ . Аналогично, система управления с обратной связью является абсолютно устойчивой, если все полюсы передаточной функции с обратной связью присутствуют в левой половине плоскости ‘s’.
Условно Стабильная Система
Если система стабильна для определенного диапазона значений компонентов системы, то она называется условно стабильной системой .
Стабильно стабильная система
Если система стабильна, создавая выходной сигнал с постоянной амплитудой и постоянной частотой колебаний для ограниченного входа, то она известна как предельно стабильная система . Система управления с разомкнутым контуром является минимально устойчивой, если на мнимой оси присутствуют любые два полюса передаточной функции с разомкнутым контуром. Аналогично, система управления с обратной связью является минимально устойчивой, если на мнимой оси присутствуют любые два полюса передаточной функции с обратной связью.