Системы управления — ошибки стационарного состояния

Отклонение выхода системы управления от требуемого отклика в установившемся режиме называется ошибкой установившегося состояния . Он представлен как $e_ {ss}$. Мы можем найти ошибку стационарного состояния, используя теорему об окончательном значении, следующим образом.

$$e_ {ss} = \ lim_ {t \ to \ infty} e (t) = \ lim_ {s \ to 0} sE (s)$$

Куда,

E (s) — преобразование Лапласа сигнала ошибки, $e (t)$

Давайте обсудим, как находить ошибки установившегося состояния для систем управления с единой обратной связью и не единой обратной связи.

Ошибки установившегося состояния для систем обратной связи Unity

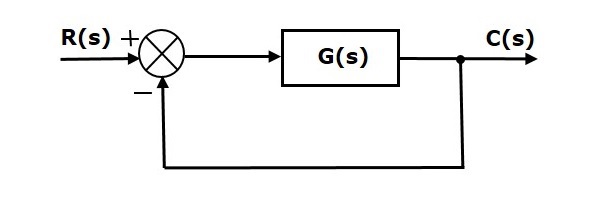
Рассмотрим следующую блок-схему замкнутой системы управления, которая имеет единую отрицательную обратную связь.

Куда,

• R (s) — преобразование Лапласа эталонного входного сигнала $r (t)$
• C (s) — преобразование Лапласа выходного сигнала $c (t)$

Мы знаем передаточную функцию замкнутой системы управления с отрицательной обратной связью как

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {G (s)} {1 + G (s)}$$

$$\ Rightarrow C (s) = \ frac {R (s) G (s)} {1 + G (s)}$$

Выход точки суммирования —

$$Е (с) = R (S) -C (ы)$$

Замените значение $C (s)$ в приведенном выше уравнении.

$$Е (ы) = R (S) - \ гидроразрыва {R (S) G (s)} {1 + G (s)}$$

$$\ Rightarrow E (s) = \ frac {R (s) + R (s) G (s) -R (s) G (s)} {1 + G (s)}$$

$$\ Rightarrow E (s) = \ frac {R (s)} {1 + G (s)}$$

Подставьте значение $E (s)$ в формулу ошибки стационарного состояния

$$e_ {ss} = \ lim_ {s \ to 0} \ frac {sR (s)} {1 + G (s)}$$

В следующей таблице показаны ошибки стационарного состояния и константы ошибок для стандартных входных сигналов, таких как шаг единицы измерения, линейное изменение скорости и единичные параболические сигналы.

единичный шаговой сигнал

$\ Гидроразрыва {1} {1 + k_p}$

$K_p = \ lim_ {s \ to 0} G (s)$

сигнал рампы

$\ Гидроразрыва {1} {K_v}$

$K_v = \ lim_ {s \ to 0} сГ (с)$

единичный параболический сигнал

$\ Гидроразрыва {1} {K_a}$

$K_a = \ lim_ {s \ to 0} с ^ 2G (s)$

Где $K_p$, $K_v$ и $K_a$ — постоянная ошибки положения, постоянная ошибки скорости и постоянная ошибки ускорения соответственно.

Примечание. Если какой-либо из указанных выше входных сигналов имеет амплитуду, отличную от единицы, умножьте соответствующую ошибку установившегося состояния на эту амплитуду.

Примечание. Мы не можем определить ошибку установившегося состояния для импульсного сигнала устройства, поскольку он существует только в начале координат. Таким образом, мы не можем сравнивать импульсную характеристику с единичным импульсным входом, поскольку t обозначает бесконечность.

пример

Найдем ошибку установившегося состояния для входного сигнала $r (t) = \ left (5 + 2t + \ frac {t ^ 2} {2} \ right) u (t)$ единой системы управления отрицательной обратной связью с $G (с) = \ гидроразрыва {(5 + 4)} {s ^ 2 (s + 1) (s + 20)}$

Данный входной сигнал представляет собой комбинацию трех сигналов: ступенчатого, линейного и параболического. В следующей таблице приведены константы ошибок и значения ошибок установившегося состояния для этих трех сигналов.

$R_1 (т) = 5U (т)$

$K_p = \ lim_ {s \ to 0} G (s) = \ infty$

$E_ {SS1} = \ гидроразрыва {5} {1 + k_p} = 0$

$R_2 (т) = 2tu (т)$

$K_v = \ lim_ {s \ to 0} сГ (с) = \ infty$

{$E_ ss2} = \ гидроразрыва {2} {K_v} = 0$

$R_3 (т) = \ гидроразрыва {т ^ 2} {2} и (т)$

$K_a = \ lim_ {s \ to 0} с ^ 2G (s) = 1$

$E_ {ss3} = \ гидроразрыва {1} {k_a} = 1$

Мы получим общую ошибку установившегося состояния, добавив три вышеуказанные ошибки установившегося состояния.

$$E_ {сс} = {е_ SS1} + е- {SS2} + е- {SS3}$$

$$\ Rightarrow e_ {ss} = 0 + 0 + 1 = 1$$

Таким образом, мы получили ошибку стационарного состояния $e_ {ss}$ как 1 для этого примера.

Ошибки установившегося состояния для систем с неединичной обратной связью

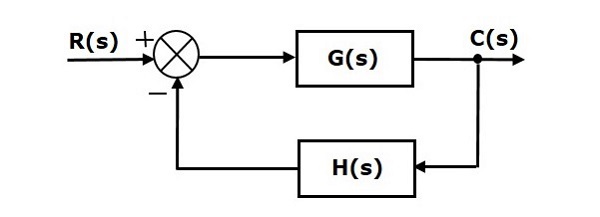
Рассмотрим следующую блок-схему замкнутой системы управления с отрицательной обратной связью.

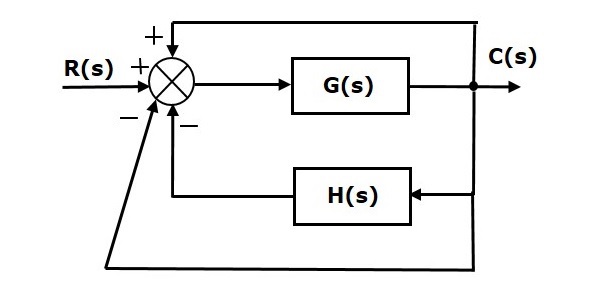
Мы можем найти ошибки стационарного состояния только для систем с обратной связью. Таким образом, мы должны преобразовать систему неединой обратной связи в единую систему обратной связи. Для этого включите один единый путь положительной обратной связи и один единственный путь отрицательной обратной связи в приведенную выше блок-схему. Новая блок-схема выглядит так, как показано ниже.

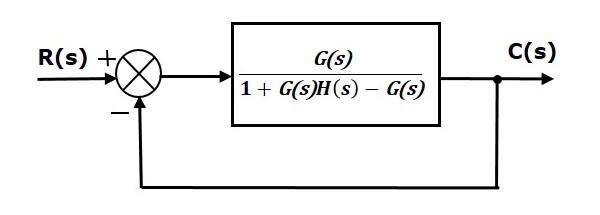
Упростите приведенную выше блок-схему, сохранив единую отрицательную обратную связь как есть. Ниже приведена упрощенная блок-схема.

Эта блок-схема напоминает блок-схему единой системы управления с обратной связью с обратной связью. Здесь единственный блок имеет передаточную функцию $\ frac {G (s)} {1 + G (s) H (s) -G (s)}$ вместо $G (s)$. Теперь вы можете рассчитать ошибки установившегося состояния, используя формулу ошибки установившегося состояния, приведенную для систем единой отрицательной обратной связи.

Примечание. Бессмысленно находить ошибки стационарного состояния для неустойчивых систем с замкнутым контуром. Таким образом, мы должны вычислять ошибки стационарного состояния только для замкнутых систем. Это означает, что мы должны проверить, является ли система управления стабильной или нет, прежде чем обнаруживать ошибки установившегося состояния. В следующей главе мы обсудим концептуальную стабильность.