Ответ системы первого заказа

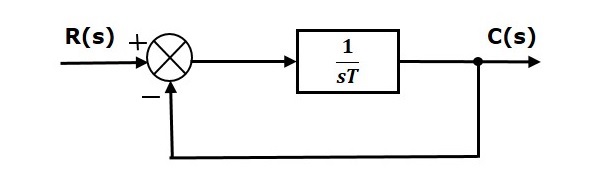
В этой главе давайте обсудим временную характеристику системы первого порядка. Рассмотрим следующую блок-схему замкнутой системы управления. Здесь передаточная функция без обратной связи $\ frac {1} {sT}$ связана с единственной отрицательной обратной связью.

Мы знаем, что передаточная функция замкнутой системы управления имеет единую отрицательную обратную связь, как,

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {G (s)} {1 + G (s)}$$

Замените $G (s) = \ frac {1} {sT}$ в приведенном выше уравнении.

$$\ гидроразрыва {C (S)} {R (S)} = \ гидроразрыва {\ гидроразрыва {1} {St}} {1+ \ гидроразрыва {1} {St}} = \ гидроразрыва {1} {ST + 1}$$

Степень s равна единице в знаменателе. Следовательно, вышеупомянутая передаточная функция имеет первый порядок, и система называется системой первого порядка .

Мы можем переписать приведенное выше уравнение как

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$$

Куда,

• C (s) — преобразование Лапласа выходного сигнала c (t),

• R (s) — преобразование Лапласа входного сигнала r (t), и

• Т — постоянная времени.

C (s) — преобразование Лапласа выходного сигнала c (t),

R (s) — преобразование Лапласа входного сигнала r (t), и

Т — постоянная времени.

Выполните следующие действия, чтобы получить ответ (вывод) системы первого порядка во временной области.

• Возьмем преобразование Лапласа входного сигнала $r (t)$.

• Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

• Замените значение $R (s)$ в приведенном выше уравнении.

• Делайте частичные дроби $C (s)$, если требуется.

• Примените обратное преобразование Лапласа к $C (s)$.

Возьмем преобразование Лапласа входного сигнала $r (t)$.

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените значение $R (s)$ в приведенном выше уравнении.

Делайте частичные дроби $C (s)$, если требуется.

Примените обратное преобразование Лапласа к $C (s)$.

В предыдущей главе мы видели стандартные тестовые сигналы, такие как импульс, шаг, линейное изменение и параболический сигнал. Давайте теперь выясним ответы системы первого порядка для каждого входа, один за другим. Имя ответа дается в соответствии с именем входного сигнала. Например, отклик системы на импульсный вход называется импульсным откликом.

Импульсный отклик системы первого порядка

Рассмотрим импульсный сигнал устройства как вход в систему первого порядка.

Итак, $r (t) = \ delta (t)$

Примените преобразование Лапласа с обеих сторон.

$R (s) = 1$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = 1$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) (1) = \ frac {1} {sT + 1}$$

Переставьте приведенное выше уравнение в одну из стандартных форм преобразований Лапласа.

$$C (s) = \ frac {1} {T \ left (\ s + \ frac {1} {T} \ right)} \ Rightarrow C (s) = \ frac {1} {T} \ left (\ frac {1} {s + \ frac {1} {T}} \ right)$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ frac {1} {T} e ^ \ left ({- \ frac {t} {T}} \ right) u (t)$$

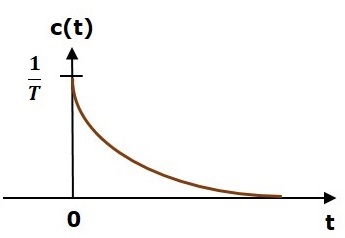
Импульсная характеристика устройства показана на следующем рисунке.

Единичная импульсная характеристика , c (t), представляет собой экспоненциальный затухающий сигнал для положительных значений «t», и он равен нулю для отрицательных значений «t».

Шаговая реакция системы первого заказа

Рассмотрим сигнал единичного шага как вход в систему первого порядка.

Итак, $r (t) = u (t)$

Примените преобразование Лапласа с обеих сторон.

$$R (s) = \ гидроразрыва {1} {s}$$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = \ frac {1} {s}$ в приведенном выше уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s} \ right) = \ frac {1} {s \ left (sT + 1 \ right)}$$

Делаем частичные дроби из C (s).

$$C (s) = \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1}$$

$$\ Rightarrow \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A \ left (sT + 1 \ right) + Bs} {s \ left (sT + 1 \ right)}$$

Обе стороны знаменателя одинаковы. Таким образом, они будут отменены друг другом. Следовательно, приравнивайте члены числителя.

$$1 = A \ left (sT + 1 \ right) + Bs$$

Приравнивая постоянные члены с обеих сторон, вы получите A = 1.

Подставим A = 1 и уравняем коэффициент слагаемых с обеих сторон.

$$0 = T + B \ Rightarrow B = -T$$

Подставим, A = 1 и B = −T при частичном разложении в $C (s)$.

$$C (s) = \ frac {1} {s} - \ frac {T} {sT + 1} = \ frac {1} {s} - \ frac {T} {T \ left (s + \ frac { 1} {T} \ right)}$$

$$\ Rightarrow C (s) = \ frac {1} {s} - \ frac {1} {s + \ frac {1} {T}}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (1-e ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t)$$

Реакция на единичный шаг c (t) имеет как переходные, так и установившиеся состояния.

Переходный член в ответе на единичный шаг —

$$c_ {tr} (t) = - e ^ {- \ left (\ frac {t} {T} \ right)} u (t)$$

Термин установившегося состояния в ответе шага блока —

$$C_ {сс} (т) = и (т)$$

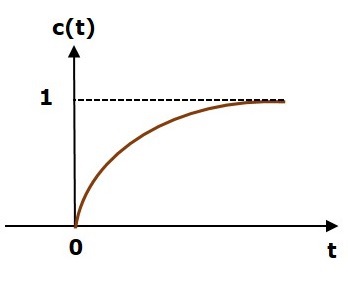
На следующем рисунке показан ответ шага устройства.

Значение единичного шага отклика c (t) равно нулю при t = 0 и для всех отрицательных значений t. Он постепенно увеличивается от нулевого значения и, наконец, достигает единицы в устойчивом состоянии. Таким образом, значение установившегося состояния зависит от величины входного сигнала.

Реакция системы первого порядка

Рассмотрим сигнал линейного изменения в качестве входа в систему первого порядка.

$Итак, r (t) = tu (t)$

Примените преобразование Лапласа с обеих сторон.

$$R (s) = \ гидроразрыва {1} {s ^ 2}$$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = \ frac {1} {s ^ 2}$ в вышеприведенном уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 2} \ right) = \ frac {1} {s ^ 2 ( ST + 1)}$$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {1} {s ^ 2 (ST + 1)} = \ гидроразрыва {A}, {s ^ 2} + \ гидроразрыва {B}, {s} + \ гидроразрыва {C}, {St +1}$$

$$\ Rightarrow \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A (sT + 1) + Bs (sT + 1) + Cs ^ 2} {s ^ 2 (sT + 1) }$$

Обе стороны знаменателя одинаковы. Таким образом, они будут отменены друг другом. Следовательно, приравнивайте члены числителя.

$$1 = А (St + 1) Bs (ST + 1) + Cs ^ 2$$

Приравнивая постоянные члены с обеих сторон, вы получите A = 1.

Подставим A = 1 и уравняем коэффициент слагаемых с обеих сторон.

$$0 = T + B \ Rightarrow B = -T$$

Аналогично подставьте B = −T и приравните коэффициент слагаемых $s ^ 2$ с обеих сторон. Вы получите $C = T ^ 2$.

Замените A = 1, B = −T и $C = T ^ 2$ в разложении по частям в $C (s)$.

$$C (S) = \ гидроразрыва {1} {s ^ 2} - \ гидроразрыва {T}, {s} + \ гидроразрыва {Т ^ 2} {ST + 1} = \ гидроразрыва {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {T \ left (s + \ frac {1} {T} \ right)}$$

$$\ Rightarrow C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}}$$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (t-T + Te ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t)$$

Реакция единичного изменения , c (t), имеет как переходные, так и установившиеся состояния.

Переходный член в отклике линейного изменения —

$$c_ {tr} (t) = Te ^ {- \ left (\ frac {t} {T} \ right)} u (t)$$

Термин установившегося состояния в ответе линейного изменения —

$$C_ {сс} (т) = (Tt) и (г)$$

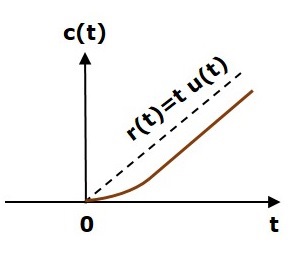
На следующем рисунке показан ответ линейного изменения.

Реакция единичного изменения , c (t), следует за входным сигналом линейного изменения для всех положительных значений t. Но есть отклонение T единиц от входного сигнала.

Параболический ответ системы первого порядка

Рассмотрим единичный параболический сигнал как вход в систему первого порядка.

Итак, $r (t) = \ frac {t ^ 2} {2} u (t)$

Примените преобразование Лапласа с обеих сторон.

$$R (s) = \ гидроразрыва {1} {s ^ 3}$$

Рассмотрим уравнение, $C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s)$

Замените $R (s) = \ frac {1} {s ^ 3}$ в вышеприведенном уравнении.

$$C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 3} \ right) = \ frac {1} {s ^ 3 ( ST + 1)}$$

Делаем частичные дроби $C (s)$.

$$C (S) = \ гидроразрыва {1} {s ^ 3 (ST + 1)} = \ гидроразрыва {A}, {s ^ 3} + \ гидроразрыва {B}, {s ^ 2} + \ гидроразрыва {C} {s} + \ гидроразрыва {D} {ST + 1}$$

После упрощения вы получите значения A, B, C и D как 1, −T,T2и−T3$-T, \: T ^ 2 \: и \: −T ^ 3$ соответственно. Подставьте эти значения в приведенное выше частичное расширение доли C (s).

C(S)= гидроразрыва1s3− гидроразрываT,s2+ гидроразрываТ2s− гидроразрываТ3ST+1 RightarrowC(s)= frac1s3− fracTs2+ fracT2s− fracT2s+ гидроразрыва1T$C (S) = \ гидроразрыва {1} {s ^ 3} - \ гидроразрыва {T}, {s ^ 2} + \ гидроразрыва {Т ^ 2} {s} - \ гидроразрыва {Т ^ 3} {ST + 1 } \: \ Rightarrow C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 2} {s + \ гидроразрыва {1} {T}}$

Примените обратное преобразование Лапласа с обеих сторон.

$$c (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} \ right ) и (г)$$

Единичный параболический отклик c (t) имеет как переходные, так и стационарные условия.

Переходный член в единичном параболическом ответе

$$C_ {tr} (t) = - T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} u (t)$$

Член стационарного состояния в единичном параболическом ответе равен

$$C_ {ss} (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2 \ right) u (t)$$

Из этих ответов мы можем сделать вывод, что системы управления первого порядка нестабильны с линейными и параболическими входами, потому что эти реакции продолжают увеличиваться даже в бесконечное количество времени. Системы управления первого порядка стабильны с импульсными и шаговыми входами, потому что эти отклики имеют ограниченный выход. Но импульсный отклик не имеет устойчивого состояния. Таким образом, шаговый сигнал широко используется во временной области для анализа систем управления по их откликам.