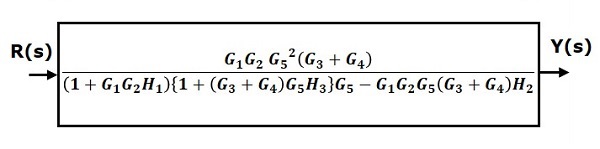Концепции, обсуждаемые в предыдущей главе, полезны для сокращения (упрощения) блок-схем.
Правила сокращения блок-схем
Следуйте этим правилам для упрощения (уменьшения) блок-схемы, которая состоит из множества блоков, точек суммирования и точек взлета.
-
Правило 1 — Проверьте блоки, соединенные последовательно и упростите.
-
Правило 2 — Проверьте блоки, соединенные параллельно, и упростите.
-
Правило 3 — Проверьте блоки, подключенные в петле обратной связи, и упростите.
-
Правило 4 — Если есть трудности с точкой взлета при упрощении, сдвиньте ее вправо.
-
Правило 5 — Если есть трудности с суммированием точки при упрощении, сдвиньте ее влево.
-
Правило 6 — Повторяйте вышеуказанные шаги, пока не получите упрощенную форму, то есть один блок.
Правило 1 — Проверьте блоки, соединенные последовательно и упростите.
Правило 2 — Проверьте блоки, соединенные параллельно, и упростите.
Правило 3 — Проверьте блоки, подключенные в петле обратной связи, и упростите.
Правило 4 — Если есть трудности с точкой взлета при упрощении, сдвиньте ее вправо.
Правило 5 — Если есть трудности с суммированием точки при упрощении, сдвиньте ее влево.
Правило 6 — Повторяйте вышеуказанные шаги, пока не получите упрощенную форму, то есть один блок.
Примечание . Передаточная функция, присутствующая в этом отдельном блоке, является передаточной функцией всей блок-схемы.
пример
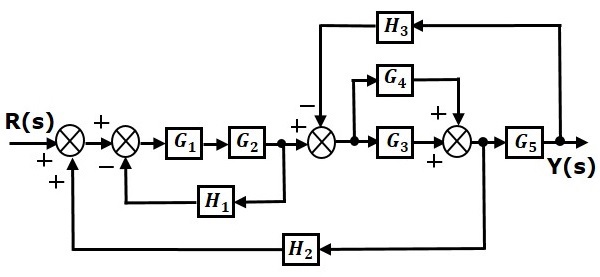
Рассмотрим блок-схему, показанную на следующем рисунке. Давайте упростим (уменьшим) эту блок-схему, используя правила сокращения блок-схем.
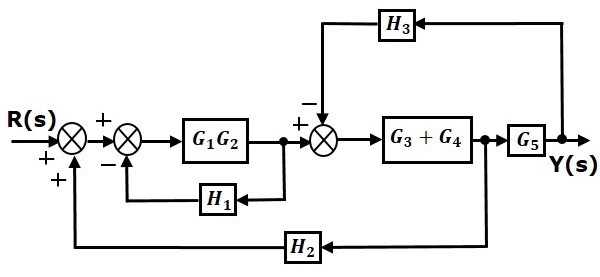
Шаг 1 — Используйте правило 1 для блоков $ G_1 $ и $ G_2 $. Используйте правило 2 для блоков $ G_3 $ и $ G_4 $. Модифицированная блок-схема показана на следующем рисунке.
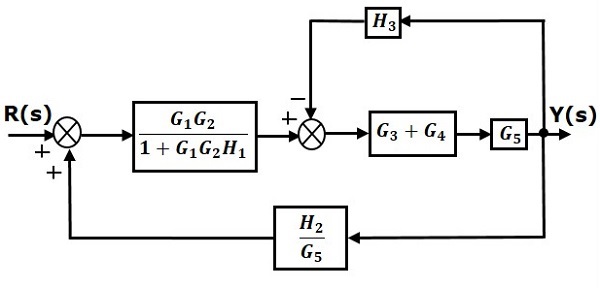
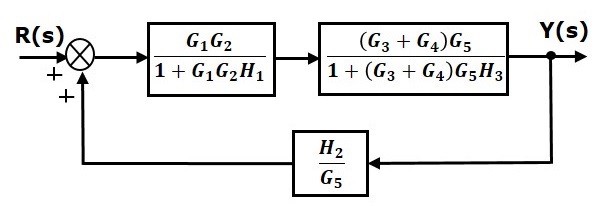
Шаг 2 — Используйте правило 3 для блоков $ G_1G_2 $ и $ H_1 $. Используйте Правило 4 для смещения точки взлета после блока $ G_5 $. Модифицированная блок-схема показана на следующем рисунке.
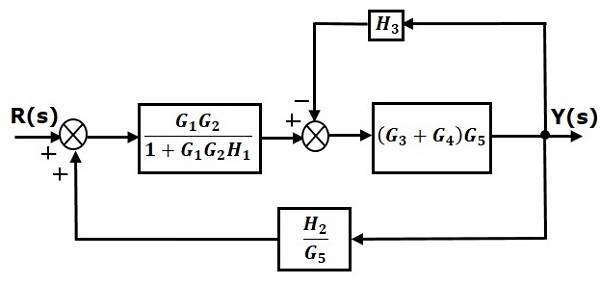
Шаг 3 — Используйте правило 1 для блоков $ (G_3 + G_4) $ и $ G_5 $. Модифицированная блок-схема показана на следующем рисунке.
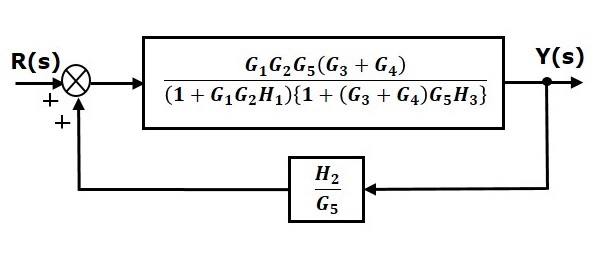
Шаг 4 — Используйте правило 3 для блоков $ (G_3 + G_4) G_5 $ и $ H_3 $. Модифицированная блок-схема показана на следующем рисунке.
Шаг 5 — Используйте Правило 1 для блоков, соединенных последовательно. Модифицированная блок-схема показана на следующем рисунке.
Шаг 6 — Используйте правило 3 для блоков, подключенных в петле обратной связи. Модифицированная блок-схема показана на следующем рисунке. Это упрощенная блок-схема.
Следовательно, передаточная функция системы
$$ \ frac {Y (s)} {R (s)} = \ frac {G_1G_2G_5 ^ 2 (G_3 + G_4)} {(1 + G_1G_2H_1) \ lbrace 1+ (G_3 + G_4) G_5H_3 \ rbrace G_5-G_1G_2G_5 (G_3 + G_4) H_2} $$
Примечание. Выполните следующие действия, чтобы рассчитать передаточную функцию блок-схемы, имеющей несколько входов.
-
Шаг 1 — Найти передаточную функцию блок-схемы, рассматривая по одному входу за раз, а оставшиеся входы сделать равными нулю.
-
Шаг 2 — Повторите шаг 1 для оставшихся входов.
-
Шаг 3 — Получить общую функцию передачи, добавив все эти функции передачи.
Шаг 1 — Найти передаточную функцию блок-схемы, рассматривая по одному входу за раз, а оставшиеся входы сделать равными нулю.
Шаг 2 — Повторите шаг 1 для оставшихся входов.
Шаг 3 — Получить общую функцию передачи, добавив все эти функции передачи.
Процесс сокращения структурной схемы занимает больше времени для сложных систем. Потому что мы должны нарисовать (частично упрощенную) блок-схему после каждого шага. Итак, чтобы преодолеть этот недостаток, используйте графики потока сигналов (представление).
В следующих двух главах мы обсудим концепции, связанные с графиками потока сигналов, т. Е. Как представить график потока сигналов из заданной блок-схемы и вычислить передаточную функцию, просто используя формулу усиления без выполнения какого-либо процесса сокращения.