Mason’s Gain Formula

Давайте теперь обсудим формулу усиления Мэйсона. Предположим, что в графе потока сигналов есть «N» прямых путей. Усиление между входными и выходными узлами графа потока сигналов является ничем иным, как передаточной функцией системы. Его можно рассчитать по формуле усиления Мейсона.

Формула усиления Мэйсона

$$T = \ frac {C (s)} {R (s)} = \ frac {\ Sigma ^ N _ {i = 1} P_i \ Delta _i} {\ Delta}$$

Куда,

• C (s) — выходной узел

• R (s) — входной узел

• T — передаточная функция или усиление между $R (s)$ и $C (s)$.

• P _i — это i- ^й коэффициент усиления прямого пути

C (s) — выходной узел

R (s) — входной узел

T — передаточная функция или усиление между $R (s)$ и $C (s)$.

P _i — это i- ^й коэффициент усиления прямого пути

 Delta=1−(суммаизвсеотдельныйциклвыигрыш)$\ Delta = 1- (сумма \: из \: все \: отдельный \: цикл \: выигрыш)$

+(суммаofgainproductsofallвозможноtwonontouchingloops)$+ (сумма \: of \: gain \: products \: of \: all \: возможно \: two \: nontouching \: loops)$

−(суммаofgainproductsofallвозможнотринеприкосновениециклы)+... $$- (сумма \: of \: gain \: products \: of \: all \: возможно \: три \: неприкосновение \: циклы) + ...$$

Δ _i получается из Δ путем удаления петель, которые касаются i- ^го прямого пути .

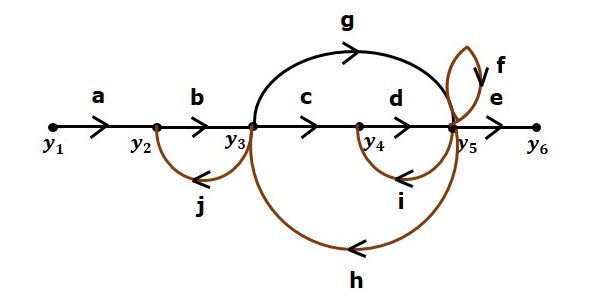
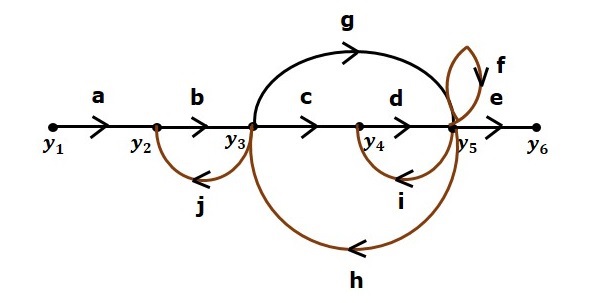
Рассмотрим следующий график потока сигналов, чтобы понять основную терминологию, используемую здесь.

Дорожка

Это обход ветвей от одного узла к любому другому узлу в направлении стрелок ветвления. Он не должен проходить через какой-либо узел более одного раза.

Примеры — $y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5$ и $y_5 \ rightarrow y_3 \ rightarrow y_2$

Прямой путь

Путь, который существует от входного узла до выходного узла, известен как прямой путь .

Примеры — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$ и $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

Прямой путь

Это получается путем вычисления произведения всех ветвей усиления прямого пути.

Примеры — $abcde$ — усиление прямого пути для $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$, а abge — усиление прямого пути $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

петля

Путь, который начинается с одного узла и заканчивается в том же узле, называется циклом . Следовательно, это закрытый путь.

Примеры — $y_2 \ rightarrow y_3 \ rightarrow y_2$ и $y_3 \ rightarrow y_5 \ rightarrow y_3$.

Loop Gain

Это получается путем вычисления произведения всех ветвей усиления цикла.

Примеры — $b_j$ — это усиление цикла для $y_2 \ rightarrow y_3 \ rightarrow y_2$, а $g_h$ — это усиление цикла для $y_3 \ rightarrow y_5 \ rightarrow y_3$.

Бесконтактные петли

Это петли, которые не должны иметь общего узла.

Примеры . Циклы, $y_2 \ rightarrow y_3 \ rightarrow y_2$ и $y_4 \ rightarrow y_5 \ rightarrow y_4$, не затрагиваются.

Расчет передаточной функции по формуле усиления Мэйсона

Рассмотрим тот же график потока сигналов для нахождения передаточной функции.

• Количество прямых путей, N = 2.

• Первый прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$.

• Первое усиление прямого пути, $p_1 = abcde$.

• Второй прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

• Второй прямой путь усиления, $p_2 = abge$.

• Количество отдельных петель, L = 5.

• Циклы — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_3 \ rightarrow y_5 \ rightarrow y_3$, $y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_3$, $y_4 \ rightarrow y_5 \ rightarrow y_4$ и $yar_5$ y_5 $.

• Усиление контура — $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ и $l_5 = f$.

• Количество двух не соприкасающихся петель = 2.

• Первая пара неприкасающих циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_4 \ rightarrow y_5 \ rightarrow y_4$.

• Произведение усиления первой пары неприкосновенных циклов, $l_1l_4 = bjdi$

• Вторая пара неприкосновенных циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_5 \ rightarrow y_5$.

• Произведение усиления второй пары неприкосновенных циклов — $l_1l_5 = bjf$

Количество прямых путей, N = 2.

Первый прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_6$.

Первое усиление прямого пути, $p_1 = abcde$.

Второй прямой путь — $y_1 \ rightarrow y_2 \ rightarrow y_3 \ rightarrow y_5 \ rightarrow y_6$.

Второй прямой путь усиления, $p_2 = abge$.

Количество отдельных петель, L = 5.

Циклы — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_3 \ rightarrow y_5 \ rightarrow y_3$, $y_3 \ rightarrow y_4 \ rightarrow y_5 \ rightarrow y_3$, $y_4 \ rightarrow y_5 \ rightarrow y_4$ и $yar_5$ y_5 $.

Усиление контура — $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ и $l_5 = f$.

Количество двух не соприкасающихся петель = 2.

Первая пара неприкасающих циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_4 \ rightarrow y_5 \ rightarrow y_4$.

Произведение усиления первой пары неприкосновенных циклов, $l_1l_4 = bjdi$

Вторая пара неприкосновенных циклов — $y_2 \ rightarrow y_3 \ rightarrow y_2$, $y_5 \ rightarrow y_5$.

Произведение усиления второй пары неприкосновенных циклов — $l_1l_5 = bjf$

Большее количество (более двух) не соприкасающихся петель не присутствует в этом графике потока сигналов.

Мы знаем,

 Delta=1−(суммаизвсеотдельныйциклвыигрыш)$\ Delta = 1- (сумма \: из \: все \: отдельный \: цикл \: выигрыш)$

+(суммаofgainproductsofallвозможноtwonontouchingloops)$+ (сумма \: of \: gain \: products \: of \: all \: возможно \: two \: nontouching \: loops)$

−(суммаofgainproductsofallвозможнотринеприкосновениециклы)+... $$- (сумма \: of \: gain \: products \: of \: all \: возможно \: три \: неприкосновение \: циклы) + ...$$

Подставим значения в приведенное выше уравнение,

$\ Delta = 1- (bj + gh + cdh + di + f) + (bjdi + bjf) - (0)$

$\ Rightarrow \ Delta = 1- (BJ + GH + CDH + D + F) + BJDI + BJF$

Нет петли, которая не касается первого прямого пути.

Итак, $\ Delta_1 = 1$.

Аналогично, $\ Delta_2 = 1$. Так как нет петли, которая не касается второго прямого пути.

Заменить, N = 2 в формуле усиления Мейсона

$$T = \ frac {C (s)} {R (s)} = \ frac {\ Sigma ^ 2 _ {i = 1} P_i \ Delta _i} {\ Delta}$$

$$Т = \ гидроразрыва {C (S)} {R (S)} = \ {гидроразрыва P_1 \ Delta_1 + P_2 \ Delta_2} {\ Delta}$$

Подставьте все необходимые значения в приведенное выше уравнение.

$$Т = \ гидроразрыва {C (S)} {R (S)} = \ {гидроразрыва (ABCDE) 1+ (abge) 1} {1- (Ь + GH + CDH + ди + ж) + bjdi + BJF }$$

$$\ Rightarrow T = \ frac {C (s)} {R (s)} = \ frac {(abcde) + (abge)} {1- (bj + gh + cdh + di + f) + bjdi + bjf }$$

Следовательно, передаточная функция —

$$ Т = \ гидроразрыва {C (S)} {R (S)} = \ {гидроразрыва (ABCDE) + (abge)} {1- (Ь + GH + CDH + ди + ж) + bjdi + BJF} $ $