Теория сети — топология сети

Топология сети — это графическое представление электрических цепей. Это полезно для анализа сложных электрических цепей путем преобразования их в сетевые графы. Топология сети также называется теорией графов .

Основная терминология топологии сети

Теперь давайте поговорим об основной терминологии этой топологии сети.

график

Сетевой граф просто называется графом . Он состоит из набора узлов, соединенных ветвями. В графах узел является общей точкой двух или более ветвей. Иногда только одна ветвь может подключаться к узлу. Ветвь — это отрезок, соединяющий два узла.

Любую электрическую цепь или сеть можно преобразовать в ее эквивалентный график , заменив пассивные элементы и источники напряжения короткими замыканиями, а источники тока — разомкнутыми. Это означает, что линейные сегменты на графике представляют ветви, соответствующие либо пассивным элементам, либо источникам напряжения электрической цепи.

пример

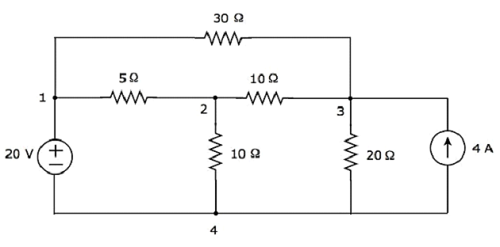
Рассмотрим следующую электрическую цепь .

В вышеупомянутой схеме есть четыре главных узла, и те отмечены как 1, 2, 3 и 4. В вышеупомянутой схеме есть семь ветвей , среди которых одна ветвь содержит источник напряжения 20 В, другая ветвь содержит 4 А Источник тока и остальные пять ответвлений содержат резисторы с сопротивлениями 30 Ом, 5 Ом, 10 Ом, 10 Ом и 20 Ом соответственно.

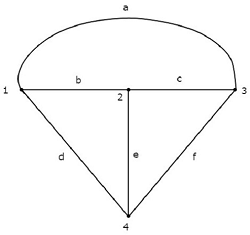
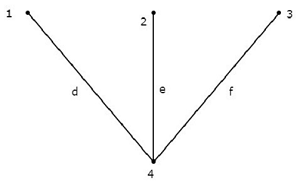
Эквивалентный график, соответствующий вышеуказанной электрической цепи, показан на следующем рисунке.

На приведенном выше графике есть четыре узла, и они помечены 1, 2, 3 и 4 соответственно. Они такие же, как у основных узлов в электрической цепи. На приведенном выше графике есть шесть ветвей, которые помечены как a, b, c, d, e & f соответственно.

В этом случае на графике мы получили на одну ветвь меньше, потому что источник тока 4 А выполнен в виде разомкнутой цепи, при этом преобразовывая электрическую цепь в эквивалентный график.

Из этого примера мы можем сделать следующие выводы:

• Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.

• Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.

Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.

Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.

Типы графиков

Ниже приведены типы графиков —

• Связанный график
• Неподключенный график
• Направленный граф
• Ненаправленный граф

Теперь давайте обсудим эти графики один за другим.

Связанный график

Если существует хотя бы одна ветвь между любыми двумя узлами графа, то она называется связным графом . Это означает, что каждый узел в связанном графе будет иметь одну или несколько ветвей, которые связаны с ним. Таким образом, ни один узел не будет представлен как изолированный или разделенный.

График, показанный в предыдущем примере, является связным графом . Здесь все узлы связаны тремя ветвями.

Неподключенный график

Если в графе существует хотя бы один узел, который не связан даже одной ветвью, то он называется несвязанным графом . Таким образом, в несвязном графе будет один или несколько изолированных узлов.

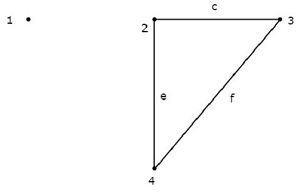
Рассмотрим график, показанный на следующем рисунке.

На этом графике узлы 2, 3 и 4 соединены двумя ветвями каждый. Но ни одна ветвь не была подключена к узлу 1 . Таким образом, узел 1 становится изолированным узлом . Следовательно, приведенный выше граф является несвязным графом .

Направленный граф

Если все ветви графа представлены стрелками, то этот граф называется ориентированным графом . Эти стрелки указывают направление протекания тока в каждой ветви. Следовательно, этот граф также называется ориентированным графом .

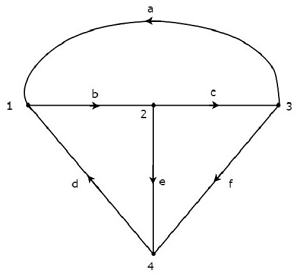
Рассмотрим график, показанный на следующем рисунке.

На приведенном выше графике направление потока тока обозначено стрелкой в ​​каждой ветви. Следовательно, это ориентированный граф .

Ненаправленный граф

Если ветви графа не представлены стрелками, то этот граф называется неориентированным графом . Поскольку нет направления потока тока, этот граф также называется неориентированным графом .

График, показанный в первом примере этой главы, является неориентированным графом , поскольку на ветвях этого графа нет стрелок.

Подграф и его виды

Часть графа называется подграфом . Мы получаем подграфы, удаляя некоторые узлы и / или ветви данного графа. Таким образом, количество ветвей и / или узлов подграфа будет меньше, чем у исходного графа. Отсюда можно сделать вывод, что подграф является подмножеством графа.

Ниже приведены два типа подграфов.

• дерево
• Co-Tree

дерево

Дерево является связным подграфом данного графа, который содержит все узлы графа. Но в этом подграфе не должно быть петель. Ветви дерева называются ветками .

Рассмотрим следующий связанный подграф графа, который показан в Примере начала этой главы.

Этот связанный подграф содержит все четыре узла данного графа и петли нет. Следовательно, это Дерево .

Это дерево имеет только три ветви из шести ветвей данного графа. Потому что, если мы рассмотрим хотя бы одну ветвь из оставшихся ветвей графа, то в вышеуказанном подграфе будет цикл. Тогда результирующий связанный подграф не будет деревом.

Из вышеприведенного дерева мы можем сделать вывод, что количество ветвей , которые присутствуют в дереве, должно быть равно n — 1, где «n» — количество узлов данного графа.

Co-Tree

Co-Tree — это подграф, который состоит из ветвей, которые удаляются при формировании дерева. Следовательно, это называется дополнением дерева. Для каждого дерева будет соответствующее Co-Tree, и его ветви называются ссылками или аккордами. В общем, ссылки представлены пунктирными линиями.

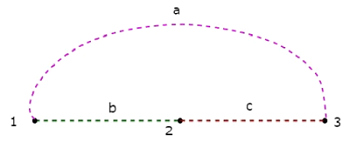
Co-Tree, соответствующее вышеуказанному дереву, показано на следующем рисунке.

Это Co-Tree имеет только три узла вместо четырех узлов данного графа, потому что Узел 4 изолирован от вышеуказанного Co-Tree. Следовательно, Co-Tree не обязательно должен быть связанным подграфом. Это Co-Tree имеет три ветви, и они образуют петлю.

Количество ветвей , присутствующих в совместном дереве, будет равно разнице между количеством ветвей данного графа и количеством веток. Математически это можно записать как

$$l = b - (n - 1)$$

$$l = b - n + 1$$

Куда,

• л количество ссылок.
• b — количество ветвей, присутствующих в данном графике.
• n — количество узлов, присутствующих в данном графе.

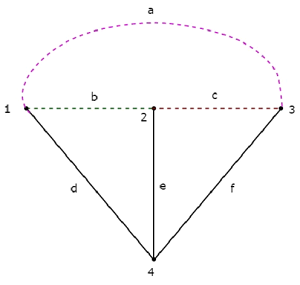
Если мы объединим дерево и соответствующее ему Co-дерево, мы получим исходный граф, как показано ниже.

Ветви дерева d, e & f представлены сплошными линиями. Ветви Co-Tree a, b & c представлены пунктирными линиями.