Теорема о передаче максимальной мощности

Количество энергии, получаемой нагрузкой, является важным параметром в электрических и электронных приложениях. В цепях постоянного тока мы можем представить нагрузку с резистором, имеющим сопротивление R _L Ом. Точно так же в цепях переменного тока мы можем представить его со сложной нагрузкой, имеющей полное сопротивление Z _L Ом.

Теорема о максимальной передаче мощности гласит, что источник постоянного напряжения будет подавать максимальную мощность на резистор переменной нагрузки только тогда, когда сопротивление нагрузки равно сопротивлению источника.

Аналогично, в теореме о максимальной передаче мощности утверждается, что источник переменного напряжения будет поставлять максимальную мощность для переменной комплексной нагрузки только тогда, когда полное сопротивление нагрузки равно комплексному сопряжению полного сопротивления источника.

В этой главе мы обсудим теорему о максимальной передаче мощности для цепей постоянного тока.

Доказательство теоремы о передаче максимальной мощности

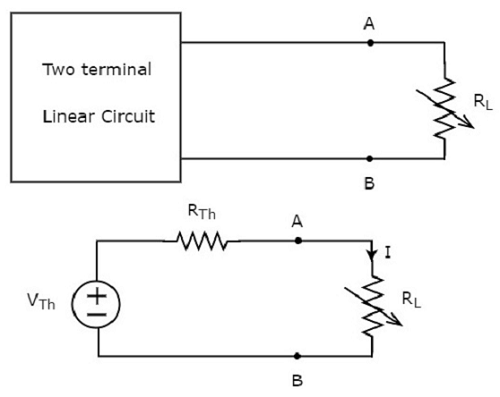
Замените любые двухполюсные линейные сети или цепи на левой стороне резистора с переменной нагрузкой, имеющего сопротивление R _L Ом, эквивалентной цепью Тевенина. Мы знаем, что эквивалентная схема Тевенина напоминает практический источник напряжения.

Эта концепция проиллюстрирована на следующих рисунках.

Количество мощности, рассеиваемой на нагрузочном резисторе, составляет

$$P_L = I ^ 2 R_L$$

Замените $I = \ frac {V_ {Th}} {R_ {Th} + R_L}$ в приведенном выше уравнении.

$$P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L$$

$\ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L) ^ 2} \ rbrace$ Уравнение 1

Условие для максимальной передачи мощности

Для максимума или минимума первая производная будет равна нулю. Итак, дифференцируем уравнение 1 относительно R _L и сделаем его равным нулю.

$$\ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L) ^ 2 \ times 1 - R_L \ times 2 (R_ {Th} + R_L) } {(R_ {Th} + R_L) ^ 4} \ rbrace = 0$$

$$\ Rightarrow (R_ {Th} + R_L) ^ 2 -2R_L (R_ {Th} + R_L) = 0$$

$$\ Rightarrow (R_ {Th} + R_L) (R_ {Th} + R_L - 2R_L) = 0$$

$$\ Rightarrow (R_ {Th} - R_L) = 0$$

 RightarrowRTh=RLилиRL=RTh $$\ Rightarrow R_ {Th} = R_L \: или \: R_L = R_ {Th}$$

Следовательно, условием максимального рассеивания мощности на нагрузке является $R_L = R_ {Th}$. Это означает, что если значение сопротивления нагрузки равно значению сопротивления источника, т. Е. Сопротивления Тевенина, то мощность, рассеиваемая на нагрузке, будет иметь максимальное значение.

Значение максимальной передачи мощности

Замените $R_L = R_ {Th} \: \ & \: P_L = P_ {L, Max}$ в уравнении 1.

$$P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th}) ^ 2} \ rbrace$$

$$P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace$$

$$\ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}}$$

 RightarrowPL,Max= fracVTh24RL,стехпоркакRL=RTh $$\ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}, \: с тех пор как \: R_ {L} = R_ {Th}$$

Следовательно, максимальная мощность, передаваемая нагрузке, составляет

$$P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}}$$

Эффективность передачи максимальной мощности

Мы можем рассчитать эффективность передачи максимальной мощности, $\ eta_ {Max}$, используя следующую формулу.

$\ eta_ {Max} = \ frac {P_ {L, Max}} {P_S}$ Уравнение 2

Куда,

• $P_ {L, Max}$ — это максимальное количество энергии, передаваемой нагрузке.

• $P_S$ — количество энергии, генерируемой источником.

$P_ {L, Max}$ — это максимальное количество энергии, передаваемой нагрузке.

$P_S$ — количество энергии, генерируемой источником.

Количество энергии, генерируемой источником

$$P_S = 2 I ^ 2 R_ {Th} + I ^ 2 R_L$$

 RightarrowPS=2I2RTh,сRL=RTh $$\ Rightarrow P_S = 2 I ^ 2 R_ {Th}, \: с \: R_ {L} = R_ {Th}$$

• Замените $I = \ frac {V_ {Th}} {2 R_ {Th}}$ в приведенном выше уравнении.

Замените $I = \ frac {V_ {Th}} {2 R_ {Th}}$ в приведенном выше уравнении.

$$P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th}$$

$$\ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th}$$

$$\ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th}}$$

• Подставьте значения $P_ {L, Max}$ и $P_S$ в уравнение 2.

Подставьте значения $P_ {L, Max}$ и $P_S$ в уравнение 2.

$$\ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} { 2R_ {Th}} \ rgroup}$$

$$\ Rightarrow \ eta_ {Max} = \ frac {1} {2}$$

Мы можем представить эффективность передачи максимальной мощности в процентах следующим образом:

$$\% \ eta_ {Max} = \ eta_ {Max} \ times 100 \%$$

$$\ Rightarrow \% \ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ times 100 \%$$

$$\ Rightarrow \% \ eta_ {Max} = 50 \%$$

Следовательно, эффективность передачи максимальной мощности составляет 50% .

пример

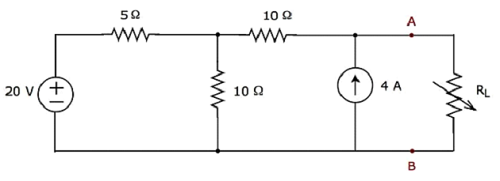
Найдите максимальную мощность, которая может быть подана на нагрузочный резистор R _L цепи, показанной на следующем рисунке.

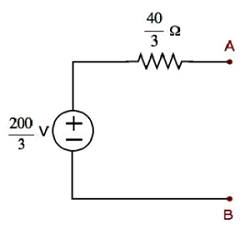
Шаг 1 — В главе «Теорема Тевенина» мы вычислили эквивалентную схему Тевенина с левой стороны клемм A и B. Теперь мы можем использовать эту схему. Это показано на следующем рисунке.

Здесь напряжение Тевенина $V_ {Th} = \ frac {200} {3} V$ и сопротивление Тевенина $R_ {Th} = \ frac {40} {3} \ Omega$

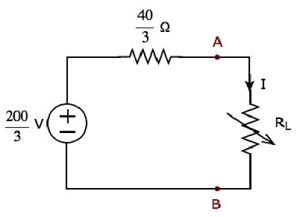
Шаг 2 — Замените часть цепи, которая находится с левой стороны от клемм A и B данной цепи, с вышеуказанной эквивалентной схемой Thevenin. Результирующая принципиальная схема показана на следующем рисунке.

Шаг 3 — Мы можем найти максимальную мощность, которая будет подана на нагрузочный резистор, R _L , используя следующую формулу.

$$P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}}$$

Замените $V_ {Th} = \ frac {200} {3} V$ и $R_ {Th} = \ frac {40} {3} \ Omega$ в приведенной выше формуле.

$$P_ {L, Max} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup}$$

$$P_ {L, Max} = \ frac {250} {3} W$$

Следовательно, максимальная мощность, которая будет подаваться на нагрузочный резистор RL данной цепи, составляет $\ mathbf {\ frac {250} {3}}$ W