Теория сети — преобразование дельты в звезды

В предыдущей главе мы обсудили пример проблемы, связанной с эквивалентным сопротивлением. Там мы легко вычислили эквивалентное сопротивление между клеммами A и B данной электрической сети. Потому что на каждом этапе мы получаем комбинацию резисторов, которые соединены в последовательной или параллельной форме.

Однако в некоторых ситуациях сложно упростить сеть, следуя предыдущему подходу. Например, резисторы подключены либо в форме треугольника (δ), либо в форме звезды. В таких ситуациях нам необходимо преобразовать сеть одной формы в другую, чтобы еще больше упростить ее, используя последовательную комбинацию или параллельную комбинацию. В этой главе давайте поговорим о преобразовании дельты в звезды .

Delta Network

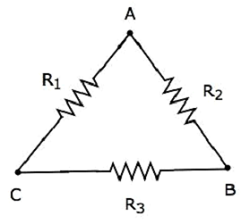
Рассмотрим следующую дельта-сеть, как показано на следующем рисунке.

Следующие уравнения представляют эквивалентное сопротивление между двумя терминалами сети треугольника, когда третий терминал остается открытым.

$$R_ {AB} = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3}$$

$$R_ {BC} = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3}$$

$$R_ {CA} = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3}$$

Звездная Сеть

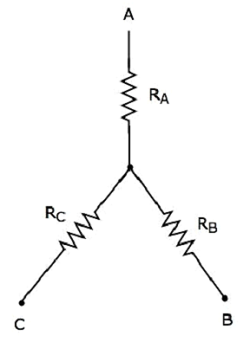
На следующем рисунке показана эквивалентная звездная сеть, соответствующая вышеуказанной дельта-сети.

Следующие уравнения представляют эквивалентное сопротивление между двумя выводами звездной сети, когда третий вывод остается открытым.

$$R_ {AB} = R_A + R_B$$

$$R_ {BC} = R_B + R_C$$

$$R_ {CA} = R_C + R_A$$

Сопротивления звездной сети с точки зрения сопротивлений сети Delta

Мы получим следующие уравнения, приравняв правые члены приведенных выше уравнений, для которых левые члены одинаковы.

$R_A + R_B = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3}$ Уравнение 1

$R_B + R_C = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3}$ Уравнение 2

$R_C + R_A = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3}$ Уравнение 3

Добавив три приведенных выше уравнения, мы получим

$$2 (R_A + R_B + R_C) = \ frac {2 (R_1 R_2 + R_2 R_3 + R_3 R_1)} {R_1 + R_2 + R_3}$$

$\ Rightarrow R_A + R_B + R_C = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3}$ Уравнение 4

Вычтите уравнение 2 из уравнения 4.

$R_A + R_B + R_C - (R_B + R_C) = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} - \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3}$

$$R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3}$$

Вычитая уравнение 3 из уравнения 4, мы получим

$$R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3}$$

Вычитая уравнение 1 из уравнения 4, мы получим

$$R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3}$$

Используя приведенные выше соотношения, мы можем найти сопротивления звездной сети из сопротивлений дельта-сети. Таким образом, мы можем преобразовать дельта-сеть в звездную сеть .

пример

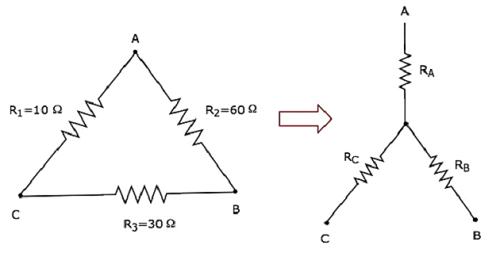
Рассчитаем сопротивления звездной сети , которые эквивалентны сопротивлению дельта-сети, как показано на следующем рисунке.

Учитывая сопротивления дельта сети как R ₁ = 10 Ом, R ₂ = 60 Ом и R ₃ = 30 Ом.

Нам известны следующие соотношения сопротивлений звездной сети в терминах сопротивлений дельта-сети.

$$R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3}$$

$$R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3}$$

$$R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3}$$

Подставим значения R ₁ , R ₂ и R ₃ в приведенные выше уравнения.

$$R_A = \ frac {10 \ times 60} {10 + 60 + 30} = \ frac {600} {100} = 6 \ Omega$$

$$R_B = \ frac {60 \ times 30} {10 + 60 + 30} = \ frac {1800} {100} = 18 \ Omega$$

$$R_C = \ frac {30 \ times 10} {10 + 60 + 30} = \ frac {300} {100} = 3 \ Omega$$

Итак, мы получили сопротивления звездной сети как R _A = 6 Ом, R _B = 18 Ом; и R _C = 3 Ом; , которые эквивалентны сопротивлениям данной дельта-сети.