Теория сети — Обзор

Теория сетей — это исследование решения проблем электрических цепей или электрических сетей. В этой вводной главе давайте сначала обсудим базовую терминологию электрических цепей и типы сетевых элементов.

Основная терминология

В теории сетей мы часто сталкиваемся со следующими терминами:

• Электрическая цепь
• Электрическая сеть
• Текущий
• вольтаж
• Мощность

Поэтому крайне важно, чтобы мы собрали некоторые базовые знания по этим условиям, прежде чем продолжить. Давайте начнем с электрической цепи.

Электрическая цепь

Электрическая цепь содержит замкнутый путь для обеспечения потока электронов от источника напряжения или источника тока. Элементы, присутствующие в электрической цепи, будут соединены последовательно, параллельно или в любой комбинации последовательно и параллельно.

Электрическая сеть

Электрическая сеть не должна содержать замкнутый путь для обеспечения потока электронов от источника напряжения или источника тока. Следовательно, мы можем сделать вывод, что «все электрические цепи являются электрическими сетями», но обратное утверждение не обязательно должно быть правдой.

Текущий

Ток «I», протекающий через проводник, является ничем иным, как скоростью потока заряда. Математически это можно записать как

$$ I = \ frac {dQ} {dt} $$

Куда,

• Q — заряд, а его единица — колумб.

• t — время, а его единица — секунда.

Q — заряд, а его единица — колумб.

t — время, а его единица — секунда.

В качестве аналогии электрический ток можно рассматривать как поток воды через трубу. Ток измеряется в амперах .

В общем случае ток электрона течет от отрицательной клеммы источника к положительной клемме, тогда как обычный ток течет от положительной клеммы источника к отрицательной клемме.

Ток электронов получается из-за движения свободных электронов, тогда как обычный ток получается из-за движения свободных положительных зарядов. Оба они называются электрическим током .

вольтаж

Напряжение «V» — это не что иное, как электродвижущая сила, которая заставляет заряд (электроны) течь. Математически это можно записать как

$$ V = \ frac {dW} {dQ} $$

Куда,

• W — потенциальная энергия, а ее единица — джоуль.

• Q — заряд, а его единица — колумб.

W — потенциальная энергия, а ее единица — джоуль.

Q — заряд, а его единица — колумб.

В качестве аналогии, напряжение можно рассматривать как давление воды, которое заставляет воду течь по трубе. Он измеряется в вольт .

Мощность

Мощность «Р» — это не что иное, как скорость потока электрической энергии. Математически это можно записать как

$$ P = \ frac {dW} {dt} $$

Куда,

• W — это электрическая энергия, и она измеряется в Джоулях .

• t — это время, и оно измеряется в секундах.

W — это электрическая энергия, и она измеряется в Джоулях .

t — это время, и оно измеряется в секундах.

Мы можем переписать приведенное выше уравнение

$$ P = \ frac {dW} {dt} = \ frac {dW} {dQ} \ times \ frac {dQ} {dt} = VI $$

Следовательно, мощность — это не что иное, как произведение напряжения V и тока I. Её единица — Ватт .

Типы сетевых элементов

Мы можем классифицировать элементы сети на различные типы на основе некоторых параметров. Ниже приведены типы элементов сети —

• Активные элементы и пассивные элементы

• Линейные элементы и нелинейные элементы

• Двусторонние элементы и односторонние элементы

Активные элементы и пассивные элементы

Линейные элементы и нелинейные элементы

Двусторонние элементы и односторонние элементы

Активные элементы и пассивные элементы

Мы можем классифицировать элементы сети как активные или пассивные в зависимости от способности обеспечивать мощность.

• Активные элементы передают энергию другим элементам, которые присутствуют в электрической цепи. Иногда они могут поглощать энергию как пассивные элементы. Это означает, что активные элементы обладают способностью передавать и поглощать энергию. Примеры : источники напряжения и источники тока.

• Пассивные элементы не могут передавать энергию (энергию) другим элементам, однако они могут поглощать энергию. Это означает, что эти элементы либо рассеивают энергию в форме тепла, либо накапливают энергию в форме магнитного или электрического поля. Примеры : резисторы, индукторы и конденсаторы.

Активные элементы передают энергию другим элементам, которые присутствуют в электрической цепи. Иногда они могут поглощать энергию как пассивные элементы. Это означает, что активные элементы обладают способностью передавать и поглощать энергию. Примеры : источники напряжения и источники тока.

Пассивные элементы не могут передавать энергию (энергию) другим элементам, однако они могут поглощать энергию. Это означает, что эти элементы либо рассеивают энергию в форме тепла, либо накапливают энергию в форме магнитного или электрического поля. Примеры : резисторы, индукторы и конденсаторы.

Линейные элементы и нелинейные элементы

Мы можем классифицировать сетевые элементы как линейные или нелинейные на основе их характеристики, чтобы подчиняться свойству линейности.

• Линейные элементы — это элементы, которые показывают линейную зависимость между напряжением и током. Примеры : резисторы, индукторы и конденсаторы.

• Нелинейные элементы — это элементы , которые не показывают линейной зависимости между напряжением и током. Примеры : источники напряжения и источники тока.

Линейные элементы — это элементы, которые показывают линейную зависимость между напряжением и током. Примеры : резисторы, индукторы и конденсаторы.

Нелинейные элементы — это элементы , которые не показывают линейной зависимости между напряжением и током. Примеры : источники напряжения и источники тока.

Двусторонние элементы и односторонние элементы

Элементы сети также могут быть классифицированы как двусторонние или односторонние в зависимости от направления потоков тока через элементы сети.

Двусторонние элементы — это элементы, которые пропускают ток в обоих направлениях и обеспечивают одинаковое сопротивление в любом направлении потока тока. Примеры : резисторы, индукторы и конденсаторы.

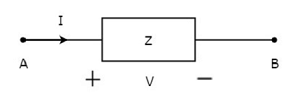
Концепция двухсторонних элементов иллюстрируется на следующих рисунках.

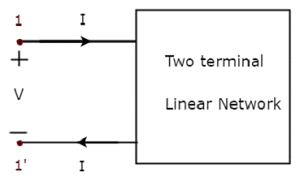
На приведенном выше рисунке ток (I) течет от клемм A к B через пассивный элемент, имеющий полное сопротивление Z Ом. Это отношение напряжения (V) на этом элементе между клеммами A и B и током (I).

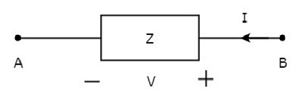
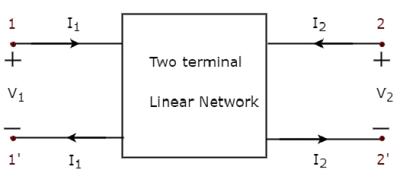
На приведенном выше рисунке ток (I) течет от клемм B к A через пассивный элемент, имеющий полное сопротивление Z Ω. Это означает, что ток (–I) течет от клемм A к B. В этом случае мы также получим одно и то же значение импеданса, поскольку и ток, и напряжение имеют отрицательные знаки относительно клемм A и B.

Односторонние элементы — это те, которые допускают ток только в одном направлении. Следовательно, они предлагают разные сопротивления в обоих направлениях.

Теория сети — пример задач

Мы обсуждали типы сетевых элементов в предыдущей главе. Теперь давайте определим природу сетевых элементов по характеристикам VI, приведенным в следующих примерах.

Пример 1

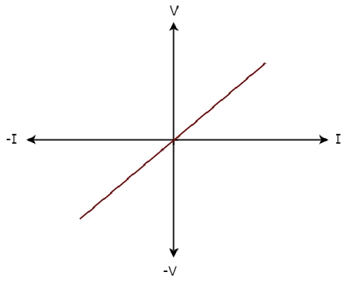
Характеристики VI сетевого элемента показаны ниже.

Шаг 1 — Проверка сетевого элемента как линейного или нелинейного .

Из приведенного выше рисунка VI характеристики сетевого элемента — это прямая линия, проходящая через начало координат. Следовательно, это линейный элемент .

Шаг 2 — Проверка сетевого элемента как активного или пассивного .

Данные характеристики VI сетевого элемента лежат в первом и третьем квадрантах.

• В первом квадранте значения напряжения (V) и тока (I) являются положительными. Таким образом, отношения напряжения (V) и тока (I) дают положительные значения импеданса.

• Аналогично, в третьем квадранте значения напряжения (V) и тока (I) имеют отрицательные значения. Таким образом, отношения напряжения (V) и тока (I) дают положительные значения импеданса.

В первом квадранте значения напряжения (V) и тока (I) являются положительными. Таким образом, отношения напряжения (V) и тока (I) дают положительные значения импеданса.

Аналогично, в третьем квадранте значения напряжения (V) и тока (I) имеют отрицательные значения. Таким образом, отношения напряжения (V) и тока (I) дают положительные значения импеданса.

Поскольку данные характеристики ВП дают положительные значения импеданса, сетевой элемент является пассивным элементом .

Шаг 3 — Проверка сетевого элемента как двустороннего или одностороннего .

Для каждой точки (I, V) на характеристиках существует соответствующая точка (-I, -V) на данных характеристиках. Следовательно, сетевой элемент является двусторонним элементом .

Следовательно, данные характеристики ВП показывают, что сетевой элемент является линейным, пассивным и двусторонним элементом .

Пример 2

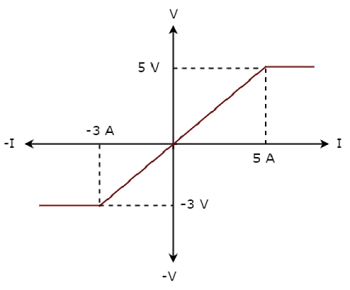
Характеристики VI сетевого элемента показаны ниже.

Шаг 1 — Проверка сетевого элемента как линейного или нелинейного .

Из приведенного выше рисунка характеристики VI сетевого элемента представляют собой прямую линию только между точками (-3A, -3V) и (5A, 5V). За этими точками характеристики VI не следуют линейной зависимости. Следовательно, это нелинейный элемент .

Шаг 2 — Проверка сетевого элемента как активного или пассивного .

Данные характеристики VI сетевого элемента лежат в первом и третьем квадрантах. В этих двух квадрантах отношения напряжения (V) и тока (I) дают положительные значения полного сопротивления. Следовательно, сетевой элемент является пассивным элементом .

Шаг 3 — Проверка сетевого элемента как двустороннего или одностороннего .

Рассмотрим точку (5А, 5В) на характеристиках. Соответствующая точка (-5A, -3V) существует по заданным характеристикам вместо (-5A, -5V). Следовательно, сетевой элемент является односторонним элементом .

Следовательно, данные характеристики ВП показывают, что сетевой элемент является нелинейным, пассивным и односторонним элементом .

Теория сети — активные элементы

Активные элементы — это сетевые элементы, которые передают энергию другим элементам, присутствующим в электрической цепи. Итак, активные элементы также называются источниками напряжения или типа тока. Мы можем классифицировать эти источники в следующие две категории —

• Независимые источники
• Зависимые источники

Независимые источники

Как следует из названия, независимые источники производят фиксированные значения напряжения или тока, и они не зависят от каких-либо других параметров. Независимые источники могут быть далее разделены на следующие две категории —

• Независимые источники напряжения
• Независимые источники тока

Независимые источники напряжения

Независимый источник напряжения создает постоянное напряжение на своих двух клеммах. Это напряжение не зависит от величины тока, который протекает через две клеммы источника напряжения.

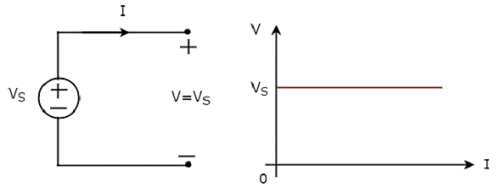
Независимый источник идеального напряжения и его характеристики ВИ показаны на следующем рисунке.

Характеристики VI независимого идеального источника напряжения представляют собой постоянную линию, которая всегда равна напряжению источника (VS) независимо от значения тока (I). Итак, внутреннее сопротивление независимого идеального источника напряжения равно нулю.

Следовательно, независимые идеальные источники напряжения практически не существуют , потому что будет некоторое внутреннее сопротивление.

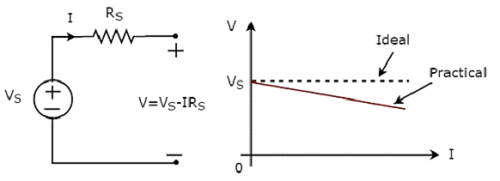
Независимый источник практического напряжения и его характеристики ВИ показаны на следующем рисунке.

Имеются отклонения характеристик ВП независимого источника практического напряжения от характеристик ВИ независимого источника идеального напряжения. Это связано с падением напряжения на внутреннем сопротивлении (R _S ) независимого практического источника напряжения.

Независимые источники тока

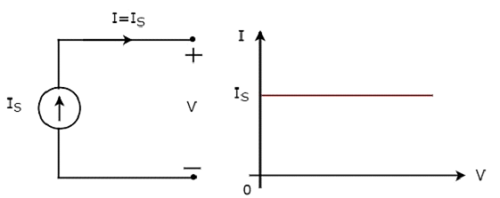
Независимый источник тока производит постоянный ток. Этот ток не зависит от напряжения на двух клеммах. Независимый идеальный источник тока и его характеристики ВИ показаны на следующем рисунке.

Характеристики ВИ независимого идеального источника тока — это постоянная линия, которая всегда равна току источника (I _S ) независимо от значения напряжения (V). Таким образом, внутреннее сопротивление независимого идеального источника тока равно бесконечным Ом.

Следовательно, независимых идеальных источников тока практически не существует , потому что будет некоторое внутреннее сопротивление.

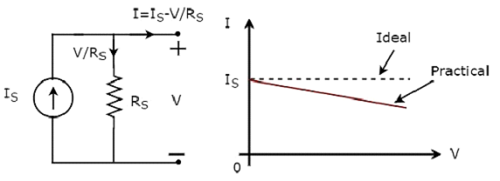
Независимый практический источник тока и его характеристики ВИ показаны на следующем рисунке.

Существует отклонение характеристик VI независимого практического источника тока от характеристик VI независимого идеального источника тока. Это происходит из-за количества тока, протекающего через внутреннее шунтирующее сопротивление (R _S ) независимого практического источника тока.

Зависимые источники

Как следует из названия, зависимые источники производят величину напряжения или тока, которая зависит от некоторого другого напряжения или тока. Зависимые источники также называются контролируемыми источниками . Зависимые источники могут быть далее разделены на следующие две категории —

• Зависимые источники напряжения
• Зависимые источники тока

Зависимые источники напряжения

Зависимый источник напряжения создает напряжение на своих двух клеммах. Величина этого напряжения зависит от некоторого другого напряжения или тока. Следовательно, зависимые источники напряжения могут быть далее классифицированы на следующие две категории —

• Зависимый от напряжения источник напряжения (VDVS)
• Зависимый от тока источник напряжения (CDVS)

Зависимые источники напряжения представлены знаками «+» и «-» внутри ромбовидной формы. Величина источника напряжения может быть представлена ​​вне формы ромба.

Зависимые источники тока

Зависимый источник тока производит ток. Величина этого тока зависит от некоторого другого напряжения или тока. Следовательно, зависимые источники тока могут быть далее классифицированы на следующие две категории —

• Зависимый от напряжения источник тока (VDCS)
• Зависимый от тока источник тока (CDCS)

Зависимые источники тока представлены стрелкой внутри ромба. Величина источника тока может быть представлена ​​вне формы ромба.

Мы можем наблюдать эти зависимые или контролируемые источники в эквивалентных моделях транзисторов.

Техника преобразования источника

Мы знаем, что существует два практических источника: источник напряжения и источник тока . Мы можем преобразовать (преобразовать) один источник в другой на основе требований, решая проблемы сети.

Техника преобразования одного источника в другой называется техникой преобразования источника . Ниже приведены два возможных преобразования источника:

• Практический источник напряжения в практический источник тока
• Практический источник тока в практический источник напряжения

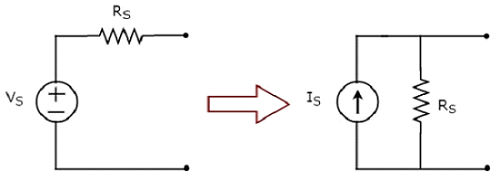
Практический источник напряжения в практический источник тока

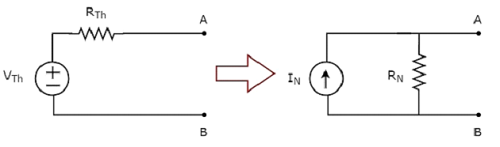
Преобразование практического источника напряжения в практический источник тока показано на следующем рисунке.

Практический источник напряжения состоит из источника напряжения (V _S ), включенного последовательно с резистором (R _S ). Это может быть преобразовано в практический источник тока, как показано на рисунке. Он состоит из источника тока (I _S ) параллельно с резистором (R _S ).

Значение IS будет равно отношению V _S и R _S. Математически это можно представить как

$$ I_S = \ frac {V_S} {R_S} $$

Практический источник тока в практический источник напряжения

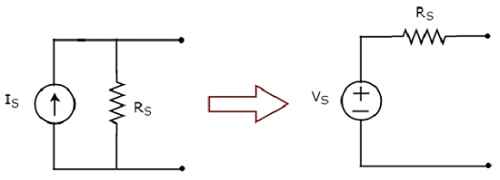
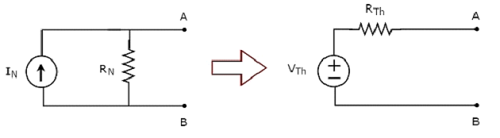
Преобразование практического источника тока в практический источник напряжения показано на следующем рисунке.

Практический источник тока состоит из источника тока (I _S ) параллельно с резистором (R _S ). Это может быть преобразовано в практический источник напряжения, как показано на рисунке. Он состоит из источника напряжения (V _S ), включенного последовательно с резистором (R _S ).

Значение V _S будет равно произведению I _S и R _S. Математически это можно представить как

$$ V_S = I_S R_S $$

Теория сети — пассивные элементы

В этой главе мы подробно обсудим пассивные элементы, такие как резистор, индуктор и конденсатор. Давайте начнем с резисторов.

резистор

Основная функциональность резистора либо противодействует, либо ограничивает протекание электрического тока. Следовательно, резисторы используются для ограничения величины тока и / или деления (разделения) напряжения.

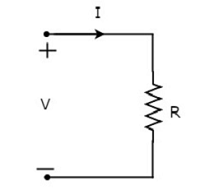
Пусть ток, протекающий через резистор, равен 1 А, а напряжение на нем составляет V вольт. Символ резистора вместе с током I и напряжением V показан на следующем рисунке.

Согласно закону Ома , напряжение на резисторе является произведением тока, протекающего через него, на сопротивление этого резистора. Математически это можно представить как

$ V = IR $ Уравнение 1

$ \ Rightarrow I = \ frac {V} {R} $ Уравнение 2

Где R сопротивление резистора.

Из уравнения 2 можно сделать вывод, что ток, протекающий через резистор, прямо пропорционален приложенному напряжению на резисторе и обратно пропорционален сопротивлению резистора.

Мощность в элементе электрической цепи может быть представлена ​​как

$ P = VI $ Уравнение 3

Заменить уравнение 1 в уравнении 3.

$ P = (IR) I $

$ \ Rightarrow P = I ^ 2 R $ Уравнение 4

Заменить уравнение 2 в уравнении 3.

$ P = V \ lgroup \ frac {V} {R} \ rgroup $

$ \ Rightarrow P = \ frac {V ^ 2} {R} $ Уравнение 5

Таким образом, мы можем рассчитать величину мощности, рассеиваемой в резисторе, используя одну из формул, упомянутых в уравнениях 3-5.

Катушка индуктивности

В общем, индукторы будут иметь количество витков. Следовательно, они производят магнитный поток, когда ток течет через него. Таким образом, величина общего магнитного потока, создаваемого индуктором, зависит от тока, протекающего через него, и они имеют линейную зависимость.

Математически это можно записать как

$$ \ Psi \: \ alpha \: I $$

$$ \ Rightarrow \ Psi = LI $$

Куда,

• Ψ — общий магнитный поток

• L — индуктивность индуктора

Ψ — общий магнитный поток

L — индуктивность индуктора

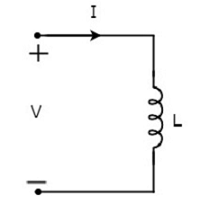
Пусть ток, протекающий через индуктор, равен 1 А, а напряжение на нем составляет V вольт. Символ индуктора вместе с током I и напряжением V показан на следующем рисунке.

Согласно закону Фарадея , напряжение на индуктивности может быть записано как

$$ V = \ frac {d \ Psi} {dt} $$

Подставим Ψ = LI в приведенном выше уравнении.

$$ V = \ frac {d (LI)} {dt} $$

$$ \ Rightarrow V = L \ frac {dI} {dt} $$

$$ \ Rightarrow I = \ frac {1} {L} \ int V dt $$

Из приведенных выше уравнений можно сделать вывод, что существует линейная зависимость между напряжением на индуктивности и током, протекающим через него.

Мы знаем, что мощность в элементе электрической цепи может быть представлена ​​как

$$ P = VI $$

Замените $ V = L \ frac {dI} {dt} $ в вышеприведенном уравнении.

$$ P = \ lgroup L \ frac {dI} {dt} \ rgroup I $$

$$ \ Rightarrow P = LI \ frac {dI} {dt} $$

Интегрируя вышеприведенное уравнение, мы получим энергию, запасенную в индукторе, в виде

$$ W = \ frac {1} {2} LI ^ 2 $$

Итак, индуктор накапливает энергию в виде магнитного поля.

Конденсатор

Как правило, конденсатор имеет две проводящие пластины, разделенные диэлектрической средой. Если положительное напряжение подается на конденсатор, то оно сохраняет положительный заряд. Точно так же, если отрицательное напряжение приложено к конденсатору, то это сохраняет отрицательный заряд.

Таким образом, количество заряда, хранящегося в конденсаторе, зависит от приложенного напряжения V на нем, и они имеют линейную зависимость. Математически это можно записать как

$$ Q \: \ alpha \: V $$

$$ \ Rightarrow Q = CV $$

Куда,

• Q — заряд, хранящийся в конденсаторе.

• С — емкость конденсатора.

Q — заряд, хранящийся в конденсаторе.

С — емкость конденсатора.

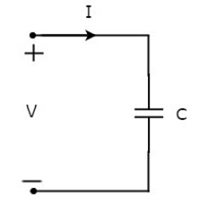
Пусть ток, протекающий через конденсатор, составляет 1 А, а напряжение на нем составляет V вольт. Символ конденсатора вместе с током I и напряжением V показан на следующем рисунке.

Мы знаем, что ток — это не что иное, как скорость потока заряда . Математически это можно представить как

$$ I = \ frac {dQ} {dt} $$

Замените $ Q = CV $ в приведенном выше уравнении.

$$ I = \ frac {d (CV)} {dt} $$

$$ \ Rightarrow I = C \ frac {dV} {dt} $$

$$ \ Rightarrow V = \ frac {1} {C} \ int I dt $$

Из приведенных выше уравнений можно сделать вывод, что существует линейная зависимость между напряжением на конденсаторе и током, протекающим через него.

Мы знаем, что мощность в элементе электрической цепи может быть представлена ​​как

$$ P = VI $$

Замените $ I = C \ frac {dV} {dt} $ в вышеприведенном уравнении.

$$ P = V \ lgroup C \ frac {dV} {dt} \ rgroup $$

$$ \ Rightarrow P = CV \ frac {dV} {dt} $$

Интегрируя вышеприведенное уравнение, мы получим энергию, накопленную в конденсаторе как

$$ W = \ frac {1} {2} CV ^ 2 $$

Итак, конденсатор накапливает энергию в виде электрического поля.

Теория сетей — законы Кирхгофа

Сетевые элементы могут быть как активного, так и пассивного типа. Любая электрическая цепь или сеть содержит один из этих двух типов сетевых элементов или их комбинацию.

Теперь давайте поговорим о следующих двух законах, которые широко известны как законы Кирхгофа .

• Текущий закон Кирхгофа
• Закон напряжения Кирхгофа

Текущий закон Кирхгофа

Текущий закон Кирхгофа (KCL) гласит, что алгебраическая сумма токов, покидающих (или входящих) в узел, равна нулю.

Узел — это точка, в которой к нему подключены два или более элементов схемы. Если только два элемента схемы связаны с узлом, то это называется простым узлом. Если три или более элементов схемы подключены к узлу, то он называется основным узлом .

Математически KCL можно представить как

$$ \ displaystyle \ sum \ limit_ {m = 1} ^ M I_m = 0 $$

Куда,

• I _m — это ток m- ^й ветви, покидающей узел.

• M — количество ветвей, которые связаны с узлом.

I _m — это ток m- ^й ветви, покидающей узел.

M — количество ветвей, которые связаны с узлом.

Вышеупомянутое утверждение KCL также может быть выражено как «алгебраическая сумма токов, входящих в узел, равна алгебраической сумме токов, выходящих из узла». Давайте проверим это утверждение на следующем примере.

пример

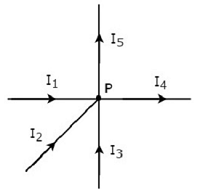
Запишите уравнение KCL в узле P следующего рисунка.

• На приведенном выше рисунке токи ветвления I ₁ , I ₂ и I ₃ входят в узел P. Итак, рассмотрим отрицательные знаки для этих трех токов.

• На приведенном выше рисунке токи ветвления I ₄ и I ₅ выходят из узла P. Итак, рассмотрим положительные признаки для этих двух токов.

На приведенном выше рисунке токи ветвления I ₁ , I ₂ и I ₃ входят в узел P. Итак, рассмотрим отрицательные знаки для этих трех токов.

На приведенном выше рисунке токи ветвления I ₄ и I ₅ выходят из узла P. Итак, рассмотрим положительные признаки для этих двух токов.

Уравнение KCL в узле P будет

$$ — I_1 — I_2 — I_3 + I_4 + I_5 = 0 $$

$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$

В приведенном выше уравнении левая часть представляет сумму входных токов, тогда как правая часть представляет сумму выходных токов.

В этом уроке мы рассмотрим положительный знак, когда ток покидает узел, и отрицательный знак, когда он входит в узел. Точно так же вы можете рассмотреть отрицательный знак, когда ток покидает узел, и положительный знак, когда он входит в узел. В обоих случаях результат будет одинаковым .

Примечание. KCL не зависит от природы сетевых элементов, которые подключены к узлу.

Закон напряжения Кирхгофа

Закон напряжения Кирхгофа (KVL) гласит, что алгебраическая сумма напряжений вокруг петли или сетки равна нулю.

Цикл — это путь, который заканчивается в том же узле, откуда он начался. Напротив, Mesh — это цикл, который не содержит внутри себя никаких других циклов.

Математически КВЛ можно представить как

$$ \ displaystyle \ sum \ limit_ {n = 1} ^ N V_n = 0 $$

Куда,

• V _n — это напряжение n- ^го элемента в петле (ячейка).

• N — количество сетевых элементов в цикле (сетке).

V _n — это напряжение n- ^го элемента в петле (ячейка).

N — количество сетевых элементов в цикле (сетке).

Вышеупомянутое утверждение KVL также может быть выражено как «алгебраическая сумма источников напряжения равна алгебраической сумме падений напряжения, которые присутствуют в контуре». Давайте проверим это утверждение с помощью следующего примера.

пример

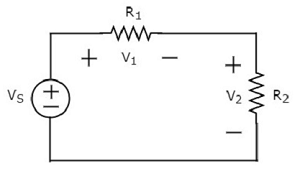
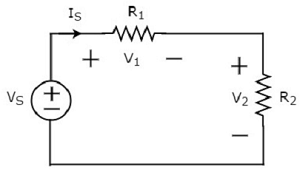
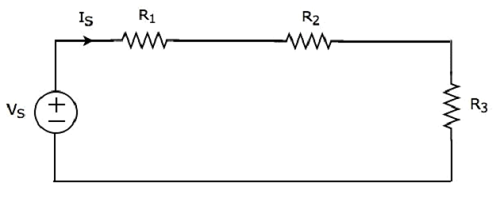
Напишите уравнение КВЛ вокруг контура следующей схемы.

Приведенная выше принципиальная схема состоит из источника напряжения, V _S, последовательно с двумя резисторами R ₁ и R ₂ . Падения напряжения на резисторах R ₁ и R ₂ составляют V ₁ и V ₂ соответственно.

Примените КВЛ вокруг петли.

$$ V_S — V_1 — V_2 = 0 $$

$$ \ Rightarrow V_S = V_1 + V_2 $$

В приведенном выше уравнении член с левой стороны представляет один источник напряжения VS. Принимая во внимание, что правая часть представляет сумму падений напряжения . В этом примере мы рассмотрели только один источник напряжения. Вот почему левая часть содержит только один термин. Если мы рассмотрим несколько источников напряжения, то левая часть содержит сумму источников напряжения.

В этом уроке мы рассматриваем знак напряжения каждого элемента как полярность второй клеммы, которая присутствует во время перемещения по контуру. Точно так же вы можете рассматривать знак каждого напряжения как полярность первого контакта, который присутствует во время перемещения по контуру. В обоих случаях результат будет одинаковым .

Примечание. KVL не зависит от природы сетевых элементов, присутствующих в цикле.

Принципы деления количества электричества

В этой главе давайте поговорим о следующих двух принципах разделения электрических величин.

• Текущий принцип деления
• Принцип деления напряжения

Текущий принцип деления

Когда два или более пассивных элемента соединены параллельно, количество тока, протекающего через каждый элемент, разделяется (разделяется) между собой от тока, который входит в узел.

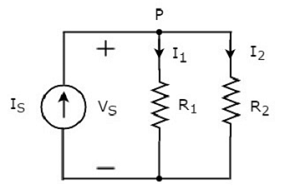
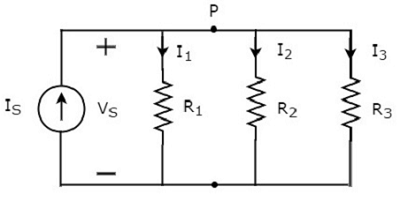
Рассмотрим следующую принципиальную схему .

Приведенная выше принципиальная схема состоит из источника входного тока I _S, параллельного двум резисторам R ₁ и R ₂ . Напряжение на каждом элементе составляет V _S. Токи, протекающие через резисторы R ₁ и R _2, представляют собой I ₁ и I ₂ соответственно.

Уравнение KCL в узле P будет

$$ I_S = I_1 + I_2 $$

• Замените $ I_1 = \ frac {V_S} {R_1} $ и $ I_2 = \ frac {V_S} {R_2} $ в вышеприведенном уравнении.

Замените $ I_1 = \ frac {V_S} {R_1} $ и $ I_2 = \ frac {V_S} {R_2} $ в вышеприведенном уравнении.

$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} \ rgroup $$

$$ \ Rightarrow V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$

• Подставьте значение V _S в $ I_1 = \ frac {V_S} {R_1} $.

Подставьте значение V _S в $ I_1 = \ frac {V_S} {R_1} $.

$$ I_1 = \ frac {I_S} {R_1} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$

$$ \ Rightarrow I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$

• Подставьте значение V _S в $ I_2 = \ frac {V_S} {R_2} $.

Подставьте значение V _S в $ I_2 = \ frac {V_S} {R_2} $.

$$ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$

$$ \ Rightarrow I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$

Из уравнений I ₁ и I ₂ можно обобщить, что ток, протекающий через любой пассивный элемент, можно найти с помощью следующей формулы.

$$ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert … \ rVert Z_ {N-1}} {Z_1 + Z_2 + … + Z_N} \ rgroup $$

Это известно как принцип деления тока и применимо, когда два или более пассивных элемента соединены параллельно и только один ток поступает в узел.

Куда,

• I _N — ток, протекающий через пассивный элемент N- ^й ветви.

• I _S — входной ток, который поступает в узел.

• Z ₁ , Z ₂ ,…, Z _N — импедансы 1- ^й ветви, 2- ^й ветви,…, N- ^й ветви соответственно.

I _N — ток, протекающий через пассивный элемент N- ^й ветви.

I _S — входной ток, который поступает в узел.

Z ₁ , Z ₂ ,…, Z _N — импедансы 1- ^й ветви, 2- ^й ветви,…, N- ^й ветви соответственно.

Принцип деления напряжения

Когда два или более пассивных элемента соединены последовательно, величина напряжения, присутствующего на каждом элементе, делится (разделяется) между собой от напряжения, которое доступно для всей этой комбинации.

Рассмотрим следующую принципиальную схему .

Приведенная выше принципиальная схема состоит из источника напряжения, V _S, последовательно с двумя резисторами R ₁ и R ₂ . Ток, протекающий через эти элементы, является I _S. Падения напряжения на резисторах R ₁ и R ₂ составляют V ₁ и V ₂ соответственно.

Уравнение КВЛ вокруг цикла будет

$$ V_S = V_1 + V_2 $$

• Замените V ₁ = I _S R ₁ и V ₂ = I _S R ₂ в приведенном выше уравнении

Замените V ₁ = I _S R ₁ и V ₂ = I _S R ₂ в приведенном выше уравнении

$$ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $$

$$ I_S = \ frac {V_S} {R_1 + R_2} $$

• Подставим значение I _S в V ₁ = I _S R ₁ .

Подставим значение I _S в V ₁ = I _S R ₁ .

$$ V_1 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_1 $$

$$ \ Rightarrow V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$

• Подставим значение I _S в V ₂ = I _S R ₂ .

Подставим значение I _S в V ₂ = I _S R ₂ .

$$ V_2 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_2 $$

$$ \ Rightarrow V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$

Из уравнений V ₁ и V ₂ можно обобщить, что напряжение на любом пассивном элементе можно найти с помощью следующей формулы.

$$ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + …. + Z_N} \ rgroup $$

Это известно как принцип деления напряжения, и оно применимо, когда два или более пассивных элемента соединены последовательно и только одно напряжение доступно во всей комбинации.

Куда,

• V _N — напряжение на N- ^м пассивном элементе.

• V _S — это входное напряжение, которое присутствует во всей комбинации последовательных пассивных элементов.

• Z ₁ , Z ₂ ,…, Z ₃ — импедансы 1- ^го пассивного элемента, 2- ^го пассивного элемента,…, N- ^го пассивного элемента соответственно.

V _N — напряжение на N- ^м пассивном элементе.

V _S — это входное напряжение, которое присутствует во всей комбинации последовательных пассивных элементов.

Z ₁ , Z ₂ ,…, Z ₃ — импедансы 1- ^го пассивного элемента, 2- ^го пассивного элемента,…, N- ^го пассивного элемента соответственно.

Теория сети — узловой анализ

Есть два основных метода, которые используются для решения любой электрической сети: узловой анализ и анализ сетки . В этой главе давайте обсудим метод анализа узлов .

В узловом анализе мы рассмотрим напряжения на узлах относительно Земли. Следовательно, анализ узлов также называется методом напряжения на узле .

Процедура узлового анализа

Выполните следующие шаги при решении любой электрической сети или цепи с использованием узлового анализа.

• Шаг 1 — Определите главные узлы и выберите один из них в качестве эталонного узла . Мы будем рассматривать этот опорный узел как Основание.

• Шаг 2 — Отметьте напряжения узлов относительно Земли со всех основных узлов, кроме эталонного узла.

• Шаг 3 — Запись узловых уравнений на все основные узлах , за исключением опорного узла. Узловое уравнение получается путем применения сначала KCL, а затем закона Ома.

• Шаг 4 — Решите узловые уравнения, полученные на шаге 3, чтобы получить напряжения узлов.

Шаг 1 — Определите главные узлы и выберите один из них в качестве эталонного узла . Мы будем рассматривать этот опорный узел как Основание.

Шаг 2 — Отметьте напряжения узлов относительно Земли со всех основных узлов, кроме эталонного узла.

Шаг 3 — Запись узловых уравнений на все основные узлах , за исключением опорного узла. Узловое уравнение получается путем применения сначала KCL, а затем закона Ома.

Шаг 4 — Решите узловые уравнения, полученные на шаге 3, чтобы получить напряжения узлов.

Теперь мы можем найти ток, протекающий через любой элемент, и напряжение на любом элементе, который присутствует в данной сети, с помощью узловых напряжений.

пример

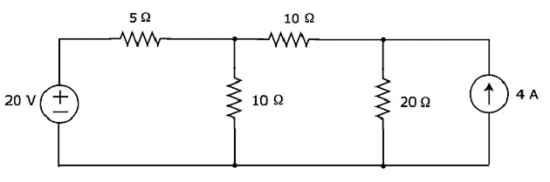
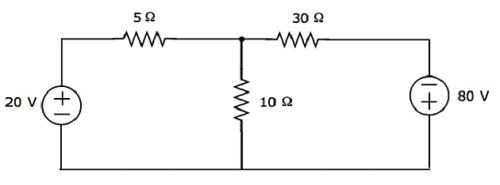
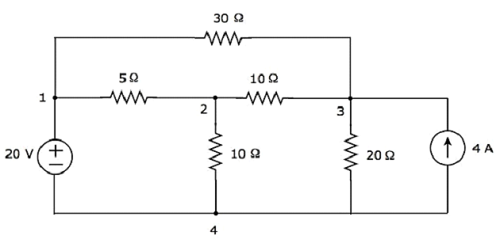
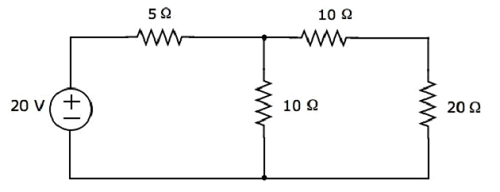
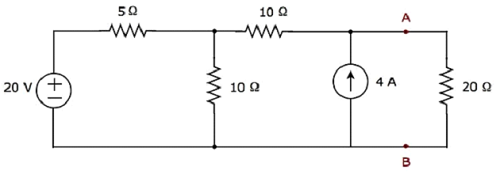
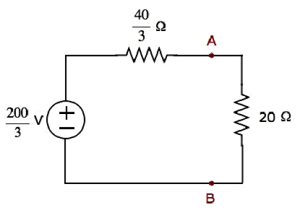
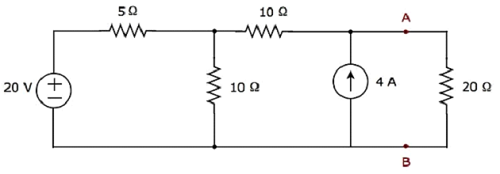
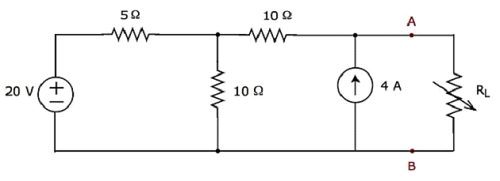
Найти ток, протекающий через резистор 20 Ом следующей цепи, используя узловой анализ .

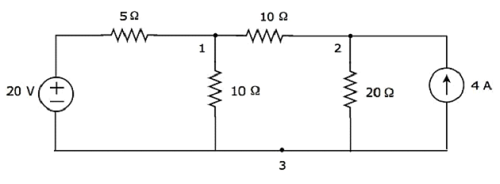
Шаг 1 — В приведенной выше схеме есть три основных узла . Они обозначены как 1, 2 и 3 на следующем рисунке.

На рисунке выше, рассмотрите узел 3 как опорный узел (Земля).

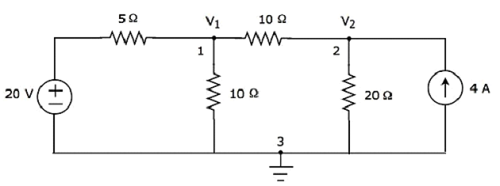
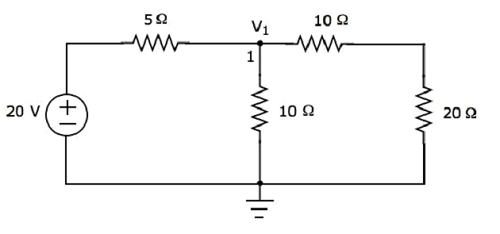
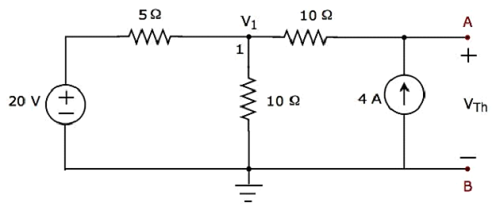
Шаг 2 — Напряжения узлов, V ₁ и V ₂ , обозначены на следующем рисунке.

На приведенном выше рисунке V ₁ — это напряжение от узла 1 относительно земли, а V ₂ — это напряжение от узла 2 относительно земли.

Шаг 3 — В этом случае мы получим два узловых уравнения , так как есть два главных узла, 1 и 2, отличных от Ground. Когда мы записываем узловые уравнения в узле, предположим, что все токи выходят из узла, для которого направление тока не упомянуто, и напряжение этого узла больше, чем напряжение других узлов в цепи.

Узловое уравнение в узле 1

$$ \ frac {V_1 — 20} {5} + \ frac {V_1} {10} + \ frac {V_1 — V_2} {10} = 0 $$

$$ \ Rightarrow \ frac {2 V_1 — 40 + V_1 + V_1 — V_2} {10} = 0 $$

$$ \ Rightarrow 4V_1 — 40 — V_2 = 0 $$

$ \ Rightarrow V_2 = 4V_1 — 40 $ Уравнение 1

Узловое уравнение в узле 2

$$ — 4 + \ frac {V_2} {20} + \ frac {V_2 — V_1} {10} = 0 $$

$$ \ Rightarrow \ frac {-80 + V_2 + 2V_2 — 2V_2} {20} = 0 $$

$ \ Rightarrow 3V_2 — 2V_1 = 80 $ Уравнение 2

Шаг 4 — Нахождение узловых напряжений V ₁ и V ₂ путем решения уравнения 1 и уравнения 2.

Заменить уравнение 1 на уравнение 2.

$$ 3 (4 V_1 — 40) — 2 V_1 = 80 $$

$$ \ Rightarrow 12 V_1 — 120 — 2V_1 = 80 $$

$$ \ Rightarrow 10 V_1 = 200 $$

$$ \ Rightarrow V_1 = 20V $$

Заменить V ₁ = 20 В в Уравнении1.

$$ V_2 = 4 (20) — 40 $$

$$ \ Rightarrow V_2 = 40V $$

Итак, мы получили напряжения узлов V ₁ и V ₂ как 20 В и 40 В соответственно.

Шаг 5 — Напряжение на резисторе 20 Ом является ничем иным, как напряжением узла V _2, и оно равно 40 В. Теперь мы можем найти ток, протекающий через резистор 20 Ом, используя закон Ома.

$$ I_ {20 \ Omega} = \ frac {V_2} {R} $$

Подставим значения V ₂ и R в вышеприведенное уравнение.

$$ I_ {20 \ Omega} = \ frac {40} {20} $$

$$ \ Rightarrow I_ {20 \ Omega} = 2A $$

Следовательно, ток, протекающий через резистор 20 Ом данной цепи, составляет 2 А.

Примечание — Из приведенного выше примера, мы можем сделать вывод , что мы должны решить «п» узловые уравнения, если электрическая цепь имеет «п» главные узлы ( за исключением опорного узла). Таким образом, мы можем выбрать узловой анализ , когда количество основных узлов ( за исключением опорного узла) меньше , чем число ячеек любой электрической цепи.

Теория сети — Сетчатый анализ

При анализе сетки мы будем рассматривать токи, протекающие через каждую сетку. Следовательно, Mesh-анализ также называется методом Mesh-current .

Ветвь — это путь, соединяющий два узла и содержащий элемент схемы. Если ветвь принадлежит только одной сетке, то ток ветви будет равен току сетки.

Если ветвь является общей для двух сеток, то ток ветвления будет равен сумме (или разности) двух сеточных токов, когда они находятся в одном (или противоположном) направлении.

Процедура анализа сетки

Выполните следующие шаги при решении любой электрической сети или цепи с использованием анализа сетки.

• Шаг 1 — Определите ячейки и отметьте токи ячейки в направлении по часовой стрелке или против часовой стрелки.

• Шаг 2 — Соблюдайте количество тока, протекающего через каждый элемент, с точки зрения сеточных токов.

• Шаг 3 — Запишите уравнения сетки для всех сеток. Сетчатое уравнение получается путем применения сначала КВЛ, а затем закона Ома.

• Шаг 4 — Решите уравнения сетки, полученные на шаге 3, чтобы получить токи сетки .

Шаг 1 — Определите ячейки и отметьте токи ячейки в направлении по часовой стрелке или против часовой стрелки.

Шаг 2 — Соблюдайте количество тока, протекающего через каждый элемент, с точки зрения сеточных токов.

Шаг 3 — Запишите уравнения сетки для всех сеток. Сетчатое уравнение получается путем применения сначала КВЛ, а затем закона Ома.

Шаг 4 — Решите уравнения сетки, полученные на шаге 3, чтобы получить токи сетки .

Теперь мы можем найти ток, протекающий через любой элемент, и напряжение на любом элементе, который присутствует в данной сети, используя токи сетки.

пример

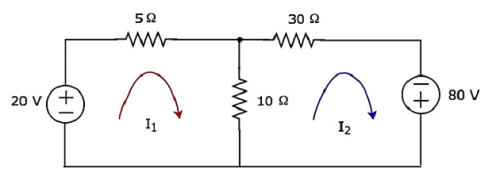
Найти напряжение на резисторе 30 Ом с помощью анализа сетки .

Шаг 1 — Есть две сетки в схеме выше. Токи сетки I ₁ и I ₂ рассматриваются по часовой стрелке. Эти сетчатые токи показаны на следующем рисунке.

Шаг 2 — Сетевой ток I ₁ протекает через источник напряжения 20 В и резистор 5 Ом. Аналогично, ток сетки I ₂ протекает через резистор 30 Ом и источник напряжения -80 В. Но разность двух сеточных токов, I ₁ и I ₂ , протекает через резистор 10 Ом, поскольку это общая ветвь двух ячеек.

Шаг 3 — В этом случае мы получим два уравнения сетки, поскольку в данной схеме есть две сетки. Когда мы запишем уравнения сетки, предположим, что ток сетки этой конкретной сетки больше, чем все другие токи сетки в схеме.

Уравнение сетки первой сетки

$$ 20 — 5I_1 -10 (I_1 — I_2) = 0 $$

$$ \ Rightarrow 20 — 15I_1 + 10I_2 = 0 $$

$$ \ Rightarrow 10I_2 = 15I_1 — 20 $$

Разделите вышеприведенное уравнение на 5.

$$ 2I_2 = 3I_1 — 4 $$

Умножьте приведенное выше уравнение на 2.

$ 4I_2 = 6I_1 — 8 $ Уравнение 1

Уравнение сетки второй сетки имеет вид

$$ — 10 (I_2 — I_1) — 30I_2 + 80 = 0 $$

Разделите вышеприведенное уравнение на 10.

$$ — (I_2 — I_1) — 3I_2 + 8 = 0 $$

$$ \ Rightarrow -4I_2 + I_1 + 8 = 0 $$

$ 4I_2 = I_1 + 8 $ Уравнение 2

Шаг 4 — Нахождение ячеистых токов I ₁ и I ₂ путем решения уравнения 1 и уравнения 2.

Термины левой части уравнения 1 и уравнения 2 одинаковы. Следовательно, приравните правые члены уравнения 1 и уравнения 2, чтобы найти значение I ₁ .

$$ 6I_1 — 8 = I_1 + 8 $$

$$ \ Rightarrow 5I_1 = 16 $$

$$ \ Rightarrow I_1 = \ frac {16} {5} A $$

Подставьте значение I ₁ в уравнение 2.

$$ 4I_2 = \ frac {16} {5} + 8 $$

$$ \ Rightarrow 4I_2 = \ frac {56} {5} $$

$$ \ Rightarrow I_2 = \ frac {14} {5} A $$

Итак, мы получили сеточные токи I ₁ и I ₂ как $ \ mathbf {\ frac {16} {5}} $ A и $ \ mathbf {\ frac {14} {5}} $ A соответственно.

Шаг 5 — Ток, протекающий через резистор 30 Ом, является ничем иным, как током сетки I _2, и он равен $ \ frac {14} {5} $ A. Теперь мы можем найти напряжение на резисторе 30 Ом, используя закон Ома ,

$$ V_ {30 \ Omega} = I_2 R $$

Подставим значения I ₂ и R в приведенное выше уравнение.

$$ V_ {30 \ Omega} = \ lgroup \ frac {14} {5} \ rgroup 30 $$

$$ \ Rightarrow V_ {30 \ Omega} = 84V $$

Следовательно, напряжение на резисторе 30 Ом данной цепи составляет 84 В.

Примечание 1. — Из приведенного выше примера мы можем сделать вывод, что нам нужно решить «m» сеточных уравнений, если электрическая цепь имеет «m» сеток. Вот почему мы можем выбрать анализ ячеек, когда число ячеек меньше числа главных узлов (кроме эталонного узла) любой электрической цепи.

Примечание 2 — Мы можем выбрать анализ узлов или анализ ячеек, когда число ячеек равно числу главных узлов (кроме эталонного узла) в любой электрической цепи.

Теория сети — эквивалентные схемы

Если цепь состоит из двух или более одинаковых пассивных элементов и соединена исключительно последовательным или параллельным типом, то мы можем заменить их одним эквивалентным пассивным элементом. Следовательно, эта схема называется эквивалентной схемой .

В этой главе давайте поговорим о следующих двух эквивалентных схемах.

• Серия Эквивалентная Схема
• Параллельная эквивалентная схема

Серия Эквивалентная Схема

Если подобные пассивные элементы соединены последовательно , то один и тот же ток будет проходить через все эти элементы. Но напряжение делится на каждый элемент.

Рассмотрим следующую принципиальную схему .

Он имеет один источник напряжения (V _S ) и три резистора, имеющих сопротивления R ₁ , R ₂ и R ₃ . Все эти элементы связаны последовательно. Ток IS течет через все эти элементы.

Вышеуказанная схема имеет только одну сетку. Уравнение КВЛ вокруг этой сетки

$$ V_S = V_1 + V_2 + V_3 $$

Замените $ V_1 = I_S R_1, \: V_2 = I_S R_2 $ и $ V_3 = I_S R_3 $ в вышеприведенном уравнении.

$$ V_S = I_S R_1 + I_S R_2 + I_S R_3 $$

$$ \ Rightarrow V_S = I_S (R_1 + R_2 + R_3) $$

Вышеупомянутое уравнение имеет вид $ V_S = I_S R_ {Eq} $ где,

$$ R_ {Eq} = R_1 + R_2 + R_3 $$

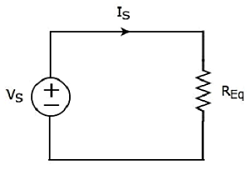
Эквивалентная принципиальная схема данной цепи показана на следующем рисунке.

Это означает, что если несколько резисторов соединены последовательно, то мы можем заменить их эквивалентным резистором . Сопротивление этого эквивалентного резистора равно сумме сопротивлений всех этих нескольких резисторов.

Примечание 1. — Если «N» индукторы, имеющие индуктивности L ₁ , L ₂ , …, L _N , соединены последовательно, то эквивалентная индуктивность будет

$$ L_ {Eq} = L_1 + L_2 + … + L_N $$

Примечание 2 — Если конденсаторы N, имеющие емкости C ₁ , C ₂ , …, C _N , соединены последовательно, то эквивалентная емкость будет

$$ \ frac {1} {C_ {Eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + … + \ frac {1} {C_N} $$

Параллельная эквивалентная схема

Если подобные пассивные элементы соединены параллельно , то одинаковое напряжение будет поддерживаться на каждом элементе. Но ток, протекающий через каждый элемент, разделяется.

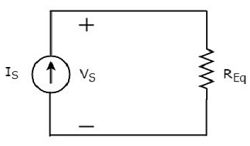
Рассмотрим следующую принципиальную схему .

Он имеет один источник тока (I _S ) и три резистора с сопротивлениями R ₁ , R ₂ и R ₃ . Все эти элементы соединены параллельно. Напряжение (V _S ) доступно для всех этих элементов.

Вышеуказанная схема имеет только один главный узел (P), кроме узла заземления. Уравнение KCL в этом главном узле (P)

$$ I_S = I_1 + I_2 + I_3 $$

Замените $ I_1 = \ frac {V_S} {R_1}, \: I_2 = \ frac {V_S} {R_2} $ и $ I_3 = \ frac {V_S} {R_3} $ в вышеприведенном уравнении.

$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} + \ frac {V_S} {R_3} $$

$$ \ Rightarrow I_S = V_S \ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup $$

$$ \ Rightarrow V_S = I_S \ left [\ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} \ right] $$

Вышеупомянутое уравнение имеет вид V _S = I _S R _Eq, где,

$$ R_ {Eq} = \ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} $$

$$ \ frac {1} {R_ {Eq}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $$

Эквивалентная принципиальная схема данной цепи показана на следующем рисунке.

Это означает, что если несколько резисторов соединены параллельно, то мы можем заменить их эквивалентным резистором. Сопротивление этого эквивалентного резистора равно обратной сумме обратной величины каждого сопротивления всех этих нескольких резисторов.

Примечание 1. — Если «N» индукторы, имеющие индуктивности L ₁ , L ₂ , …, L _N , соединены параллельно, то эквивалентная индуктивность будет

$$ \ frac {1} {L_ {Eq}} = \ frac {1} {L_1} + \ frac {1} {L_2} + … + \ frac {1} {L_N} $$

Примечание 2 — Если конденсаторы N, имеющие емкости C ₁ , C ₂ , …, C _N , подключены параллельно, то эквивалентная емкость будет

$$ C_ {Eq} = C_1 + C_2 + … + C_N $$

Эквивалентная схема Пример задачи

В предыдущей главе мы обсуждали эквивалентные схемы последовательного и параллельного объединения по отдельности. В этой главе давайте решим примерную проблему, рассматривая как последовательные, так и параллельные комбинации одинаковых пассивных элементов.

пример

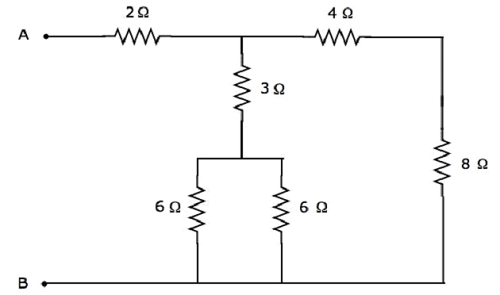
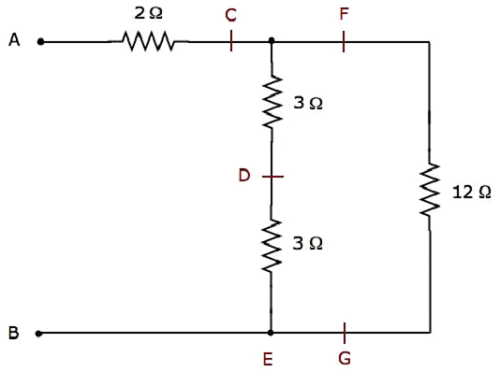
Найдем эквивалентное сопротивление на клеммах A и B следующей электрической сети.

Мы получим эквивалентное сопротивление между клеммами A и B путем минимизации вышеупомянутой сети в один резистор между этими двумя клеммами. Для этого мы должны определить комбинацию резисторов , которые соединены последовательно и параллельно, а затем найти эквивалентное сопротивление соответствующей формы на каждом шаге.

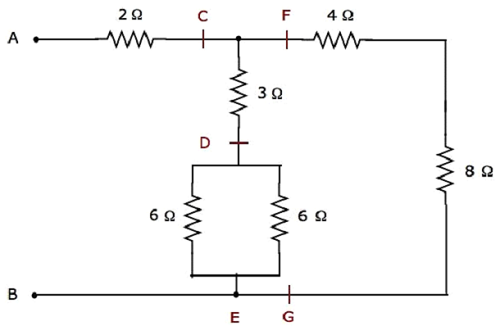
Данная электрическая сеть преобразуется в следующую форму, как показано на следующем рисунке.

На приведенном выше рисунке буквы C – G используются для обозначения различных клемм.

Шаг 1 — В описанной выше сети два резистора 6 Ом подключены параллельно . Таким образом, эквивалентное сопротивление между D & E будет 3 Ом. Это можно получить, выполнив следующее упрощение.

$$ R_ {DE} = \ frac {6 \ times 6} {6 + 6} = \ frac {36} {12} = 3 \ Omega $$

В вышеуказанной сети резисторы 4 Ом; и 8 Ом; связаны последовательно . Таким образом, эквивалентное сопротивление между F & G будет 12 Ом. Это можно получить, выполнив следующее упрощение.

$$ R_ {FG} = 4 + 8 = 12 \ Омега $$

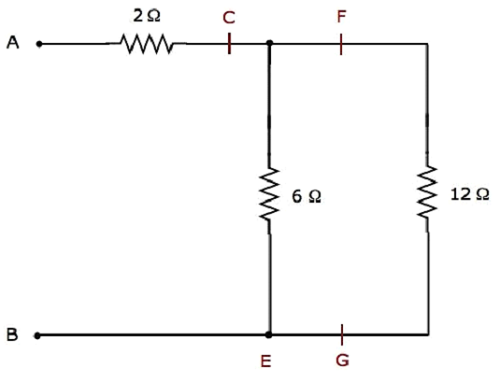
Шаг 2 — Упрощенная электрическая сеть после шага 1 показана на следующем рисунке.

В вышеуказанной сети два резистора 3 Ом соединены последовательно . Таким образом, эквивалентное сопротивление между C & E будет 6 Ом; , Это можно получить, выполнив следующее упрощение.

$$ R_ {CE} = 3 + 3 = 6 \ Омега $$

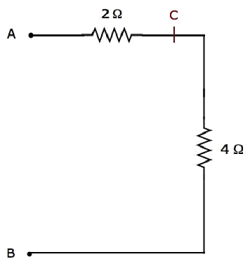
Шаг 3 — Упрощенная электрическая сеть после шага 2 показана на следующем рисунке.

В приведенной выше сети резисторы 6 Ом; и 12 Ом; соединены параллельно . Таким образом, эквивалентное сопротивление между C и B будет 4 Ом. Это можно получить, выполнив следующее упрощение.

$$ R_ {CB} = \ frac {6 \ times 12} {6 + 12} = \ frac {72} {18} = 4 \ Omega $$

Шаг 4 — Упрощенная электрическая сеть после шага 3 показана на следующем рисунке.

В приведенной выше сети резисторы 2 Ом; и 4 Ом; соединены последовательно между клеммами A и B. Таким образом, эквивалентное сопротивление между A и B будет 6 Ом. Это можно получить, выполнив следующее упрощение.

$$ R_ {AB} = 2 + 4 = 6 \ Omega $$

Следовательно, эквивалентное сопротивление между клеммами A и B данной электрической сети составляет 6 Ом; ,

Теория сети — преобразование дельты в звезды

В предыдущей главе мы обсудили пример проблемы, связанной с эквивалентным сопротивлением. Там мы легко вычислили эквивалентное сопротивление между клеммами A и B данной электрической сети. Потому что на каждом этапе мы получаем комбинацию резисторов, которые соединены в последовательной или параллельной форме.

Однако в некоторых ситуациях сложно упростить сеть, следуя предыдущему подходу. Например, резисторы подключены либо в форме треугольника (δ), либо в форме звезды. В таких ситуациях нам необходимо преобразовать сеть одной формы в другую, чтобы еще больше упростить ее, используя последовательную комбинацию или параллельную комбинацию. В этой главе давайте поговорим о преобразовании дельты в звезды .

Delta Network

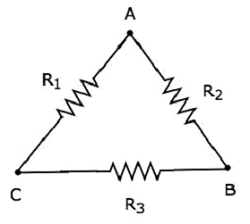
Рассмотрим следующую дельта-сеть, как показано на следующем рисунке.

Следующие уравнения представляют эквивалентное сопротивление между двумя терминалами сети треугольника, когда третий терминал остается открытым.

$$ R_ {AB} = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $$

$$ R_ {BC} = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $$

$$ R_ {CA} = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $$

Звездная Сеть

На следующем рисунке показана эквивалентная звездная сеть, соответствующая вышеуказанной дельта-сети.

Следующие уравнения представляют эквивалентное сопротивление между двумя выводами звездной сети, когда третий вывод остается открытым.

$$ R_ {AB} = R_A + R_B $$

$$ R_ {BC} = R_B + R_C $$

$$ R_ {CA} = R_C + R_A $$

Сопротивления звездной сети с точки зрения сопротивлений сети Delta

Мы получим следующие уравнения, приравняв правые члены приведенных выше уравнений, для которых левые члены одинаковы.

$ R_A + R_B = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $ Уравнение 1

$ R_B + R_C = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $ Уравнение 2

$ R_C + R_A = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $ Уравнение 3

Добавив три приведенных выше уравнения, мы получим

$$ 2 (R_A + R_B + R_C) = \ frac {2 (R_1 R_2 + R_2 R_3 + R_3 R_1)} {R_1 + R_2 + R_3} $$

$ \ Rightarrow R_A + R_B + R_C = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} $ Уравнение 4

Вычтите уравнение 2 из уравнения 4.

$ R_A + R_B + R_C — (R_B + R_C) = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} — \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $

$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$

Вычитая уравнение 3 из уравнения 4, мы получим

$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$

Вычитая уравнение 1 из уравнения 4, мы получим

$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$

Используя приведенные выше соотношения, мы можем найти сопротивления звездной сети из сопротивлений дельта-сети. Таким образом, мы можем преобразовать дельта-сеть в звездную сеть .

пример

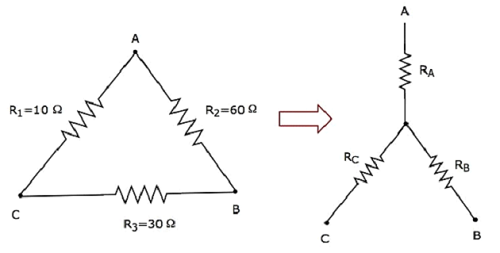
Рассчитаем сопротивления звездной сети , которые эквивалентны сопротивлению дельта-сети, как показано на следующем рисунке.

Учитывая сопротивления дельта сети как R ₁ = 10 Ом, R ₂ = 60 Ом и R ₃ = 30 Ом.

Нам известны следующие соотношения сопротивлений звездной сети в терминах сопротивлений дельта-сети.

$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$

$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$

$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$

Подставим значения R ₁ , R ₂ и R ₃ в приведенные выше уравнения.

$$ R_A = \ frac {10 \ times 60} {10 + 60 + 30} = \ frac {600} {100} = 6 \ Omega $$

$$ R_B = \ frac {60 \ times 30} {10 + 60 + 30} = \ frac {1800} {100} = 18 \ Omega $$

$$ R_C = \ frac {30 \ times 10} {10 + 60 + 30} = \ frac {300} {100} = 3 \ Omega $$

Итак, мы получили сопротивления звездной сети как R _A = 6 Ом, R _B = 18 Ом; и R _C = 3 Ом; , которые эквивалентны сопротивлениям данной дельта-сети.

Теория сети — преобразование звезды в дельту

В предыдущей главе мы обсуждали преобразование дельта-сети в эквивалентную звездную сеть. Теперь давайте поговорим о преобразовании звездной сети в эквивалентную дельта-сеть. Это преобразование называется преобразованием звезды в дельту .

В предыдущей главе мы получили сопротивления звездной сети от сети дельта как

$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ Уравнение 1

$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ Уравнение 2

$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ Уравнение 3

Сопротивления сети Delta с точки зрения сопротивления сети Star

Давайте манипулируем вышеприведенными уравнениями, чтобы получить сопротивления дельта-сети в терминах сопротивлений звездной сети.

• Умножьте каждый набор из двух уравнений, а затем сложите .

Умножьте каждый набор из двух уравнений, а затем сложите .

$$ R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 ^ 2 R_3 + R_2 R_3 ^ 2 R_1 + R_3 R_1 ^ 2 R_2} {(R_1 + R_2 + R_3) ^ 2} $$

$$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3 (R_1 + R_2 + R_3)} {(R_1 + R_2 + R_3) ^ 2} $$

$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3} {R_1 + R_2 + R_3} $ Уравнение 4

• Разделив Уравнение 4 на Уравнение 2, мы получим

Разделив Уравнение 4 на Уравнение 2, мы получим

$$ \ frac {R_A R_B + R_B R_C + R_C R_A} {R_B} = R_1 $$

$$ \ Rightarrow R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$

• Разделив Уравнение 4 на Уравнение 3, мы получим

Разделив Уравнение 4 на Уравнение 3, мы получим

$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$

• Разделив Уравнение 4 на Уравнение 1, мы получим

Разделив Уравнение 4 на Уравнение 1, мы получим

$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$

Используя приведенные выше соотношения, мы можем найти сопротивления дельта-сети из сопротивлений звездной сети. Таким образом, мы можем преобразовать звездную сеть в дельта-сеть .

пример

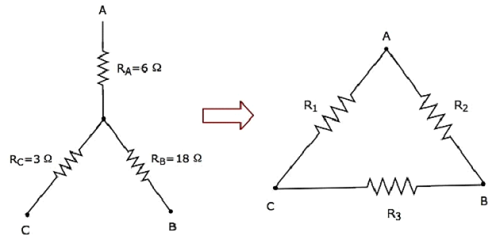
Рассчитаем сопротивления дельта-сети , которые эквивалентны сопротивлению звездной сети, как показано на следующем рисунке.

Учитывая сопротивление звездной сети как R _A = 6 Ом, R _B = 18 Ом; и R _C = 3 Ом; ,

Нам известны следующие соотношения сопротивлений дельта-сети в терминах сопротивлений звездной сети.

$$ R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$

$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$

$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$

Подставим значения R _A , R _B и R _C в приведенные выше уравнения.

$$ R_1 = 3 + 6 + \ frac {3 \ times 6} {18} = 9 + 1 = 10 \ Omega $$

$$ R_2 = 6 + 18 + \ frac {6 \ times 18} {3} = 24 + 36 = 60 \ Omega $$

$$ R_3 = 18 + 3 + \ frac {18 \ times 3} {6} = 21 + 9 = 30 \ Omega $$

Итак, мы получили сопротивления дельта сети как R ₁ = 10 Ом, R ₂ = 60 Ом; и R ₃ = 30 Ом; , которые эквивалентны сопротивлениям данной звездной сети.

Теория сети — топология сети

Топология сети — это графическое представление электрических цепей. Это полезно для анализа сложных электрических цепей путем преобразования их в сетевые графы. Топология сети также называется теорией графов .

Основная терминология топологии сети

Теперь давайте поговорим об основной терминологии этой топологии сети.

график

Сетевой граф просто называется графом . Он состоит из набора узлов, соединенных ветвями. В графах узел является общей точкой двух или более ветвей. Иногда только одна ветвь может подключаться к узлу. Ветвь — это отрезок, соединяющий два узла.

Любую электрическую цепь или сеть можно преобразовать в ее эквивалентный график , заменив пассивные элементы и источники напряжения короткими замыканиями, а источники тока — разомкнутыми. Это означает, что линейные сегменты на графике представляют ветви, соответствующие либо пассивным элементам, либо источникам напряжения электрической цепи.

пример

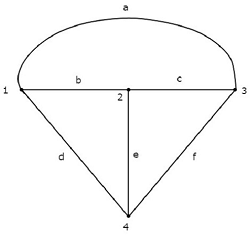
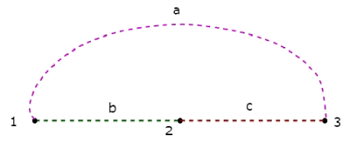
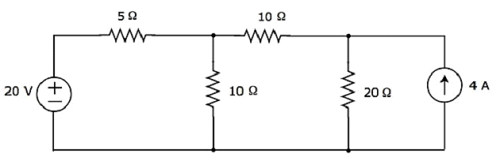
Рассмотрим следующую электрическую цепь .

В вышеупомянутой схеме есть четыре главных узла, и те отмечены как 1, 2, 3 и 4. В вышеупомянутой схеме есть семь ветвей , среди которых одна ветвь содержит источник напряжения 20 В, другая ветвь содержит 4 А Источник тока и остальные пять ответвлений содержат резисторы с сопротивлениями 30 Ом, 5 Ом, 10 Ом, 10 Ом и 20 Ом соответственно.

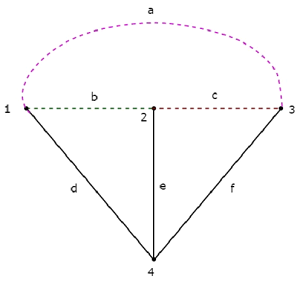
Эквивалентный график, соответствующий вышеуказанной электрической цепи, показан на следующем рисунке.

На приведенном выше графике есть четыре узла, и они помечены 1, 2, 3 и 4 соответственно. Они такие же, как у основных узлов в электрической цепи. На приведенном выше графике есть шесть ветвей, которые помечены как a, b, c, d, e & f соответственно.

В этом случае на графике мы получили на одну ветвь меньше, потому что источник тока 4 А выполнен в виде разомкнутой цепи, при этом преобразовывая электрическую цепь в эквивалентный график.

Из этого примера мы можем сделать следующие выводы:

• Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.

• Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.

Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.

Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.

Типы графиков

Ниже приведены типы графиков —

• Связанный график
• Неподключенный график
• Направленный граф
• Ненаправленный граф

Теперь давайте обсудим эти графики один за другим.

Связанный график

Если существует хотя бы одна ветвь между любыми двумя узлами графа, то она называется связным графом . Это означает, что каждый узел в связанном графе будет иметь одну или несколько ветвей, которые связаны с ним. Таким образом, ни один узел не будет представлен как изолированный или разделенный.

График, показанный в предыдущем примере, является связным графом . Здесь все узлы связаны тремя ветвями.

Неподключенный график

Если в графе существует хотя бы один узел, который не связан даже одной ветвью, то он называется несвязанным графом . Таким образом, в несвязном графе будет один или несколько изолированных узлов.

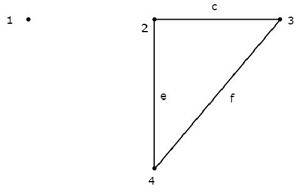
Рассмотрим график, показанный на следующем рисунке.

На этом графике узлы 2, 3 и 4 соединены двумя ветвями каждый. Но ни одна ветвь не была подключена к узлу 1 . Таким образом, узел 1 становится изолированным узлом . Следовательно, приведенный выше граф является несвязным графом .

Направленный граф

Если все ветви графа представлены стрелками, то этот граф называется ориентированным графом . Эти стрелки указывают направление протекания тока в каждой ветви. Следовательно, этот граф также называется ориентированным графом .

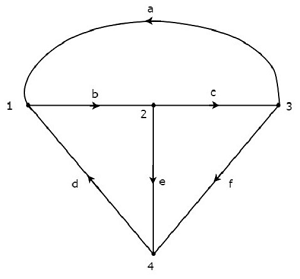
Рассмотрим график, показанный на следующем рисунке.

На приведенном выше графике направление потока тока обозначено стрелкой в ​​каждой ветви. Следовательно, это ориентированный граф .

Ненаправленный граф

Если ветви графа не представлены стрелками, то этот граф называется неориентированным графом . Поскольку нет направления потока тока, этот граф также называется неориентированным графом .

График, показанный в первом примере этой главы, является неориентированным графом , поскольку на ветвях этого графа нет стрелок.

Подграф и его виды

Часть графа называется подграфом . Мы получаем подграфы, удаляя некоторые узлы и / или ветви данного графа. Таким образом, количество ветвей и / или узлов подграфа будет меньше, чем у исходного графа. Отсюда можно сделать вывод, что подграф является подмножеством графа.

Ниже приведены два типа подграфов.

• дерево
• Co-Tree

дерево

Дерево является связным подграфом данного графа, который содержит все узлы графа. Но в этом подграфе не должно быть петель. Ветви дерева называются ветками .

Рассмотрим следующий связанный подграф графа, который показан в Примере начала этой главы.

Этот связанный подграф содержит все четыре узла данного графа и петли нет. Следовательно, это Дерево .

Это дерево имеет только три ветви из шести ветвей данного графа. Потому что, если мы рассмотрим хотя бы одну ветвь из оставшихся ветвей графа, то в вышеуказанном подграфе будет цикл. Тогда результирующий связанный подграф не будет деревом.

Из вышеприведенного дерева мы можем сделать вывод, что количество ветвей , которые присутствуют в дереве, должно быть равно n — 1, где «n» — количество узлов данного графа.

Co-Tree

Co-Tree — это подграф, который состоит из ветвей, которые удаляются при формировании дерева. Следовательно, это называется дополнением дерева. Для каждого дерева будет соответствующее Co-Tree, и его ветви называются ссылками или аккордами. В общем, ссылки представлены пунктирными линиями.

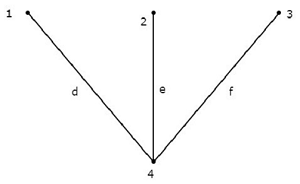
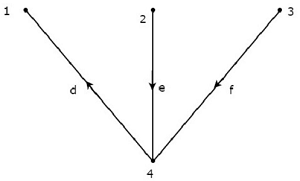
Co-Tree, соответствующее вышеуказанному дереву, показано на следующем рисунке.

Это Co-Tree имеет только три узла вместо четырех узлов данного графа, потому что Узел 4 изолирован от вышеуказанного Co-Tree. Следовательно, Co-Tree не обязательно должен быть связанным подграфом. Это Co-Tree имеет три ветви, и они образуют петлю.

Количество ветвей , присутствующих в совместном дереве, будет равно разнице между количеством ветвей данного графа и количеством веток. Математически это можно записать как

$$ l = b — (n — 1) $$

$$ l = b — n + 1 $$

Куда,

• л количество ссылок.
• b — количество ветвей, присутствующих в данном графике.
• n — количество узлов, присутствующих в данном графе.

Если мы объединим дерево и соответствующее ему Co-дерево, мы получим исходный граф, как показано ниже.

Ветви дерева d, e & f представлены сплошными линиями. Ветви Co-Tree a, b & c представлены пунктирными линиями.

Матрицы топологии сети

В предыдущей главе мы обсуждали, как преобразовать электрическую цепь в эквивалентный граф. Теперь давайте обсудим Матрицы топологии сети, которые полезны для решения любой проблемы электрической цепи или сети с использованием их эквивалентных графов.

Матрицы, связанные с сетевыми графами

Ниже приведены три матрицы, которые используются в теории графов.

• Матрица заболеваемости
• Матрица фундаментальной петли
• Фундаментальный крой Set Matrix

Матрица заболеваемости

Матрица инцидентности представляет график данной электрической цепи или сети. Следовательно, можно нарисовать график той же электрической цепи или сети из матрицы инцидентности .

Мы знаем, что граф состоит из множества узлов, которые связаны между собой несколькими ветвями. Итак, соединение ветвей с узлом называется инцидентностью. Матрица инцидентности представлена ​​буквой А. Она также называется матрицей инцидентности между узлами или матрицей узлов .

Если в ориентированном графе имеется «n» узлов и «b» ответвлений, то матрица инцидентности будет иметь «n» строк и «b» столбцов. Здесь строки и столбцы соответствуют узлам и ветвям ориентированного графа. Следовательно, порядок матрицы инцидентности будет n × b .

Элементы матрицы инцидентности будут иметь одно из этих трех значений: +1, -1 и 0.

• Если ток ветви уходит из выбранного узла, то значение элемента будет +1.

• Если ток ветви поступает в направлении выбранного узла, то значение элемента будет равно -1.

• Если ток ветви не входит в выбранный узел и не выходит из выбранного узла, тогда значение элемента будет 0.

Если ток ветви уходит из выбранного узла, то значение элемента будет +1.

Если ток ветви поступает в направлении выбранного узла, то значение элемента будет равно -1.

Если ток ветви не входит в выбранный узел и не выходит из выбранного узла, тогда значение элемента будет 0.

Процедура поиска Матрицы заболеваемости

Выполните следующие действия, чтобы найти матрицу инцидентности ориентированного графа.

• Выберите узел во время данного ориентированного графа и заполните значения элементов матрицы инцидентности, соответствующих этому узлу, в строке.

• Повторите вышеуказанный шаг для всех узлов данного ориентированного графа.

Выберите узел во время данного ориентированного графа и заполните значения элементов матрицы инцидентности, соответствующих этому узлу, в строке.

Повторите вышеуказанный шаг для всех узлов данного ориентированного графа.

пример

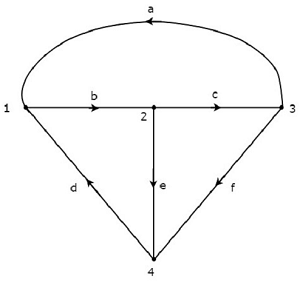
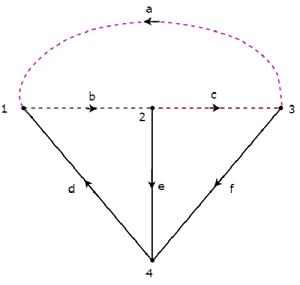
Рассмотрим следующий ориентированный граф .

Матрица инцидентности, соответствующая приведенному выше ориентированному графу, будет

$$ A = \ begin {bmatrix} -1 & 1 & 0 & -1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 & -1 \ end {bmatrix} $$

Строки и столбцы вышеприведенной матрицы представляют узлы и ветви данного ориентированного графа. Порядок этой матрицы инцидентности составляет 4 × 6.

Соблюдая приведенную выше матрицу инцидентности, можно сделать вывод, что сумма элементов столбца матрицы инцидентности равна нулю. Это означает, что ток ветвления выходит из одного узла и входит только в другой отдельный узел.

Примечание. Если данный граф является неориентированным типом, преобразуйте его в ориентированный граф, представив стрелки на каждой его ветви. Мы можем рассмотреть произвольное направление протекания тока в каждой ветви.

Матрица фундаментальной петли

Фундаментальный цикл или f-цикл представляет собой цикл, который содержит только одну ссылку и одну или несколько веток. Итак, количество f-циклов будет равно количеству ссылок. Матрица фундаментальной петли представлена ​​буквой B. Она также называется матрицей фундаментальной цепи и матрицей Tie-set. Эта матрица дает соотношение между токами ветвления и токами звеньев.

Если в ориентированном графе имеется n узлов и ветви b присутствуют, то количество ссылок, присутствующих в совместном дереве, которое соответствует выбранному дереву данного графа, будет b-n + 1.

Таким образом, матрица основного цикла будет иметь строки «b-n + 1» и столбцы «b». Здесь строки и столбцы соответствуют ссылкам co-дерева и ветвей данного графа. Следовательно, порядок матрицы фундаментального цикла будет (b — n + 1) × b .

Элементы матрицы основного цикла будут иметь одно из этих трех значений: +1, -1 и 0.

• Значение элемента будет +1 для ссылки выбранного f-цикла.

• Значение элементов будет равно 0 для остальных ссылок и веток, которые не являются частью выбранного f-цикла.

• Если направление тока ветки выбранного f-контура совпадает с направлением тока линии f-контура, то значение элемента будет +1.

• Если направление тока ветки выбранного f-петли противоположно направлению тока звена f-петли, тогда значение элемента будет -1.

Значение элемента будет +1 для ссылки выбранного f-цикла.

Значение элементов будет равно 0 для остальных ссылок и веток, которые не являются частью выбранного f-цикла.

Если направление тока ветки выбранного f-контура совпадает с направлением тока линии f-контура, то значение элемента будет +1.

Если направление тока ветки выбранного f-петли противоположно направлению тока звена f-петли, тогда значение элемента будет -1.

Процедура поиска матрицы фундаментальных циклов

Выполните следующие шаги, чтобы найти матрицу фундаментального цикла данного ориентированного графа.

• Выберите дерево заданного ориентированного графа.

• Включая одну ссылку за раз, мы получим один f-цикл. Заполните значения элементов, соответствующих этому f-циклу, в строке матрицы фундаментального цикла.

• Повторите вышеуказанный шаг для всех ссылок.

Выберите дерево заданного ориентированного графа.

Включая одну ссылку за раз, мы получим один f-цикл. Заполните значения элементов, соответствующих этому f-циклу, в строке матрицы фундаментального цикла.

Повторите вышеуказанный шаг для всех ссылок.

пример

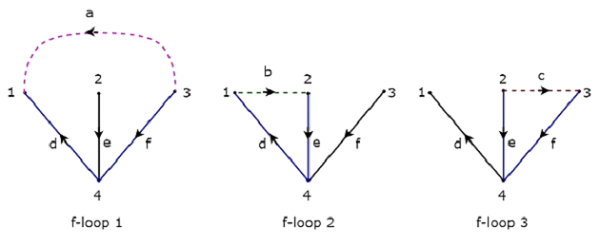
Взгляните на следующее дерево ориентированного графа , которое рассматривается для матрицы инцидентности.

Вышеуказанное дерево содержит три ветви d, e & f. Следовательно, ветви a, b & c будут связями Co-Tree, соответствующими вышеуказанному дереву. Включая одну ссылку за раз на вышеуказанное дерево, мы получим один f-цикл . Таким образом, будет три f-петли , так как есть три ссылки. Эти три f-петли показаны на следующем рисунке.

На рисунке выше ветви, которые представлены цветными линиями, образуют f-петли. Мы получим значения построчных элементов матрицы Tie-set из каждого f-цикла. Таким образом, матрица Tieset рассмотренного выше дерева будет

$$ B = \ begin {bmatrix} 1 & 0 & 0 & -1 & 0 & -1 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & -1 & 1 \ конец {bmatrix} $$

Строки и столбцы вышеприведенной матрицы представляют собой связи и ветви данного ориентированного графа. Порядок этой матрицы инцидентности составляет 3 × 6.

Количество матриц основного цикла ориентированного графа будет равно количеству деревьев этого ориентированного графа. Потому что каждое дерево будет иметь одну матрицу фундаментальных циклов.

Фундаментальная обрезная матрица

Фундаментальный набор срезов или набор f-срезов — это минимальное количество ветвей, которые удаляются из графа таким образом, что исходный граф станет двумя изолированными подграфами. Набор f-cut содержит только одну веточку и одну или несколько ссылок. Таким образом, количество наборов f-cut будет равно количеству веточек.

Матрица набора основных срезов обозначена буквой C. Эта матрица дает соотношение между напряжениями ответвления и напряжениями ветки.

Если в ориентированном графе имеется «n» узлов и «b» ветвей, то количество веток в выбранном дереве данного графа будет n-1. Таким образом, матрица основного набора сокращений будет иметь n-1 строки и столбцы b. Здесь строки и столбцы соответствуют веткам выбранного дерева и ветвям данного графа. Следовательно, порядок матрицы базового набора сечений будет (n-1) × b .

Элементы матрицы набора базовых сечений будут иметь одно из этих трех значений: +1, -1 и 0.

• Значение элемента будет +1 для ветки выбранного f-cutset.

• Значение элементов будет 0 для оставшихся веток и ссылок, которые не являются частью выбранного f-cutset.

• Если направление тока связи выбранного набора f-отрезков такое же, как и у потока веток f-отрезков, то значение элемента будет +1.

• Если направление тока связи выбранного набора f-cut противоположно направлению тока ветки f-cutset, то значение элемента будет -1.

Значение элемента будет +1 для ветки выбранного f-cutset.

Значение элементов будет 0 для оставшихся веток и ссылок, которые не являются частью выбранного f-cutset.

Если направление тока связи выбранного набора f-отрезков такое же, как и у потока веток f-отрезков, то значение элемента будет +1.

Если направление тока связи выбранного набора f-cut противоположно направлению тока ветки f-cutset, то значение элемента будет -1.

Процедура нахождения Фундаментальной Вырезанной Матрицы

Выполните следующие шаги, чтобы найти матрицу фундаментальных наборов сечений данного ориентированного графа.

• Выберите дерево заданного ориентированного графа и представьте ссылки пунктирными линиями.

• Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Заполните значения элементов, соответствующих этому набору f-сечений, в строке основной матрицы срезов.

• Повторите вышеуказанный шаг для всех веток.

Выберите дерево заданного ориентированного графа и представьте ссылки пунктирными линиями.

Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Заполните значения элементов, соответствующих этому набору f-сечений, в строке основной матрицы срезов.

Повторите вышеуказанный шаг для всех веток.

пример

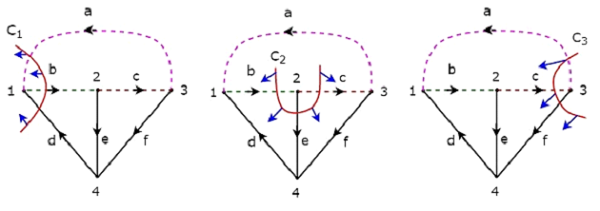
Рассмотрим тот же ориентированный граф , который мы обсуждали в разделе матрицы инцидентности. Выберите ветви d, e & f этого ориентированного графа в виде веточек. Таким образом, оставшиеся ветви a, b & c этого ориентированного графа будут ссылками.

Веточки d, e & f представлены сплошными линиями, а ссылки a, b и c представлены пунктирными линиями на следующем рисунке.

Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Итак, будет три набора f-cut, так как есть три веточки. Эти три набора f-cut показаны на следующем рисунке.

У нас будет три набора f-cut, удалив набор веток и звеньев C ₁ , C ₂ и C ₃ . Мы получим значения построчных элементов матрицы фундаментальных наборов сечений из каждого набора f-срезов. Таким образом, основная матрица множества срезов рассмотренного выше дерева будет

$$ C = \ begin {bmatrix} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \ конец {bmatrix} $$

Строки и столбцы вышеприведенной матрицы представляют собой веточки и ветви данного ориентированного графа. Порядок этой основной матрицы сечений равен 3 × 6.

Количество матриц Фундаментального набора сечений ориентированного графа будет равно количеству деревьев этого ориентированного графа. Потому что каждое дерево будет иметь одну матрицу Фундаментального среза.

Теория сетей — теорема суперпозиции

Теорема о суперпозиции основана на понятии линейности между откликом и возбуждением электрической цепи. В нем говорится, что отклик в конкретной ветви линейного контура, когда несколько независимых источников действуют одновременно, эквивалентен сумме откликов, связанных с каждым независимым источником, действующим одновременно.

В этом методе мы будем рассматривать только один независимый источник за один раз. Итак, мы должны исключить оставшиеся независимые источники из схемы. Мы можем устранить источники напряжения, замкнув их две клеммы и, аналогично, источники тока, открыв их две клеммы.

Следовательно, нам нужно найти ответ в определенной ветке «n» раз, если существует «n» независимых источников. Ответом в конкретной ветви может быть либо ток, протекающий через эту ветвь, либо напряжение через эту ветвь.

Процедура теоремы суперпозиции

Выполните следующие шаги, чтобы найти ответ в конкретной ветви, используя теорему суперпозиции.

Шаг 1 — Найти ответ в конкретной ветви, рассмотрев один независимый источник и исключив оставшиеся независимые источники, присутствующие в сети.

Шаг 2 — Повторите Шаг 1 для всех независимых источников, присутствующих в сети.

Шаг 3 — Добавьте все ответы, чтобы получить общий ответ в конкретной ветви, когда все независимые источники присутствуют в сети.

пример

Найти ток, протекающий через резистор 20 Ом следующей цепи, используя теорему суперпозиции .

Шаг 1 — Найдем ток, протекающий через резистор 20 Ом, с учетом только источника напряжения 20 В. В этом случае мы можем устранить источник тока 4 А, разомкнув его. Модифицированная принципиальная схема показана на следующем рисунке.

В вышеуказанной цепи есть только один главный узел, кроме Земли. Итак, мы можем использовать метод узлового анализа . Узел напряжения V ₁ обозначен на следующем рисунке. Здесь V ₁ — это напряжение от узла 1 относительно земли.

Узловое уравнение в узле 1

$$ \ frac {V_1 — 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$

$$ \ Rightarrow \ frac {6V_1 — 120 + 3V_1 + V_1} {30} = 0 $$

$$ \ Rightarrow 10V_1 = 120 $$

$$ \ Rightarrow V_1 = 12V $$

Ток, протекающий через резистор 20 Ом, можно найти, выполнив следующее упрощение.

$$ I_1 = \ frac {V_1} {10 + 20} $$

Подставим значение V ₁ в приведенное выше уравнение.

$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A $$

Следовательно, ток, протекающий через резистор 20 Ом, составляет 0,4 А , если рассматривать только источник напряжения 20 В.

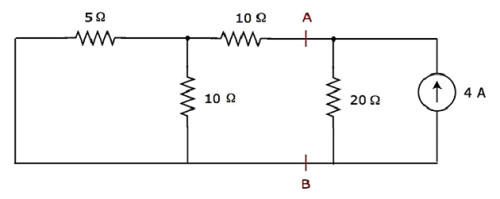
Шаг 2 — Давайте найдем ток, протекающий через резистор 20 Ом, рассматривая только источник тока 4 А. В этом случае мы можем устранить источник напряжения 20 В, сделав его коротким замыканием. Модифицированная принципиальная схема показана на следующем рисунке.

В приведенной выше схеме есть три резистора слева от клемм A и B. Мы можем заменить эти резисторы одним эквивалентным резистором . Здесь резисторы 5 Ом и 10 Ом подключены параллельно, и вся комбинация последовательно соединена с резистором 10 Ом.

Эквивалентное сопротивление слева от клемм A и B будет

$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$

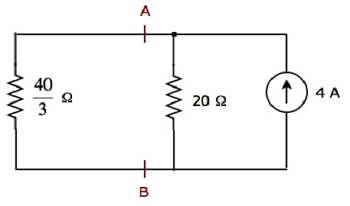
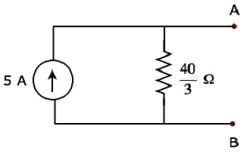
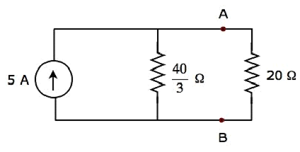
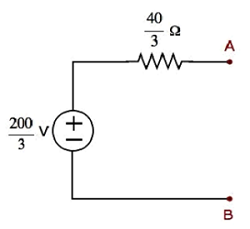
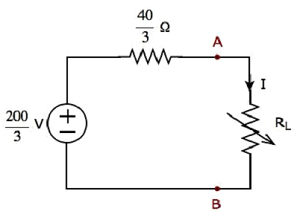
Упрощенная принципиальная схема показана на следующем рисунке.

Мы можем найти ток, протекающий через резистор 20 Ом, используя принцип деления тока .

$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$

Замените $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ и $ R_2 = 20 \ Omega $ в вышеприведенном уравнении.

$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1.6 А $$

Следовательно, ток, протекающий через резистор 20 Ом, составляет 1,6 А , если рассматривать только источник тока 4 А.

Шаг 3 — Мы получим ток, протекающий через резистор 20 Ом данной цепи, сложив два тока, которые мы получили на шаге 1 и шаге 2. Математически это можно записать как

$$ I = I_1 + I_2 $$

Подставим значения I ₁ и I ₂ в приведенное выше уравнение.

$$ I = 0,4 + 1,6 = 2 A $$

Следовательно, ток, протекающий через резистор 20 Ом данной цепи, составляет 2 А.

Примечание. Мы не можем напрямую применить теорему о суперпозиции, чтобы определить количество энергии, подаваемой на любой резистор, присутствующий в линейной цепи, просто добавляя мощности, подаваемые на этот резистор из-за каждого независимого источника. Скорее, мы можем рассчитать либо общий ток, протекающий через этот резистор, либо напряжение на нем, используя теорему суперпозиции, и исходя из этого, мы можем рассчитать количество энергии, подаваемой на этот резистор, используя $ I ^ 2 R $ или $ \ frac {V ^ 2} {R} $.

Теория сетей — теорема Тевенина

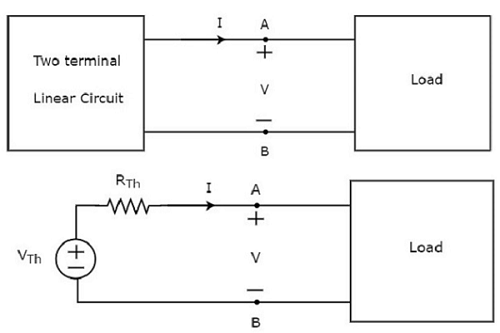
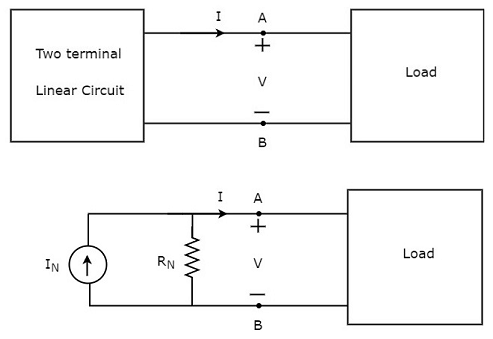
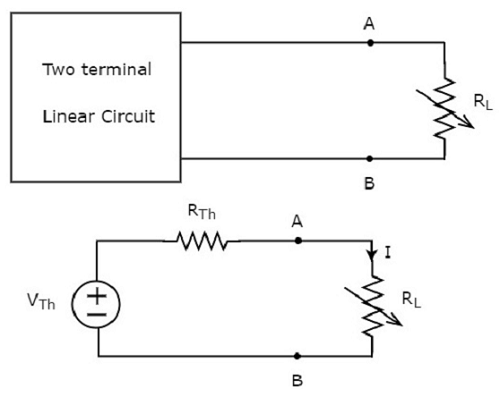
Теорема Тевенина утверждает, что любые двухполюсные линейные сеть или цепь могут быть представлены эквивалентной сетью или схемой, которая состоит из источника напряжения, включенного последовательно с резистором. Он известен как эквивалентная схема Тевенина. Линейная цепь может содержать независимые источники, зависимые источники и резисторы.

Если схема содержит несколько независимых источников, зависимых источников и резисторов, то отклик в элементе можно легко найти, заменив всю сеть слева от этого элемента эквивалентной схемой Тевенина .

Отклик в элементе может быть напряжением на этом элементе, током, протекающим через этот элемент, или мощностью, рассеиваемой на этом элементе.

Эта концепция проиллюстрирована на следующих рисунках.

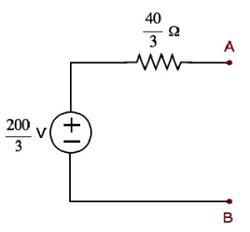
Эквивалентная схема Тевенина напоминает практический источник напряжения. Следовательно, он имеет источник напряжения последовательно с резистором.

• Источник напряжения, присутствующий в эквивалентной цепи Тевенина, называется эквивалентным напряжением Тевенина или просто напряжением Тевенина, V _Th .

• Резистор, присутствующий в эквивалентной схеме Тевенина, называется эквивалентным резистором Тевенина или просто резистором Тевенина, R _Th .

Источник напряжения, присутствующий в эквивалентной цепи Тевенина, называется эквивалентным напряжением Тевенина или просто напряжением Тевенина, V _Th .

Резистор, присутствующий в эквивалентной схеме Тевенина, называется эквивалентным резистором Тевенина или просто резистором Тевенина, R _Th .

Методы нахождения эквивалентной схемы Тевенина

Есть три способа найти эквивалентную схему Тевенина. В зависимости от типа источников , присутствующих в сети, мы можем выбрать один из этих трех методов. Теперь давайте обсудим два метода один за другим. Мы обсудим третий метод в следующей главе.

Способ 1

Выполните следующие действия, чтобы найти эквивалентную схему Тевенина, когда присутствуют только источники независимого типа .

• Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Thevenin.

• Шаг 2 — Найти напряжение Тевенина V _Th на разомкнутых клеммах вышеуказанной цепи.

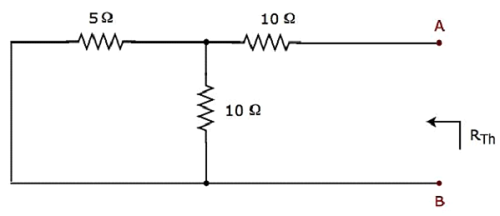
• Шаг 3 — Найти сопротивление Тевенина R _Th через открытые клеммы вышеупомянутой цепи, устранив независимые источники, присутствующие в ней.

• Шаг 4 — Нарисуйте эквивалентную схему Тевенина, соединив напряжение Тевенина V _Th последовательно с сопротивлением Тевенина R _Th .

Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Thevenin.

Шаг 2 — Найти напряжение Тевенина V _Th на разомкнутых клеммах вышеуказанной цепи.

Шаг 3 — Найти сопротивление Тевенина R _Th через открытые клеммы вышеупомянутой цепи, устранив независимые источники, присутствующие в ней.

Шаг 4 — Нарисуйте эквивалентную схему Тевенина, соединив напряжение Тевенина V _Th последовательно с сопротивлением Тевенина R _Th .

Теперь мы можем найти ответ в элементе, который находится справа от эквивалентной схемы Тевенина.

пример

Найдите ток, протекающий через резистор 20 Ом, сначала найдя эквивалентную цепь Thevenin слева от клемм A и B.

Шаг 1 — Чтобы найти эквивалентную схему Thevenin с левой стороны клемм A и B, мы должны удалить резистор 20 Ом из сети, открыв клеммы A и B. Модифицированная принципиальная схема показана на следующем рисунке.

Шаг 2 — Расчет напряжения Тевенина V _Th .

В вышеуказанной цепи есть только один главный узел, кроме Земли. Итак, мы можем использовать метод узлового анализа . Напряжение узла V ₁ и напряжение Тевенина V _Th обозначены на рисунке выше. Здесь V ₁ — это напряжение от узла 1 относительно земли, а V _Th — это напряжение на источнике тока 4 А.

• Узловое уравнение в узле 1

Узловое уравнение в узле 1

$$ \ frac {V_1 — 20} {5} + \ frac {V_1} {10} — 4 = 0 $$

$$ \ Rightarrow \ frac {2V_1 — 40 + V_1 — 40} {10} = 0 $$

$$ \ Rightarrow 3V_1 — 80 = 0 $$

$$ \ Rightarrow V_1 = \ frac {80} {3} V $$

• Напряжение на резисторе 10 Ом

Напряжение на резисторе 10 Ом

$$ V_ {10 \ Omega} = (-4) (10) = -40 В $$

• В приведенной выше схеме есть две сетки. Уравнение КВЛ вокруг второй сетки

В приведенной выше схеме есть две сетки. Уравнение КВЛ вокруг второй сетки

$$ V_1 — V_ {10 \ Omega} — V_ {Th} = 0 $$

• Подставьте значения $ V_1 $ и $ V_ {10 \ Omega} $ в вышеприведенном уравнении.

Подставьте значения $ V_1 $ и $ V_ {10 \ Omega} $ в вышеприведенном уравнении.

$$ \ frac {80} {3} — (-40) — V_ {Th} = 0 $$

$$ V_ {Th} = \ frac {80 + 120} {3} = \ frac {200} {3} V $$

• Поэтому напряжение Тевенина составляет $ V_ {Th} = \ frac {200} {3} V $

Поэтому напряжение Тевенина составляет $ V_ {Th} = \ frac {200} {3} V $

Шаг 3 — Расчет сопротивления Тевенина R _Th .

Замкните короткое замыкание источника напряжения и разомкните источник тока вышеуказанной цепи, чтобы рассчитать сопротивление Тевенина R _Th на клеммах A и B. Модифицированная принципиальная схема показана на следующем рисунке.

Сопротивление Thevenin через терминалы A & B будет

$$ R_ {Th} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$

Следовательно, сопротивление Тевенина составляет $ \ mathbf {R_ {Th} = \ frac {40} {3} \ Omega} $.

Шаг 4 — Эквивалентная схема Thevenin находится слева от клемм A и B в данной схеме. Эта принципиальная схема показана на следующем рисунке.

Ток, протекающий через резистор 20 Ом, можно найти, подставив значения V _Th , R _Th и R в следующее уравнение.

$$ l = \ frac {V_ {Th}} {R_ {Th} + R} $$

$$ l = \ frac {\ frac {200} {3}} {\ frac {40} {3} + 20} = \ frac {200} {100} = 2A $$

Следовательно, ток, протекающий через резистор 20 Ом, составляет 2 А.

Способ 2

Выполните следующие действия, чтобы найти эквивалентную схему Тевенина, когда присутствуют источники как независимого, так и зависимого типа .

• Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Thevenin.

• Шаг 2 — Найти напряжение Тевенина V _Th на разомкнутых клеммах вышеуказанной цепи.

• Шаг 3 — Найти ток короткого замыкания I _SC , замкнув две разомкнутые клеммы вышеуказанной цепи.

• Шаг 4 — Найти сопротивление Тевенина R _Th с помощью следующей формулы.

Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Thevenin.

Шаг 2 — Найти напряжение Тевенина V _Th на разомкнутых клеммах вышеуказанной цепи.

Шаг 3 — Найти ток короткого замыкания I _SC , замкнув две разомкнутые клеммы вышеуказанной цепи.

Шаг 4 — Найти сопротивление Тевенина R _Th с помощью следующей формулы.

$$ R_ {Th} = \ frac {V_ {Th}} {I_ {SC}} $$

Шаг 5 — Нарисуйте эквивалентную схему Тевенина, соединив напряжение Тевенина V _Th последовательно с сопротивлением Тевенина R _Th .

Теперь мы можем найти ответ в элементе, который находится справа от эквивалентной схемы Тевенина.

Теория сетей — теорема Нортона

Теорема Нортона аналогична теореме Тевенина. В нем говорится, что любые двухполюсные линейные сеть или схема могут быть представлены эквивалентной сетью или схемой, которая состоит из источника тока параллельно с резистором. Он известен как эквивалентная схема Нортона . Линейная цепь может содержать независимые источники, зависимые источники и резисторы.

Если схема имеет несколько независимых источников, зависимых источников и резисторов, то отклик в элементе можно легко найти, заменив всю сеть слева от этого элемента эквивалентной схемой Нортона .

Реакцией в элементе может быть напряжение на этом элементе, ток, протекающий через этот элемент, или мощность, рассеиваемая через этот элемент.

Эта концепция проиллюстрирована на следующих рисунках.

Эквивалентная схема Нортона напоминает практический источник тока. Следовательно, он имеет источник тока параллельно с резистором.

• Источник тока, присутствующий в эквивалентной схеме Нортона, называется эквивалентным током Нортона или просто током Нортона I _N.

• Резистор, присутствующий в эквивалентной схеме Нортона, называется эквивалентным резистором Нортона или просто резистором Нортона R _N.

Источник тока, присутствующий в эквивалентной схеме Нортона, называется эквивалентным током Нортона или просто током Нортона I _N.

Резистор, присутствующий в эквивалентной схеме Нортона, называется эквивалентным резистором Нортона или просто резистором Нортона R _N.

Методы нахождения эквивалентной схемы Нортона

Есть три способа найти эквивалентную схему Нортона. В зависимости от типа источников, присутствующих в сети, мы можем выбрать один из этих трех методов. Теперь давайте обсудим эти три метода один за другим.

Способ 1

Выполните следующие действия, чтобы найти эквивалентную схему Нортона, когда присутствуют только источники независимого типа .

• Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Нортона.

• Шаг 2 — Найти ток Нортона I _N , замкнув два разомкнутых контакта вышеуказанной цепи.

• Шаг 3 — Найти сопротивление Нортона R _N через разомкнутые клеммы цепи, рассмотренной на шаге 1, устраняя независимые источники, присутствующие в нем. Сопротивление Нортона R _N будет таким же, как у сопротивления Тевенина R _Th .

• Шаг 4 — Нарисуйте эквивалентную цепь Нортона, подключив вход IN тока Нортона параллельно с сопротивлением Нортона R _N.

Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Нортона.

Шаг 2 — Найти ток Нортона I _N , замкнув два разомкнутых контакта вышеуказанной цепи.

Шаг 3 — Найти сопротивление Нортона R _N через разомкнутые клеммы цепи, рассмотренной на шаге 1, устраняя независимые источники, присутствующие в нем. Сопротивление Нортона R _N будет таким же, как у сопротивления Тевенина R _Th .

Шаг 4 — Нарисуйте эквивалентную цепь Нортона, подключив вход IN тока Нортона параллельно с сопротивлением Нортона R _N.

Теперь мы можем найти ответ в элементе, который находится справа от эквивалентной схемы Нортона.

Способ 2

Выполните следующие действия, чтобы найти эквивалентную схему Нортона, когда присутствуют источники как независимого, так и зависимого типа .

• Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Нортона.

• Шаг 2 — Найти напряжение разомкнутой цепи V _OC на разомкнутых клеммах вышеуказанной цепи.

• Шаг 3 — Найти ток Нортона I _N , замкнув два разомкнутых контакта вышеуказанной цепи.

• Шаг 4 — Найти сопротивление Нортона R _N , используя следующую формулу.

Шаг 1 — Рассмотрим принципиальную схему, открыв клеммы, относительно которых должна быть найдена эквивалентная схема Нортона.

Шаг 2 — Найти напряжение разомкнутой цепи V _OC на разомкнутых клеммах вышеуказанной цепи.

Шаг 3 — Найти ток Нортона I _N , замкнув два разомкнутых контакта вышеуказанной цепи.

Шаг 4 — Найти сопротивление Нортона R _N , используя следующую формулу.

$$ R_N = \ frac {V_ {OC}} {I_N} $$

• Шаг 5 — Нарисуйте эквивалентную цепь Нортона, соединив ток Нортона I _N параллельно с сопротивлением Нортона R _N.

Шаг 5 — Нарисуйте эквивалентную цепь Нортона, соединив ток Нортона I _N параллельно с сопротивлением Нортона R _N.

Теперь мы можем найти ответ в элементе, который находится справа от эквивалентной схемы Нортона.

Способ 3

Это альтернативный метод для нахождения эквивалентной схемы Нортона.

• Шаг 1 — Найти эквивалентную схему Thevenin между желаемыми двумя терминалами. Мы знаем, что он состоит из источника напряжения Тевенина, V _Th и резистора Тевенина, R _Th .

• Шаг 2 — Примените метод преобразования источника к вышеуказанной эквивалентной схеме Thevenin. Мы получим эквивалентную схему Нортона. Вот,

Шаг 1 — Найти эквивалентную схему Thevenin между желаемыми двумя терминалами. Мы знаем, что он состоит из источника напряжения Тевенина, V _Th и резистора Тевенина, R _Th .

Шаг 2 — Примените метод преобразования источника к вышеуказанной эквивалентной схеме Thevenin. Мы получим эквивалентную схему Нортона. Вот,

Ток Нортона,

$$ I_N = \ frac {V_ {Th}} {R_ {Th}} $$

Сопротивление Нортона,

$$ R_N = R_ {Th} $$

Эта концепция проиллюстрирована на следующем рисунке.

Теперь мы можем найти ответ в элементе, поместив эквивалентную схему Нортона слева от этого элемента.

Примечание. Аналогично, мы можем найти эквивалентную схему Тевенина, сначала найдя эквивалентную схему Нортона, а затем применив к ней технику преобразования источника. Эта концепция проиллюстрирована на следующем рисунке.

Это метод 3 для нахождения эквивалентной схемы Тевенина.

пример

Найдите ток, протекающий через резистор 20 Ом, сначала найдя эквивалентную цепь Нортона слева от клемм A и B.

Давайте решим эту проблему, используя метод 3 .

Шаг 1 — В предыдущей главе мы вычислили эквивалентную схему Thevenin слева от клемм A и B. Теперь мы можем использовать эту схему. Это показано на следующем рисунке.

Здесь напряжение Тевенина, $ V_ {Th} = \ frac {200} {3} V $, и сопротивление Тевенина, $ R_ {Th} = \ frac {40} {3} \ Omega $

Шаг 2 — Примените метод преобразования источника к вышеуказанной эквивалентной схеме Thevenin. Подставьте значения V _Th и R _Th в следующую формулу тока Нортона .

$$ I_N = \ frac {V_ {Th}} {R_ {Th}} $$

$$ I_N = \ frac {\ frac {200} {3}} {\ frac {40} {3}} = 5A $$

Следовательно, ток Нортона I _N составляет 5 А.

Мы знаем, что сопротивление Нортона, R _N такое же, как сопротивление Тевенина R _Th .

$$ \ mathbf {R_N = \ frac {40} {3} \ Omega} $$

Эквивалентная схема Нортона, соответствующая приведенной выше эквивалентной схеме Тевенина, показана на следующем рисунке.

Теперь поместите эквивалентную схему Нортона слева от клемм A и B данной цепи.

Используя принцип деления тока , ток, протекающий через резистор 20 Ом, будет

$$ I_ {20 \ Omega} = 5 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup $$

$$ I_ {20 \ Omega} = 5 \ lgroup \ frac {40} {100} \ rgroup = 2A $$

Следовательно, ток, протекающий через резистор 20 Ом, составляет 2 А.

Теорема о передаче максимальной мощности

Количество энергии, получаемой нагрузкой, является важным параметром в электрических и электронных приложениях. В цепях постоянного тока мы можем представить нагрузку с резистором, имеющим сопротивление R _L Ом. Точно так же в цепях переменного тока мы можем представить его со сложной нагрузкой, имеющей полное сопротивление Z _L Ом.

Теорема о максимальной передаче мощности гласит, что источник постоянного напряжения будет подавать максимальную мощность на резистор переменной нагрузки только тогда, когда сопротивление нагрузки равно сопротивлению источника.

Аналогично, в теореме о максимальной передаче мощности утверждается, что источник переменного напряжения будет поставлять максимальную мощность для переменной комплексной нагрузки только тогда, когда полное сопротивление нагрузки равно комплексному сопряжению полного сопротивления источника.

В этой главе мы обсудим теорему о максимальной передаче мощности для цепей постоянного тока.

Доказательство теоремы о передаче максимальной мощности

Замените любые двухполюсные линейные сети или цепи на левой стороне резистора с переменной нагрузкой, имеющего сопротивление R _L Ом, эквивалентной цепью Тевенина. Мы знаем, что эквивалентная схема Тевенина напоминает практический источник напряжения.

Эта концепция проиллюстрирована на следующих рисунках.

Количество мощности, рассеиваемой на нагрузочном резисторе, составляет

$$ P_L = I ^ 2 R_L $$

Замените $ I = \ frac {V_ {Th}} {R_ {Th} + R_L} $ в приведенном выше уравнении.

$$ P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L $$

$ \ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L) ^ 2} \ rbrace $ Уравнение 1

Условие для максимальной передачи мощности

Для максимума или минимума первая производная будет равна нулю. Итак, дифференцируем уравнение 1 относительно R _L и сделаем его равным нулю.

$$ \ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L) ^ 2 \ times 1 — R_L \ times 2 (R_ {Th} + R_L) } {(R_ {Th} + R_L) ^ 4} \ rbrace = 0 $$

$$ \ Rightarrow (R_ {Th} + R_L) ^ 2 -2R_L (R_ {Th} + R_L) = 0 $$

$$ \ Rightarrow (R_ {Th} + R_L) (R_ {Th} + R_L — 2R_L) = 0 $$

$$ \ Rightarrow (R_ {Th} — R_L) = 0 $$

$$ \ Rightarrow R_ {Th} = R_L \: или \: R_L = R_ {Th} $$

Следовательно, условием максимального рассеивания мощности на нагрузке является $ R_L = R_ {Th} $. Это означает, что если значение сопротивления нагрузки равно значению сопротивления источника, т. Е. Сопротивления Тевенина, то мощность, рассеиваемая на нагрузке, будет иметь максимальное значение.

Значение максимальной передачи мощности

Замените $ R_L = R_ {Th} \: \ & \: P_L = P_ {L, Max} $ в уравнении 1.

$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th}) ^ 2} \ rbrace $$

$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace $$

$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$

$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}, \: с тех пор как \: R_ {L} = R_ {Th} $$

Следовательно, максимальная мощность, передаваемая нагрузке, составляет

$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} $$

Эффективность передачи максимальной мощности

Мы можем рассчитать эффективность передачи максимальной мощности, $ \ eta_ {Max} $, используя следующую формулу.

$ \ eta_ {Max} = \ frac {P_ {L, Max}} {P_S} $ Уравнение 2

Куда,

• $ P_ {L, Max} $ — это максимальное количество энергии, передаваемой нагрузке.

• $ P_S $ — количество энергии, генерируемой источником.

$ P_ {L, Max} $ — это максимальное количество энергии, передаваемой нагрузке.

$ P_S $ — количество энергии, генерируемой источником.

Количество энергии, генерируемой источником

$$ P_S = 2 I ^ 2 R_ {Th} + I ^ 2 R_L $$

$$ \ Rightarrow P_S = 2 I ^ 2 R_ {Th}, \: с \: R_ {L} = R_ {Th} $$

• Замените $ I = \ frac {V_ {Th}} {2 R_ {Th}} $ в приведенном выше уравнении.

Замените $ I = \ frac {V_ {Th}} {2 R_ {Th}} $ в приведенном выше уравнении.

$$ P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th} $$

$$ \ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th} $$

$$ \ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th}} $$

• Подставьте значения $ P_ {L, Max} $ и $ P_S $ в уравнение 2.

Подставьте значения $ P_ {L, Max} $ и $ P_S $ в уравнение 2.

$$ \ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} { 2R_ {Th}} \ rgroup} $$

$$ \ Rightarrow \ eta_ {Max} = \ frac {1} {2} $$

Мы можем представить эффективность передачи максимальной мощности в процентах следующим образом:

$$ \% \ eta_ {Max} = \ eta_ {Max} \ times 100 \% $$

$$ \ Rightarrow \% \ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ times 100 \% $$

$$ \ Rightarrow \% \ eta_ {Max} = 50 \% $$

Следовательно, эффективность передачи максимальной мощности составляет 50% .

пример

Найдите максимальную мощность, которая может быть подана на нагрузочный резистор R _L цепи, показанной на следующем рисунке.

Шаг 1 — В главе «Теорема Тевенина» мы вычислили эквивалентную схему Тевенина с левой стороны клемм A и B. Теперь мы можем использовать эту схему. Это показано на следующем рисунке.

Здесь напряжение Тевенина $ V_ {Th} = \ frac {200} {3} V $ и сопротивление Тевенина $ R_ {Th} = \ frac {40} {3} \ Omega $

Шаг 2 — Замените часть цепи, которая находится с левой стороны от клемм A и B данной цепи, с вышеуказанной эквивалентной схемой Thevenin. Результирующая принципиальная схема показана на следующем рисунке.

Шаг 3 — Мы можем найти максимальную мощность, которая будет подана на нагрузочный резистор, R _L , используя следующую формулу.

$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$

Замените $ V_ {Th} = \ frac {200} {3} V $ и $ R_ {Th} = \ frac {40} {3} \ Omega $ в приведенной выше формуле.

$$ P_ {L, Max} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup} $$

$$ P_ {L, Max} = \ frac {250} {3} W $$

Следовательно, максимальная мощность, которая будет подаваться на нагрузочный резистор RL данной цепи, составляет $ \ mathbf {\ frac {250} {3}} $ W

Теория сети — отклик цепей постоянного тока

Если выход электрической цепи для входа изменяется во времени, то это называется временной реакцией . Время отклика состоит из следующих двух частей.

• Переходный ответ
• Устойчивый государственный ответ

В этой главе сначала давайте обсудим эти два отклика, а затем рассмотрим эти два отклика в последовательной цепи RL, когда она возбуждается источником постоянного напряжения.

Переходный ответ

После применения входа к электрической цепи, выходу требуется определенное время для достижения устойчивого состояния. Таким образом, выходной сигнал будет в переходном состоянии, пока он не перейдет в устойчивое состояние. Следовательно, отклик электрической цепи во время переходного состояния известен как переходный отклик .

Переходный отклик будет нулевым для больших значений «t». В идеале это значение t должно быть бесконечностью. Но практически пяти постоянных времени достаточно.

Присутствие или отсутствие переходных процессов

Переходные процессы происходят в ответе из-за внезапного изменения в источниках, которые применяются к электрической цепи и / или из-за действия переключения. Есть два возможных переключения. Это выключатель размыкания и замыкания.

• Переходная часть не будет присутствовать в ответе электрической цепи или сети, если она содержит только сопротивления. Потому что резистор имеет возможность регулировать любое количество напряжения и тока.

• Переходная часть возникает в ответе электрической цепи или сети из-за присутствия элементов накопления энергии, таких как индуктор и конденсатор . Потому что они не могут мгновенно изменить энергию, хранящуюся в этих элементах.

Переходная часть не будет присутствовать в ответе электрической цепи или сети, если она содержит только сопротивления. Потому что резистор имеет возможность регулировать любое количество напряжения и тока.

Переходная часть возникает в ответе электрической цепи или сети из-за присутствия элементов накопления энергии, таких как индуктор и конденсатор . Потому что они не могут мгновенно изменить энергию, хранящуюся в этих элементах.

Поведение индуктора

Предположим, что действие переключения происходит при t = 0. Ток индуктора не изменяется мгновенно, когда происходит действие переключения. Это означает, что значение тока индуктора сразу после действия переключения будет таким же, как и перед действием переключения.

Математически это можно представить как

$$ i_L (0 ^ +) = i_L (0 ^ -) $$

Конденсаторное поведение

Напряжение на конденсаторе не изменяется мгновенно, подобно току индуктора, когда происходит переключающее действие. Это означает, что значение напряжения на конденсаторе сразу после переключения будет таким же, как и перед переключением.

Математически это можно представить как

$$ v_c (0 ^ +) = v_c (0 ^ -) $$

Устойчивый государственный ответ

Часть временного отклика, которая остается даже после того, как переходный отклик стал нулевым значением для больших значений «t», называется устойчивым откликом . Это означает, что не будет никакой переходной части в ответе в устойчивом состоянии.

Поведение индуктора

Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько катушек индуктивности и резисторов (дополнительно) в течение длительного времени, то эта электрическая цепь или сеть, как говорят, находятся в устойчивом состоянии. Следовательно, энергия, запасенная в катушке индуктивности этой электрической цепи, максимальна и постоянна.

Математически это можно представить как

$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Максимум и константа

$ \ Rightarrow i_L = $ Максимум и константа

Следовательно, индуктор действует как источник постоянного тока в устойчивом состоянии.

Напряжение на индуктивности будет

$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$

Таким образом, индуктор действует как короткое замыкание в устойчивом состоянии.

Конденсаторное поведение

Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько конденсаторов и резисторов (необязательно), в течение длительного времени, то говорят, что эта электрическая цепь или сеть находятся в устойчивом состоянии. Следовательно, энергия, запасенная в конденсаторе (-ах) этой электрической цепи, является максимальной и постоянной.

Математически это можно представить как

$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Максимум и константа

$ \ Rightarrow v_c = $ Максимум и константа

Следовательно, конденсатор действует как источник постоянного напряжения в устойчивом состоянии.

Ток, протекающий через конденсатор, будет

$$ i_c = C \ frac {dv_c} {dt} = 0A $$

Таким образом, конденсатор действует как разомкнутая цепь в устойчивом состоянии.

Нахождение ответа серии RL Circuit

Рассмотрим следующую схему RL серии .

В вышеупомянутой схеме переключатель оставался открытым до t = 0, и он был закрыт при t = 0. Таким образом, источник постоянного напряжения, имеющий V вольт, не подключен к последовательной цепи RL до этого момента. Следовательно, через индуктор не протекает начальный ток .

Принципиальная электрическая схема, когда переключатель находится в закрытом положении, показана на следующем рисунке.

Теперь ток i течет во всей схеме, поскольку источник постоянного напряжения, имеющий V вольт, подключен к последовательной цепи RL.

Теперь примените KVL вокруг петли.

$$ V = Ri + L \ frac {di} {dt} $$

$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $ Уравнение 1

Вышеупомянутое уравнение является дифференциальным уравнением первого порядка, и оно имеет вид

$ \ frac {dy} {dt} + Py = Q $ Уравнение 2

Сравнивая Уравнение 1 и Уравнение 2, мы получим следующие соотношения.

$$ x = t $$

$$ y = i $$

$$ P = \ frac {R} {L} $$

$$ Q = \ frac {V} {L} $$

Решение уравнения 2 будет

$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $ Уравнение 3

Где k постоянная

Подставим значения x, y, P & Q в уравнение 3.

$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $

$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + к $

$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $

$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $ Уравнение 4

Мы знаем, что в цепи нет начального тока. Следовательно, замените t = 0 и ? = 0 в уравнении 4, чтобы найти значение константы k .

$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$

$$ 0 = \ frac {V} {R} + k (1) $$

$$ k = — \ frac {V} {R} $$

Подставим значение k в уравнение 4.

$$ i = \ frac {V} {R} + \ lgroup — \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

$$ i = \ frac {V} {R} — \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

Следовательно, ток, протекающий по цепи

$ i = — \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $ Уравнение 5

Итак, отклик цепи последовательного RL, когда она возбуждается источником постоянного напряжения, имеет следующие два члена.

• Первый член $ — \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ соответствует переходному ответу .

• Второе слагаемое $ \ frac {V} {R} $ соответствует отклику установившегося состояния . Эти два ответа показаны на следующем рисунке.

Первый член $ — \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ соответствует переходному ответу .

Второе слагаемое $ \ frac {V} {R} $ соответствует отклику установившегося состояния . Эти два ответа показаны на следующем рисунке.

Мы можем переписать уравнение 5 следующим образом:

$ i = \ frac {V} {R} \ lgroup 1 — e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $

$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 — e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $ Уравнение 6

Где τ — постоянная времени, и ее значение равно $ \ frac {L} {R} $.

И Уравнение 5, и Уравнение 6 одинаковы. Но мы можем легко понять вышеуказанную форму волны тока, протекающего по цепи из уравнения 6, подставив несколько значений t, таких как 0, τ, 2τ, 5τ и т. Д.

В приведенной выше форме волны тока, протекающего по цепи, переходный отклик будет представлять до пяти постоянных времени от нуля, тогда как отклик в установившемся режиме будет присутствовать с пяти постоянных времени.

Теория сети — отклик цепей переменного тока

В предыдущей главе мы обсудили переходную характеристику и реакцию установившегося состояния цепи постоянного тока. В этой главе давайте обсудим реакцию цепи переменного тока . Понятия как переходного отклика, так и отклика в стационарном состоянии, которые мы обсуждали в предыдущей главе, также будут здесь полезны.

Нахождение ответа серии RL Circuit

Рассмотрим следующую схему RL серии .

В вышеупомянутой схеме переключатель оставался открытым до t = 0, и он был закрыт при t = 0 . Таким образом, источник переменного напряжения, имеющий пиковое напряжение V _m вольт, не подключен к последовательной цепи RL до этого момента. Следовательно, через индуктор не протекает начальный ток .

Принципиальная схема, когда переключатель находится в закрытом положении, показана на следующем рисунке.

Теперь ток i (t) течет во всей схеме, поскольку источник переменного напряжения, имеющий пиковое напряжение V _m вольт, подключен к последовательной цепи RL.

Мы знаем, что ток i (t), протекающий через вышеуказанную схему, будет иметь два члена, один из которых представляет переходную часть, а другой — стационарное состояние.

Математически это можно представить как

$ i (t) = i_ {Tr} (t) + i_ {ss} (t) $ Уравнение 1

Куда,

• $ i_ {Tr} (t) $ — переходная характеристика тока, протекающего по цепи.

• $ i_ {ss} (t) $ — это установившаяся реакция тока, протекающего по цепи.

$ i_ {Tr} (t) $ — переходная характеристика тока, протекающего по цепи.

$ i_ {ss} (t) $ — это установившаяся реакция тока, протекающего по цепи.

В предыдущей главе мы получили переходный отклик тока, протекающего через последовательную цепь RL. Он имеет вид $ Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $.

Замените $ i_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ в уравнении 1.

$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss} (t) $ Уравнение 2

Расчет установившегося состояния тока

Если синусоидальный сигнал подается в качестве входа в линейную электрическую цепь, то он генерирует устойчивый выходной сигнал, который также является синусоидальным сигналом . И входной, и выходной синусоидальные сигналы будут иметь одинаковую частоту, но разные амплитуды и фазовые углы.

Мы можем рассчитать реакцию стационарного состояния электрической цепи, когда она возбуждается синусоидальным источником напряжения, используя метод преобразования Лапласа .

Схема s-домена, когда переключатель находится в закрытом положении, показана на следующем рисунке.

В приведенной выше схеме все величины и параметры представлены в s-области . Это преобразования Лапласа величин и параметров во временной области.

Передаточная функция вышеуказанной цепи

$$ H (s) = \ frac {I (s)} {V (s)} $$

$$ \ Rightarrow H (s) = \ frac {1} {Z (s)} $$

$$ \ Rightarrow H (s) = \ frac {1} {R + sL} $$

Замените $ s = j \ omega $ в приведенном выше уравнении.

$$ H (j \ omega) = \ frac {1} {R + j \ omega L} $$

Величина $ \ mathbf {\ mathit {H (j \ omega)}} $ равна

$$ | H (j \ omega) | = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$

Фазовый угол $ \ mathbf {\ mathit {H (j \ omega)}} $ равен

$$ \ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$

Мы получим ток установившегося состояния $ i_ {ss} (t) $, выполнив следующие два шага:

• Умножьте пиковое напряжение входного синусоидального напряжения на величину $ H (j \ omega) $.

• Добавьте фазовые углы входного синусоидального напряжения и $ H (j \ omega) $.

Умножьте пиковое напряжение входного синусоидального напряжения на величину $ H (j \ omega) $.

Добавьте фазовые углы входного синусоидального напряжения и $ H (j \ omega) $.

Ток установившегося состояния $ i_ {ss} (t) $ будет

$$ i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

Подставьте значение $ i_ {ss} (t) $ в уравнение 2.

$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $ Уравнение 3

Мы знаем, что в цепи нет начального тока. Следовательно, замените t = 0 & i (t) = 0 в уравнении 3, чтобы найти значение постоянной, K.

$$ 0 = Ke ^ {- \ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega (0) + \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

$$ \ Rightarrow K = — \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

Подставьте значение K в уравнение 3.

$ i (t) = — \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $ Уравнение 4

Уравнение 4 представляет ток, протекающий через последовательную цепь RL, когда он возбуждается синусоидальным источником напряжения. У него два срока. Первое и второе слагаемые представляют переходный отклик и отклик устойчивого состояния тока соответственно.

Мы можем пренебречь первым слагаемым в уравнении 4, потому что его значение будет намного меньше единицы. Таким образом, результирующий ток, протекающий через цепь будет

$$ i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi — tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

Он содержит только термин устойчивого состояния . Следовательно, мы можем найти только отклик устойчивого состояния цепей переменного тока и пренебречь переходным откликом от него.

Теория сети — серия резонанс

Резонанс возникает в электрических цепях из-за наличия элементов накопления энергии, таких как индуктор и конденсатор. Это фундаментальная концепция, основанная на том, что радиоприемники и телевизионные приемники спроектированы таким образом, чтобы они могли выбирать только желаемую частоту станции.

Существует два типа резонансов, а именно последовательный резонанс и параллельный резонанс. Они классифицируются на основе сетевых элементов, которые соединены последовательно или параллельно. В этой главе давайте поговорим о последовательном резонансе.

Схема последовательного резонанса

Если резонанс возникает в последовательной цепи RLC, то он называется последовательным резонансом . Рассмотрим следующую серию RLC-схемы , которая представлена ​​в векторной области.

Здесь пассивные элементы, такие как резистор, катушка индуктивности и конденсатор, соединены последовательно. Вся эта комбинация последовательно соединена с источником синусоидального напряжения.

Примените КВЛ вокруг петли.

$$ V — V_R — V_L — V_C = 0 $$

$$ \ Rightarrow V — IR — I (j X_L) — I (-j X_C) = 0 $$

$$ \ Rightarrow V = IR + I (j X_L) + I (-j X_C) $$

$ \ Rightarrow V = I [R + j (X_L — X_C)] $ Уравнение 1

Приведенное выше уравнение имеет вид V = IZ .

Следовательно, полное сопротивление Z последовательной цепи RLC будет

$$ Z = R + j (X_L — X_C) $$

Параметры и электрические величины при резонансе

Теперь давайте по порядку выведем значения параметров и электрических величин при резонансе последовательной цепи RLC.

Резонансная частота

Частота, на которой возникает резонанс, называется резонансной частотой f _r . В последовательной цепи RLC резонанс возникает, когда мнимый член импеданса Z равен нулю, т. Е. Значение $ X_L — X_C $ должно быть равно нулю.

$$ \ Rightarrow X_L = X_C $$

Замените $ X_L = 2 \ pi f L $ и $ X_C = \ frac {1} {2 \ pi f C} $ в вышеприведенном уравнении.

$$ 2 \ pi f L = \ frac {1} {2 \ pi f C} $$

$$ \ Rightarrow f ^ 2 = \ frac {1} {(2 \ pi) ^ 2 LC} $$

$$ \ Rightarrow f = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$

Следовательно, резонансная частота f _r последовательной цепи RLC равна

$$ f_r = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$

Где L — индуктивность индуктивности, а C — емкость конденсатора.

Резонансная частота f _r последовательной цепи RLC зависит только от индуктивности L и емкости C. Но это не зависит от сопротивления R.

полное сопротивление

Мы получили сопротивление Z цепи RLC серии как

$$ Z = R + j (X_L — X_C) $$

Замените $ X_L = X_C $ в приведенном выше уравнении.

$$ Z = R + j (X_C — X_C) $$

$$ \ Rightarrow Z = R + j (0) $$

$$ \ Rightarrow Z = R $$

При резонансе импеданс Z последовательной RLC цепи равен значению сопротивления R , т. Е. Z = R.

Ток, протекающий по цепи

Замените $ X_L — X_C = 0 $ в уравнении 1.

$$ V = I [R + j (0)] $$

$$ \ Rightarrow V = IR $$

$$ \ Rightarrow I = \ frac {V} {R} $$

Следовательно, ток, протекающий через последовательную RLC-цепь в резонансе, равен $ \ mathbf {\ mathit {I = \ frac {V} {R}}} $.

В резонансе полное сопротивление последовательной цепи RLC достигает минимального значения. Следовательно, максимальный ток протекает через эту цепь при резонансе.

Напряжение на резисторе

Напряжение на резисторе

$$ V_R = IR $$

Подставьте значение I в приведенное выше уравнение.

$$ V_R = \ lgroup \ frac {V} {R} \ rgroup R $$

$$ \ Rightarrow V_R = V $$

Следовательно, напряжение на резисторе в резонансе составляет V _R = V.

Напряжение на Индукторе

Напряжение на индуктивности

$$ V_L = I (jX_L) $$

Подставьте значение I в приведенное выше уравнение.

$$ V_L = \ lgroup \ frac {V} {R} \ rgroup (jX_L) $$

$$ \ Rightarrow V_L = j \ lgroup \ frac {X_L} {R} \ rgroup V $$

$$ \ Rightarrow V_L = j QV $$

Следовательно, напряжение на катушке индуктивности при резонансе составляет $ V_L = j QV $.

Таким образом, величина напряжения на индуктивности в резонансе будет

$$ | V_L | = QV $$

Где Q — фактор качества, а его значение равно $ \ frac {X_L} {R} $

Напряжение на конденсаторе

Напряжение на конденсаторе

$$ V_C = I (-j X_C) $$

Подставьте значение I в приведенное выше уравнение.

$$ V_C = \ lgroup \ frac {V} {R} \ rgroup (-j X_C) $$

$$ \ Rightarrow V_C = -j \ lgroup \ frac {X_C} {R} \ rgroup V $$

$$ \ Rightarrow V_C = -jQV $$

Таким образом, напряжение на конденсаторе в резонансе составляет $ \ mathbf {\ mathit {V_C = -jQV}} $.

Таким образом, величина напряжения на конденсаторе в резонансе будет

$$ | V_C | = QV $$

Где Q — фактор качества, а его значение равно $ \ frac {X_ {C}} {R} $

Примечание. Последовательная резонансная схема RLC называется схемой увеличения напряжения , поскольку величина напряжения на индуктивности и конденсаторе равна Q, умноженной на входное синусоидальное напряжение V.

Теория сети — параллельный резонанс

В предыдущей главе мы обсуждали важность последовательного резонанса. Теперь давайте обсудим параллельный резонанс в цепях RLC.

Схема параллельного резонанса

Если резонанс возникает в параллельной цепи RLC, то он называется параллельным резонансом . Рассмотрим следующую параллельную схему RLC , которая представлена ​​в векторной области.

Здесь пассивные элементы, такие как резистор, катушка индуктивности и конденсатор, соединены параллельно. Вся эта комбинация параллельна входному синусоидальному источнику тока.

Написать узловое уравнение в узле P.

$$ — I + I_R + I_L + I_C = 0 $$

$$ \ Rightarrow — I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$

$$ \ Rightarrow I = \ frac {V} {R} — \ frac {jV} {X_L} + \ frac {jV} {X_C} $$

$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} — \ frac {1} {X_L} \ rgroup] $ Уравнение 1

Приведенное выше уравнение имеет вид I = VY .

Следовательно, допуск Y параллельной цепи RLC будет

$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} — \ frac {1} {X_L} \ rgroup $$

Параметры и электрические величины при резонансе

Теперь давайте по порядку выведем значения параметров и электрических величин при резонансе параллельной цепи RLC.

Резонансная частота

Мы знаем, что резонансная частота f _r — это частота, на которой возникает резонанс. В параллельной RLC цепи резонанс возникает, когда мнимый член допуска Y равен нулю. т.е. значение $ \ frac {1} {X_C} — \ frac {1} {X_L} $ должно быть равно нулю

$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$

$$ \ Rightarrow X_L = X_C $$

Вышеуказанное условие резонанса такое же, как и в последовательной цепи RLC. Таким образом, резонансная частота f _r будет одинаковой как в последовательной RLC-цепи, так и в параллельной RLC-схеме.

Следовательно, резонансная частота f _r параллельной RLC-схемы равна

$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$

Куда,

• L — индуктивность индуктора.
• С — емкость конденсатора.

Резонансная частота f _r параллельной цепи RLC зависит только от индуктивности L и емкости C. Но это не зависит от сопротивления R.

впуск

Мы получили допуск Y параллельной цепи RLC как

$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} — \ frac {1} {X_L} \ rgroup $$

Замените $ X_L = X_C $ в приведенном выше уравнении.

$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} — \ frac {1} {X_C} \ rgroup $$

$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$

$$ \ Rightarrow Y = \ frac {1} {R} $$

При резонансе вход Y параллельной цепи RLC равен обратной величине сопротивления R. т.е. $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $

Напряжение на каждом элементе

Замените $ \ frac {1} {X_C} — \ frac {1} {X_L} = 0 $ в уравнении 1

$$ I = V [\ frac {1} {R} + j (0)] $$

$$ \ Rightarrow I = \ frac {V} {R} $$

$$ \ Rightarrow V = IR $$

Следовательно, напряжение на всех элементах параллельной цепи RLC при резонансе равно V = IR .

При резонансе допуск параллельной цепи RLC достигает минимального значения. Следовательно, максимальное напряжение присутствует на каждом элементе этой цепи в резонансе.

Ток, протекающий через резистор

Ток, протекающий через резистор

$$ I_R = \ frac {V} {R} $$

Подставим значение V в приведенное выше уравнение.

$$ I_R = \ frac {IR} {R} $$

$$ \ Rightarrow I_R = I $$

Следовательно, ток, протекающий через резистор в резонансе, составляет $ \ mathbf {\ mathit {I_R = I}} $.

Ток, протекающий через индуктор

Ток, протекающий через индуктор

$$ I_L = \ frac {V} {j X_L} $$

Подставим значение V в приведенное выше уравнение.

$$ I_L = \ frac {IR} {j X_L} $$

$$ \ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$

$$ \ Rightarrow I_L = -jQI $$

Следовательно, ток, протекающий через индуктор в резонансе, равен $ I_L = -jQI $.

Итак, величина тока, протекающего через индуктор в резонансе, будет

$$ | I_L | = QI $$

Где Q — фактор качества, а его значение равно $ \ frac {R} {X_L} $

Ток, протекающий через конденсатор

Ток, протекающий через конденсатор

$$ I_C = \ frac {V} {- j X_C} $$

Подставим значение V в приведенное выше уравнение.

$$ I_C = \ frac {IR} {- j X_C} $$

$$ \ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I $$

$$ \ Rightarrow I_C = jQI $$

Следовательно, ток, протекающий через конденсатор в резонансе, составляет $ I_C = jQI $.

Таким образом, величина тока, протекающего через конденсатор при резонансе, будет

$$ | I_C | = QI $$

Где Q — фактор качества, а его значение равно $ \ frac {R} {X_C} $

Примечание. Схема RLC с параллельным резонансом называется схемой увеличения тока. Потому что величина тока, протекающего через индуктор и конденсатор, равна Q, умноженному на входной синусоидальный ток I.

Теория сетей — связанные схемы

Электрическая цепь называется связанной цепью , когда существует взаимная индуктивность между катушками (или катушками индуктивности), присутствующими в этой цепи. Катушка — это не что иное, как последовательная комбинация резистора и индуктора. При отсутствии резистора катушка становится индуктором. Иногда термины катушка и индуктор взаимозаменяемы.

В этой главе сначала давайте поговорим о точечном соглашении, а затем обсудим классификацию связи.

Дот Конвенция

Точечная конвенция — это метод, который дает подробную информацию о полярности напряжения на точечной клемме. Эта информация полезна при написании уравнений КВЛ.

• Если ток поступает на пунктирную клемму одной катушки (или индуктора), то он индуцирует напряжение на другой катушке (или катушке индуктивности), которая имеет положительную полярность на точечной клемме.

• Если ток уходит от пунктирной клеммы одной катушки (или индуктора), то он индуцирует напряжение на другой катушке (или катушке индуктивности), которая имеет отрицательную полярность на точечной клемме.

Если ток поступает на пунктирную клемму одной катушки (или индуктора), то он индуцирует напряжение на другой катушке (или катушке индуктивности), которая имеет положительную полярность на точечной клемме.

Если ток уходит от пунктирной клеммы одной катушки (или индуктора), то он индуцирует напряжение на другой катушке (или катушке индуктивности), которая имеет отрицательную полярность на точечной клемме.

Классификация сцепления

Мы можем классифицировать связь по следующим двум категориям.

• Электрическая муфта
• Магнитная муфта

Теперь давайте обсудим каждый тип связи один за другим.

Электрическая муфта

Электрическая связь возникает, когда существует физическая связь между двумя катушками (или катушками индуктивности). Это соединение может быть вспомогательного или противоположного типа. Это основано на том, входит ли ток в пунктирный терминал или выходит из пунктирного терминала.

Муфта типа Aiding

Рассмотрим следующую электрическую цепь, имеющую два индуктора, соединенных последовательно .

Поскольку два индуктора соединены последовательно, один и тот же ток I протекает через оба индуктора с самоиндуктивностью L ₁ и L ₂ .

В этом случае ток я ввожу на точечный зажим каждого индуктора. Следовательно, индуцированное напряжение в каждом индукторе будет иметь положительную полярность на точечной клемме из-за тока, протекающего в другой катушке.

Примените KVL вокруг петли вышеупомянутой электрической цепи или сети.

$$ V — L_1 \ frac {dI} {dt} — M \ frac {dI} {dt} — L_2 \ frac {dI} {dt} — M \ frac {dI} {dt} = 0 $$

$$ V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} + 2M \ frac {dI} {dt} $$

$$ V = (L_1 + L_2 + 2M) \ frac {dI} {dt} $$

Вышеупомянутое уравнение имеет вид $ \ mathbf {\ mathit {V = L_ {Eq} \ frac {dI} {dt}}} $

Следовательно, эквивалентная индуктивность последовательной комбинации индукторов, показанных на приведенном выше рисунке, равна

$$ L_ {Eq} = L_1 + L_2 + 2M $$

В этом случае эквивалентная индуктивность была увеличена на 2М. Следовательно, вышеуказанная электрическая схема является примером электрической связи вспомогательного типа.

Муфта противоположного типа

Рассмотрим следующую электрическую цепь, имеющую два индуктора, соединенных последовательно .

В вышеупомянутой схеме ток I поступает на пунктирную клемму индуктора, имеющую индуктивность L ₁ . Следовательно, он индуцирует напряжение в другом индукторе, имеющем индуктивность L ₂ . Таким образом, положительная полярность наведенного напряжения присутствует на точечной клемме этого индуктора.

В приведенной выше схеме ток I выходит из пунктирной клеммы индуктора, имеющего индуктивность L ₂ . Следовательно, он индуцирует напряжение в другом индукторе, имеющем индуктивность L ₁ . Таким образом, отрицательная полярность наведенного напряжения присутствует на точечной клемме этого индуктора.

Примените KVL вокруг петли вышеупомянутой электрической цепи или сети.

$$ V — L_1 \ frac {dI} {dt} + M \ frac {dI} {dt} — L_2 \ frac {dI} {dt} + M \ frac {dI} {dt} = 0 $$

$$ \ Rightarrow V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} — 2M \ frac {dI} {dt} $$

$$ \ Rightarrow V = (L_1 + L_2 — 2M) \ frac {dI} {dt} $$

Вышеупомянутое уравнение имеет вид $ \ mathbf {\ mathit {V = L_ {Eq} \ frac {dI} {dt}}} $

Следовательно, эквивалентная индуктивность последовательной комбинации индукторов, показанных на приведенном выше рисунке, равна

$$ L_ {Eq} = L_1 + L_2 — 2M $$

В этом случае эквивалентная индуктивность была уменьшена на 2М. Следовательно, вышеуказанная электрическая схема является примером электрической связи противоположного типа.

Магнитная муфта

Магнитная связь возникает, когда нет физической связи между двумя катушками (или катушками индуктивности). Это соединение может быть вспомогательного или противоположного типа. Это основано на том, входит ли ток в пунктирный терминал или выходит из пунктирного терминала.

Муфта типа Aiding

Рассмотрим следующую электрическую эквивалентную цепь трансформатора . Он имеет две катушки, и они называются первичными и вторичными катушками.

Токи, протекающие через первичную и вторичную катушки, равны i ₁ и i ₂ соответственно. В этом случае эти токи входят в пунктирную клемму соответствующей катушки. Следовательно, индуцированное напряжение в каждой катушке будет иметь положительную полярность на точечной клемме из-за тока, протекающего в другой катушке.

Примените КВЛ вокруг первичной катушки.

$$ v_1 — L_1 \ frac {d i_1} {dt} — M \ frac {d i_2} {dt} = 0 $$

$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} $ Уравнение 1

Примените КВЛ вокруг вторичной катушки.

$$ v_2 — L_2 \ frac {d i_2} {dt} — M \ frac {d i_1} {dt} = 0 $$

$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} $ Уравнение 2

В уравнении 1 и уравнении 2 самоиндуцированное напряжение и взаимно индуцированное напряжение имеют одинаковую полярность. Следовательно, вышеупомянутая схема трансформатора является примером магнитной связи , которая имеет вспомогательный тип.

Сцепление противоположного типа

Рассмотрим следующую электрическую эквивалентную цепь трансформатора .

Токи, протекающие через первичную и вторичную катушки, равны i ₁ и i ₂ соответственно. В этом случае ток i ₁ поступает на точечный вывод первичной катушки. Следовательно, это вызывает напряжение во вторичной катушке. Таким образом, положительная полярность наведенного напряжения присутствует на точечном выводе этой вторичной катушки.

В приведенной выше схеме ток i ₂ выходит из пунктирной клеммы вторичной катушки. Следовательно, это вызывает напряжение в первичной катушке. Таким образом, отрицательная полярность наведенного напряжения присутствует на точечном выводе этой первичной катушки.

Примените КВЛ вокруг первичной катушки.

$$ v_1 — L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} = 0 $$

$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} — M \ frac {d i_2} {dt} $ Уравнение 3

Примените КВЛ вокруг вторичной катушки.

$$ v_2 — L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} = 0 $$

$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} — M \ frac {d i_1} {dt} $ Уравнение 4

В уравнении 3 и уравнении 4 самоиндуцированное напряжение и взаимно индуцированное напряжение имеют противоположную полярность. Следовательно, приведенная выше схема трансформатора является примером магнитной связи противоположного типа.

Теория сетей — двухпортовые сети

В общем, легко проанализировать любую электрическую сеть, если она представлена ​​эквивалентной моделью, которая дает соотношение между входными и выходными переменными. Для этого мы можем использовать два представления сети порта . Как следует из названия, две сети портов содержат два порта. Среди которых один порт используется в качестве входного порта, а другой порт используется в качестве выходного порта. Первый и второй порты называются port1 и port2 соответственно.

Сеть с одним портом представляет собой двухполюсную электрическую сеть, в которой ток поступает через один терминал и выходит через другой терминал. Резисторы, катушки индуктивности и конденсаторы являются примерами сети с одним портом, потому что каждый из них имеет две клеммы. Представление сети одного порта показано на следующем рисунке.

Здесь пара терминалов 1 и 1 ‘представляет порт. В этом случае у нас есть только один порт, так как это сеть с одним портом.

Аналогично, двухпортовая сеть представляет собой пару двухполюсных электрических сетей, в которых ток поступает через один терминал и выходит через другой терминал каждого порта. Двухпортовое сетевое представление показано на следующем рисунке.

Здесь одна пара терминалов 1 & 1 ‘представляет один порт, который называется port1, а другая пара терминалов 2 & 2′ представляет другой порт, который называется port2 .

В сети с двумя портами есть четыре переменные V ₁ , V ₂ , I ₁ и I _2, как показано на рисунке. Из которых мы можем выбрать две переменные как независимые и еще две переменные как зависимые. Итак, мы получим шесть возможных пар уравнений. Эти уравнения представляют зависимые переменные в терминах независимых переменных. Коэффициенты независимых переменных называются параметрами . Итак, каждая пара уравнений даст набор из четырех параметров.

Параметры двухпортовой сети

Параметры сети с двумя портами называются параметрами сети с двумя портами или просто параметрами двух портов. Ниже приведены типы параметров сети двух портов.

• Z параметры
• Y параметры
• Т параметры
• Т ‘параметры
• ч-параметры
• г-параметры

Теперь давайте поговорим об этих двух параметрах сети портов один за другим.

Z параметры

Мы получим следующий набор из двух уравнений, рассматривая переменные V ₁ и V ₂ как зависимые, а I ₁ и I ₂ как независимые. Коэффициенты независимых переменных I ₁ и I ₂ называются Z параметрами .

$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$

$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$

Z параметры

$$ Z_ {11} = \ frac {V_1} {I_1}, \: когда \: I_2 = 0 $$

$$ Z_ {12} = \ frac {V_1} {I_2}, \: когда \: I_1 = 0 $$

$$ Z_ {21} = \ frac {V_2} {I_1}, \: когда \: I_2 = 0 $$

$$ Z_ {22} = \ frac {V_2} {I_2}, \: когда \: I_1 = 0 $$

Параметры Z называются параметрами импеданса, потому что это просто соотношения напряжений и токов. Единицами Z параметров являются Ом (Ом).

Мы можем рассчитать два параметра Z, Z ₁₁ и Z ₂₁ , выполнив разомкнутую цепь порта 2. Точно так же мы можем вычислить два других параметра Z, Z ₁₂ и Z ₂₂ , выполнив разомкнутую цепь порта 1. Следовательно, параметры Z также называются параметрами полного сопротивления разомкнутой цепи .

Y параметры

Мы получим следующий набор из двух уравнений, рассматривая переменные I ₁ и I ₂ как зависимые и V ₁ и V ₂ как независимые. Коэффициенты независимых переменных V ₁ и V ₂ называются параметрами Y.

$$ I_1 = Y_ {11} V_1 + Y_ {12} V_2 $$

$$ I_2 = Y_ {21} V_1 + Y_ {22} V_2 $$

Y параметры

$$ Y_ {11} = \ frac {I_1} {V_1}, \: когда \: V_2 = 0 $$

$$ Y_ {12} = \ frac {I_1} {V_2}, \: когда \: V_1 = 0 $$

$$ Y_ {21} = \ frac {I_2} {V_1}, \: когда \: V_2 = 0 $$

$$ Y_ {22} = \ frac {I_2} {V_2}, \: когда \: V_1 = 0 $$

Параметры Y называются параметрами допуска, потому что это просто соотношения токов и напряжений. Единицами измерения Y-параметров являются mho.

Мы можем рассчитать два параметра Y, Y ₁₁ и Y ₂₁ , выполнив короткое замыкание порта 2. Точно так же мы можем вычислить два других параметра Y, Y ₁₂ и Y ₂₂ , делая короткое замыкание порта 1. Следовательно, параметры Y также называются параметрами допуска короткого замыкания .

Т параметры

Мы получим следующий набор из двух уравнений, рассматривая переменные V ₁ и I ₁ как зависимые и V ₂ и I ₂ как независимые. Коэффициенты V ₂ и -I ₂ называются T параметрами .

$$ V_1 = A V_2 — B I_2 $$

$$ I_1 = C V_2 — D I_2 $$

Т параметры являются

$$ A = \ frac {V_1} {V_2}, \: когда \: I_2 = 0 $$

$$ B = — \ frac {V_1} {I_2}, \: когда \: V_2 = 0 $$

$$ C = \ frac {I_1} {V_2}, \: когда \: I_2 = 0 $$

$$ D = — \ frac {I_1} {I_2}, \: когда \: V_2 = 0 $$

Параметры T называются параметрами передачи или параметрами ABCD . Параметры A и D не имеют каких-либо единиц измерения, поскольку они меньше по размеру. Единицами измерения параметров B и C являются ом и мхо соответственно.

Мы можем рассчитать два параметра, A и C, выполнив разомкнутую цепь порта2. Точно так же мы можем вычислить два других параметра, B и D, делая короткое замыкание порта 2.

Т ‘параметры

Мы получим следующий набор из двух уравнений, рассматривая переменные V ₂ и I ₂ как зависимые и V ₁ и I ₁ как независимые. Коэффициенты V ₁ и -I ₁ называются параметрами T ‘ .

$$ V_2 = A ‘V_1 — B’ I_1 $$

$$ I_2 = C ‘V_1 — D’ I_1 $$

Т параметры являются

$$ A ‘= \ frac {V_2} {V_1}, \: когда \: I_1 = 0 $$

$$ B ‘= — \ frac {V_2} {I_1}, \: когда \: V_1 = 0 $$

$$ C ‘= \ frac {I_2} {V_1}, \: когда \: I_1 = 0 $$

$$ D ‘= — \ frac {I_2} {I_1}, \: когда \: V_1 = 0 $$

Параметры T ‘называются параметрами обратной передачи или параметрами A’B’C’D’ . Параметры A ‘и D’ не имеют каких-либо единиц измерения, поскольку они меньше по размеру. Единицами параметров B ‘и C’ являются Ом и Мхо соответственно.

Мы можем рассчитать два параметра, A ‘и C’, выполнив разомкнутую цепь порта1. Точно так же мы можем вычислить два других параметра, B ‘и D’, выполнив короткое замыкание порта 1.

ч-параметры

Мы получим следующий набор из двух уравнений, рассматривая переменные V ₁ и I ₂ как зависимые, а I ₁ и V ₂ как независимые. Коэффициенты независимых переменных, I ₁ и V ₂ , называются h-параметрами .

$$ V_1 = h_ {11} I_1 + h_ {12} V_2 $$

$$ I_2 = h_ {21} I_1 + h_ {22} V_2 $$

H-параметры

$$ h_ {11} = \ frac {V_1} {I_1}, \: когда \: V_2 = 0 $$

$$ h_ {12} = \ frac {V_1} {V_2}, \: когда \: I_1 = 0 $$

$$ h_ {21} = \ frac {I_2} {I_1}, \: когда \: V_2 = 0 $$

$$ h_ {22} = \ frac {I_2} {V_2}, \: когда \: I_1 = 0 $$

h-параметры называются гибридными параметрами . Параметры h ₁₂ и h ₂₁ не имеют каких-либо единиц измерения, поскольку они не имеют размеров. Единицами параметров h ₁₁ и h ₂₂ являются Ом и Мхо соответственно.

Мы можем вычислить два параметра, h ₁₁ и h ₂₁ , делая короткое замыкание порта 2. Точно так же мы можем вычислить два других параметра, h ₁₂ и h ₂₂ , выполнив разомкнутую цепь порта 1.

H-параметры или гибридные параметры полезны в схемах (сетях) моделирования транзисторов.

г-параметры

Мы получим следующий набор из двух уравнений, рассматривая переменные I ₁ и V ₂ как зависимые и V ₁ и I ₂ как независимые. Коэффициенты независимых переменных V ₁ и I ₂ называются g-параметрами .

$$ I_1 = g_ {11} V_1 + g_ {12} I_2 $$

$$ V_2 = g_ {21} V_1 + g_ {22} I_2 $$

G-параметры

$$ g_ {11} = \ frac {I_1} {V_1}, \: когда \: I_2 = 0 $$

$$ g_ {12} = \ frac {I_1} {I_2}, \: когда \: V_1 = 0 $$

$$ g_ {21} = \ frac {V_2} {V_1}, \: когда \: I_2 = 0 $$

$$ g_ {22} = \ frac {V_2} {I_2}, \: когда \: V_1 = 0 $$

g-параметры называются обратными гибридными параметрами . Параметры g ₁₂ и g ₂₁ не имеют каких-либо единиц измерения, поскольку они меньше по размеру. Единицами параметров g ₁₁ и g ₂₂ являются mho и ом соответственно.

Мы можем рассчитать два параметра, g ₁₁ и g ₂₁ , выполнив разомкнутую цепь порта 2. Точно так же мы можем вычислить два других параметра, g ₁₂ и g ₂₂ , делая короткое замыкание порта 1.

Двухпортовые преобразования параметров

В предыдущей главе мы обсудили шесть типов параметров двухпортовой сети. Теперь давайте преобразуем один набор параметров сети с двумя портами в другой набор параметров сети с двумя портами. Это преобразование известно как преобразование параметров сети с двумя портами или просто преобразование параметров с двумя портами .

Иногда легко легко найти один набор параметров данной электрической сети. В этих ситуациях мы можем преобразовать эти параметры в требуемый набор параметров вместо того, чтобы вычислять эти параметры напрямую с большим трудом.

Теперь давайте обсудим некоторые преобразования двух параметров порта.

Процедура преобразования двух параметров порта

Выполните следующие действия, преобразуя один набор двухпортовых сетевых параметров в другой набор двухпортовых сетевых параметров.

• Шаг 1 — Запишите уравнения двухпортовой сети с точки зрения желаемых параметров.

• Шаг 2 — Запишите уравнения двухпортовой сети с точки зрения заданных параметров.

• Шаг 3 — Переставьте уравнения шага 2 таким образом, чтобы они были похожи на уравнения шага 1.

• Шаг 4 — Приравнивая аналогичные уравнения Шаг 1 и Шаг 3, мы получим желаемые параметры в терминах заданных параметров. Мы можем представить эти параметры в виде матрицы.

Шаг 1 — Запишите уравнения двухпортовой сети с точки зрения желаемых параметров.

Шаг 2 — Запишите уравнения двухпортовой сети с точки зрения заданных параметров.

Шаг 3 — Переставьте уравнения шага 2 таким образом, чтобы они были похожи на уравнения шага 1.

Шаг 4 — Приравнивая аналогичные уравнения Шаг 1 и Шаг 3, мы получим желаемые параметры в терминах заданных параметров. Мы можем представить эти параметры в виде матрицы.

Z параметры для Y параметров

Здесь мы должны представить параметры Y в терминах параметров Z. Таким образом, в этом случае параметры Y являются желаемыми параметрами, а параметры Z являются заданными параметрами.

Шаг 1 — Мы знаем, что следующий набор из двух уравнений, который представляет собой двухпортовую сеть с точки зрения параметров Y.

$$ I_1 = Y_ {11} V_1 + Y_ {12} V_2 $$

$$ I_2 = Y_ {21} V_1 + Y_ {22} V_2 $$

Мы можем представить два приведенных выше уравнения в матричной форме в виде

$ \ begin {bmatrix} I_1 \\ I_2 \ end {bmatrix} = \ begin {bmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {bmatrix} \ begin {bmatrix } V_1 \\ V_2 \ end {bmatrix} $ Уравнение 1

Шаг 2 — Мы знаем, что приведен следующий набор из двух уравнений, который представляет собой двухпортовую сеть в терминах Z-параметров .

$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$

$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$

Мы можем представить два приведенных выше уравнения в матричной форме в виде

$$ \ begin {bmatrix} V_1 \\ V_2 \ end {bmatrix} = \ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix} \ begin { bmatrix} I_1 \\ I_2 \ end {bmatrix} $$

Шаг 3 — Мы можем изменить его как

$ \ begin {bmatrix} I_1 \\ I_2 \ end {bmatrix} = \ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix} ^ {- 1 } \ begin {bmatrix} V_1 \\ V_2 \ end {bmatrix} $ Уравнение 2

Шаг 4 — Приравнивая уравнение 1 и уравнение 2, мы получим

$$ \ begin {bmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {bmatrix} = \ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix} ^ {- 1} $$

$$ \ Rightarrow \ begin {bmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {bmatrix} = \ frac {\ begin {bmatrix} Z_ {22} & -Z_ {12} \\ — Z_ {21} & Z_ {11} \ end {bmatrix}} {\ Delta Z} $$

Куда,

$$ \ Delta Z = Z_ {11} Z_ {22} — Z_ {12} Z_ {21} $$

Итак, просто выполнив обратную матрицу Z-параметров , мы получим матрицу Y-параметров.

Z параметров для T параметров

Здесь мы должны представить T параметров через Z параметров. Таким образом, в этом случае параметры T являются желаемыми параметрами, а параметры Z являются заданными параметрами.

Шаг 1 — Мы знаем, что следующий набор из двух уравнений, который представляет двухпортовую сеть в терминах T параметров .

$$ V_1 = A V_2 — B I_2 $$

$$ I_1 = C V_2 — D I_2 $$

Шаг 2 — Мы знаем, что приведен следующий набор из двух уравнений, который представляет собой двухпортовую сеть в терминах Z-параметров .

$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$

$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$

Шаг 3 — Мы можем изменить вышеприведенное уравнение как

$$ \ Rightarrow V_2 — Z_ {22} I_2 = Z_ {21} I_1 $$

$$ \ Rightarrow I_1 = \ lgroup \ frac {1} {Z_ {21}} \ rgroup V_2 — \ lgroup \ frac {Z_ {22}} {Z_ {21}} \ rgroup I_2 $$

Шаг 4. Вышеприведенное уравнение имеет вид $ I_1 = CV_2 — DI_2 $. Вот,

$$ C = \ frac {1} {Z_ {21}} $$

$$ D = \ frac {Z_ {22}} {Z_ {21}} $$

Шаг 5 — Заменить значение $ I_1 $ шага 3 в уравнении $ V_1 $ шага 2.

$$ V_1 = Z_ {11} \ lbrace \ lgroup \ frac {1} {Z_ {12}} \ rgroup V_2 — \ lgroup \ frac {Z_ {22}} {Z_ {21}} \ rgroup I_2 \ rbrace + Z_ {12} I_2 $$

$$ \ Rightarrow V_1 = \ lgroup \ frac {Z_ {11}} {Z_ {21}} \ rgroup V_2 — \ lgroup \ frac {Z_ {11} Z_ {22} — Z_ {12} Z_ {21}} { Z_ {21}} \ rgroup I_2 $$

Шаг 6 — Вышеприведенное уравнение имеет вид $ V_1 = AV_2 — BI_2 $. Вот,

$$ A = \ frac {Z_ {11}} {Z_ {21}} $$

$$ B = \ frac {Z_ {11} Z_ {22} — Z_ {12} Z_ {21}} {Z_ {21}} $$

Шаг 7 — Следовательно, матрица T-параметров

$$ \ begin {bmatrix} A & B \\ C & D \ end {bmatrix} = \ begin {bmatrix} \ frac {Z_ {11}} {Z_ {21}} & \ frac {Z_ {11} Z_ { 22} — Z_ {12} Z_ {21}} {Z_ {21}} \\\ frac {1} {Z_ {21}} & \ frac {Z_ {22}} {Z_ {21}} \ end {bmatrix } $$

Y параметры к Z параметрам

Здесь мы должны представить параметры Z в виде параметров Y. Таким образом, в этом случае параметры Z являются желаемыми параметрами, а параметры Y являются заданными параметрами.

Шаг 1 — Мы знаем, что следующее матричное уравнение двухпортовой сети относительно параметров Z как

$ \ begin {bmatrix} V_1 \\ V_2 \ end {bmatrix} = \ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix} \ begin {bmatrix } I_1 \\ I_2 \ end {bmatrix} $ Уравнение 3

Шаг 2 — Мы знаем, что следующее матричное уравнение двухпортовой сети относительно параметров Y как

$$ \ begin {bmatrix} I_1 \\ I_2 \ end {bmatrix} = \ begin {bmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {bmatrix} \ begin { bmatrix} V_1 \\ V_2 \ end {bmatrix} $$

Шаг 3 — Мы можем изменить его как

$ \ begin {bmatrix} V_1 \\ V_2 \ end {bmatrix} = \ begin {bmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {bmatrix} ^ {- 1 } \ begin {bmatrix} I_1 \\ I_2 \ end {bmatrix} $ Уравнение 4

Шаг 4 — Приравнивая уравнение 3 и уравнение 4, мы получим

$$ \ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix} = \ begin {bmatrix} Y_ {11} & Y_ {12} \\ Y_ {21} & Y_ {22} \ end {bmatrix} ^ {- 1} $$

$$ \ Rightarrow \ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix} = \ frac {\ begin {bmatrix} Y_ {22} & — Y_ {12} \\ — Y_ {21} & Y_ {11} \ end {bmatrix}} {\ Delta Y} $$

Куда,

$$ \ Delta Y = Y_ {11} Y_ {22} — Y_ {12} Y_ {21} $$

Итак, просто выполнив обратную матрицу Y-параметров , мы получим матрицу Z-параметров.

Y параметры для T параметров

Здесь мы должны представить параметры T в терминах параметров Y. Таким образом, в этом случае параметры T являются желаемыми параметрами, а параметры Y — заданными параметрами.

Шаг 1 — Мы знаем, что следующий набор из двух уравнений, который представляет двухпортовую сеть в терминах T параметров .

$$ V_1 = A V_2 — B I_2 $$

$$ I_1 = C V_2 — D I_2 $$

Шаг 2 — Мы знаем, что следующий набор из двух уравнений двухпортовой сети относительно параметров Y.

$$ I_1 = Y_ {11} V_1 + Y_ {12} V_2 $$

$$ I_2 = Y_ {21} V_1 + Y_ {22} V_2 $$

Шаг 3 — Мы можем изменить вышеприведенное уравнение как

$$ \ Rightarrow I_2 — Y_ {22} V_2 = Y_ {21} V_1 $$

$$ \ Rightarrow V_1 = \ lgroup \ frac {- Y_ {22}} {Y_ {21}} \ rgroup V_2 — \ lgroup \ frac {-1} {Y_ {21}} \ rgroup I_2 $$

Шаг 4. Вышеприведенное уравнение имеет вид $ V_1 = AV_2 — BI_2 $. Вот,

$$ A = \ frac {- Y_ {22}} {Y_ {21}} $$

$$ B = \ frac {-1} {Y_ {21}} $$

Шаг 5 — Заменить значение $ V_1 $ шага 3 в уравнении $ I_1 $ шага 2.

$$ I_1 = Y_ {11} \ lbrace \ lgroup \ frac {- Y_ {22}} {Y_ {21}} \ rgroup V_2 — \ lgroup \ frac {-1} {Y_ {21}} \ rgroup I_2 \ rbrace + Y_ {12} V_2 $$

$$ \ Rightarrow I_1 = \ lgroup \ frac {Y_ {12} Y_ {21} — Y_ {11} Y_ {22}} {Y_ {21}} \ rgroup V_2 — \ lgroup \ frac {- Y_ {11}} {Y_ {21}} \ rgroup I_2 $$

Шаг 6 — Приведенное выше уравнение имеет вид $ I_1 = CV_2 — DI_2 $. Вот,

$$ C = \ frac {Y_ {12} Y_ {21} — Y_ {11} Y_ {22}} {Y_ {21}} $$

$$ D = \ frac {- Y_ {11}} {Y_ {21}} $$

Шаг 7 — Следовательно, матрица T-параметров

$$ \ begin {bmatrix} A & B \\ C & D \ end {bmatrix} = \ begin {bmatrix} \ frac {-Y_ {22}} {Y_ {21}} & \ frac {-1} {Y_ {21}} \\\ frac {Y_ {12} Y_ {21} — Y_ {11} Y_ {22}} {Y_ {21}} & \ frac {-Y_ {11}} {Y_ {21}} \ конец {bmatrix} $$

T-параметры к h-параметрам

Здесь мы должны представить h-параметры в терминах T-параметров. Таким образом, в этом случае hparameters являются желаемыми параметрами, а T параметры являются заданными параметрами.

Шаг 1 — Мы знаем, что следующие h-параметры двухпортовой сети.

$$ h_ {11} = \ frac {V_1} {I_1}, \: когда \: V_2 = 0 $$

$$ h_ {12} = \ frac {V_1} {V_2}, \: когда \: I_1 = 0 $$

$$ h_ {21} = \ frac {I_2} {I_1}, \: когда \: V_2 = 0 $$

$$ h_ {22} = \ frac {I_2} {V_2}, \: когда \: I_1 = 0 $$

Шаг 2 — Мы знаем, что следующий набор из двух уравнений двухпортовой сети относительно T параметров .

$ V_1 = A V_2 — B I_2 $ Уравнение 5

$ I_1 = C V_2 — D I_2 $ Уравнение 6

Шаг 3 — Замените $ V_2 = 0 $ в вышеприведенных уравнениях, чтобы найти два h-параметра, $ h_ {11} $ и $ h_ {21} $.

$$ \ Rightarrow V_1 = -B I_2 $$

$$ \ Rightarrow I_1 = -D I_2 $$

Подставьте значения $ V_1 $ и $ I_1 $ в h-параметре $ h_ {11} $.

$$ h_ {11} = \ frac {-B I_2} {- D I_2} $$

$$ \ Rightarrow h_ {11} = \ frac {B} {D} $$

Подставьте значение $ I_1 $ в h-параметр $ h_ {21} $.

$$ h_ {21} = \ frac {I_2} {- D I_2} $$

$$ \ Rightarrow h_ {21} = — \ frac {1} {D} $$

Шаг 4 — Заменить $ I_1 = 0 $ во втором уравнении шага 2, чтобы найти h-параметр $ h_ {22} $.

$$ 0 = C V_2 — D I_2 $$

$$ \ Rightarrow C V_2 = D I_2 $$

$$ \ Rightarrow \ frac {I_2} {V_2} = \ frac {C} {D} $$

$$ \ Rightarrow h_ {22} = \ frac {C} {D} $$

Шаг 5 — Замените $ I_2 = \ lgroup \ frac {C} {D} \ rgroup V_2 $ в первом уравнении шага 2, чтобы найти h-параметр, $ h_ {12} $.

$$ V_1 = A V_2 — B \ lgroup \ frac {C} {D} \ rgroup V_2 $$

$$ \ Rightarrow V_1 = \ lgroup \ frac {AD — BC} {D} \ rgroup V_2 $$

$$ \ Rightarrow \ frac {V_1} {V_2} = \ frac {AD — BC} {D} $$

$$ \ Rightarrow h_ {12} = \ frac {AD — BC} {D} $$

Шаг 6 — Следовательно, матрица h-параметров

$$ \ begin {bmatrix} h_ {11} & h_ {12} \\ h_ {21} & h_ {22} \ end {bmatrix} = \ begin {bmatrix} \ frac {B} {D} & \ frac { AD — BC} {D} \\ — \ frac {1} {D} & \ frac {C} {D} \ end {bmatrix} $$

h-параметры для Z-параметров

Здесь мы должны представить Z-параметры через h-параметры. Таким образом, в этом случае Z параметры являются желаемыми параметрами, а h-параметры являются заданными параметрами.

Шаг 1 — Мы знаем, что следующий набор из двух уравнений двухпортовой сети относительно параметров Z.

$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$

$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$

Шаг 2 — Мы знаем, что следующий набор из двух уравнений двухпортовой сети относительно h-параметров .

$$ V_1 = h_ {11} I_1 + h_ {12} V_2 $$

$$ I_2 = h_ {21} I_1 + h_ {22} V_2 $$

Шаг 3 — Мы можем изменить вышеприведенное уравнение как

$$ \ Rightarrow I_2 — h_ {21} I_1 = h_ {22} V_2 $$

$$ \ Rightarrow V_2 = \ frac {I_2 — h_ {21} I_1} {h_ {22}} $$

$$ \ Rightarrow V_2 = \ lgroup \ frac {-h_ {21}} {h_ {22}} \ rgroup I_1 + \ lgroup \ frac {1} {h_ {22}} \ rgroup I_2 $$

Приведенное выше уравнение имеет вид $ V_2 = Z_ {21} I_1 + Z_ {22} I_2. Здесь $

$$ Z_ {21} = \ frac {-h_ {21}} {h_ {22}} $$

$$ Z_ {22} = \ frac {1} {h_ {22}} $$

Шаг 4 — Заменить значение V ₂ в первом уравнении шага 2.

$$ V_1 = h_ {11} I_1 + h_ {21} \ lbrace \ lgroup \ frac {-h_ {21}} {h_ {22}} \ rgroup I_1 + \ lgroup \ frac {1} {h_ {22}} \ rgroup I_2 \ rbrace $$

$$ \ Rightarrow V_1 = \ lgroup \ frac {h_ {11} h_ {22} — h_ {12} h_ {21}} {h_ {22}} \ rgroup I_1 + \ lgroup \ frac {h_ {12}} { h_ {22}} \ rgroup I_2 $$

Приведенное выше уравнение имеет вид $ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $. Вот,

$$ Z_ {11} = \ frac {h_ {11} h_ {22} — h_ {12} h_ {21}} {h_ {22}} $$

$$ Z_ {12} = \ frac {h_ {12}} {h_ {22}} $$

Шаг 5 — Следовательно, матрица параметров Z

$$ \ begin {bmatrix} Z_ {11} & Z_ {12} \\ Z_ {21} & Z_ {22} \ end {bmatrix} = \ begin {bmatrix} \ frac {h_ {11} h_ {22} — h_ {12} h_ {21}} {h_ {22}} & \ frac {h_ {12}} {h_ {22}} \\\ frac {-h_ {21}} {h_ {22}} & \ frac {1} {h_ {22}} \ end {bmatrix} $$

Таким образом, мы можем преобразовать один набор параметров в другой набор параметров.

Теория сети — Фильтры

Фильтры, как следует из названия, они фильтруют частотные компоненты. Это означает, что они допускают определенные частотные компоненты и / или отклоняют некоторые другие частотные компоненты.

В этой главе давайте поговорим о пассивных фильтрах . Это электрические цепи или сети, имеющие пассивные элементы, такие как резистор, катушка индуктивности и конденсатор.

Типы фильтров

Фильтры в основном подразделяются на четыре типа в зависимости от разрешенной полосы частот и / или полосы отклоняющих частот. Ниже приведены типы фильтров.

• Фильтр низких частот
• Фильтр верхних частот
• Полосовой фильтр
• Band Stop Filter

Фильтр низких частот

Фильтр низких частот, как следует из названия, позволяет (пропускает) только низкочастотные компоненты. Это означает, что он отклоняет (блокирует) все другие высокочастотные компоненты.

Схема s-домена (сеть) фильтра нижних частот показана на следующем рисунке.

Он состоит из двух пассивных элементов резистора и конденсатора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на конденсаторе.

Здесь $ V_i (s) $ и $ V_o (s) $ — преобразования Лапласа входного напряжения, $ v_i (t) $ и выходного напряжения, $ v_o (t) $ соответственно.

Передаточная функция вышеуказанной сети

$$ H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {\ frac {1} {sC}} {R + \ frac {1} {sC}} $$

$$ \ Rightarrow H (s) = \ frac {1} {1 + sCR} $$

Замените $ s = j \ omega $ в приведенном выше уравнении.

$$ H (j \ omega) = \ frac {1} {1 + j \ omega CR} $$

Величина передаточной функции равна

$$ | H (j \ omega) | = \ frac {1} {\ sqrt {(1 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 1.

• При $ \ omega = \ frac {1} {CR} $ величина передаточной функции равна 0,707.

• При ω = ∞ величина передаточной функции равна 0.

При ω = 0 величина передаточной функции равна 1.

При $ \ omega = \ frac {1} {CR} $ величина передаточной функции равна 0,707.

При ω = ∞ величина передаточной функции равна 0.

Следовательно, величина передаточной функции фильтра нижних частот будет варьироваться от 1 до 0, так как ω изменяется от 0 до ∞.

Фильтр верхних частот

Фильтр верхних частот, как следует из названия, разрешает (пропускает) только высокочастотные компоненты. Это означает, что он отклоняет (блокирует) все низкочастотные компоненты.

Принципиальная схема s-домена (сеть) фильтра верхних частот показана на следующем рисунке.

Он состоит из двух пассивных элементов — конденсатора и резистора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на резисторе.

Здесь $ V_i (s) $ и $ V_o (s) $ — преобразования Лапласа входного напряжения, $ v_i (t) $ и выходного напряжения, $ v_o (t) $ соответственно.

Передаточная функция вышеуказанной сети

$$ H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {R} {R + \ frac {1} {sC}} $$

$$ \ Rightarrow H (s) = \ frac {sCR} {1 + sCR} $$

Замените $ s = j \ omega $ в приведенном выше уравнении.

$$ H (j \ omega) = \ frac {j \ omega CR} {1 + j \ omega CR} $$

Величина передаточной функции равна

$$ | H (j \ omega) | = \ frac {\ omega CR} {\ sqrt {(1 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 0.

• При $ \ omega = \ frac {1} {CR} $ величина передаточной функции равна 0,707.

• При ω = ∞ величина передаточной функции равна 1.

При ω = 0 величина передаточной функции равна 0.

При $ \ omega = \ frac {1} {CR} $ величина передаточной функции равна 0,707.

При ω = ∞ величина передаточной функции равна 1.

Следовательно, величина передаточной функции фильтра верхних частот будет варьироваться от 0 до 1, так как ω изменяется от 0 до ∞.

Полосовой фильтр

Полосовой фильтр, как следует из названия, позволяет (пропускает) только одну полосу частот. В общем, эта полоса частот находится между низкочастотным диапазоном и высокочастотным диапазоном. Это означает, что этот фильтр отклоняет (блокирует) как низкочастотные, так и высокочастотные компоненты.

Принципиальная схема s-домена (сеть) полосового фильтра показана на следующем рисунке.

Он состоит из трех пассивных элементов индуктора, конденсатора и резистора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на резисторе.

Здесь $ V_i (s) $ и $ V_o (s) $ — преобразования Лапласа входного напряжения, $ v_i (t) $ и выходного напряжения, $ v_o (t) $ соответственно.

Передаточная функция вышеуказанной сети

$$ H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {R} {R + \ frac {1} {sC} + sL} $$

$$ \ Rightarrow H (s) = \ frac {s CR} {s ^ 2 LC + sCR + 1} $$

Замените $ s = j \ omega $ в приведенном выше уравнении.

$$ H (j \ omega) = \ frac {j \ omega CR} {1 — \ omega ^ 2 LC + j \ omega CR} $$

Величина передаточной функции равна

$$ | H (j \ omega) | = \ frac {\ omega CR} {\ sqrt {(1 — \ omega ^ 2 LC) ^ 2 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 0.

• При $ \ omega = \ frac {1} {\ sqrt {LC}} $ величина передаточной функции равна 1.

• При ω = ∞ величина передаточной функции равна 0.

При ω = 0 величина передаточной функции равна 0.

При $ \ omega = \ frac {1} {\ sqrt {LC}} $ величина передаточной функции равна 1.

При ω = ∞ величина передаточной функции равна 0.

Следовательно, величина передаточной функции полосового фильтра будет варьироваться от 0 до 1 и от 1 до 0, так как ω изменяется от 0 до ∞.

Band Stop Filter

Фильтр остановки полосы, как следует из названия, отклоняет (блокирует) только одну полосу частот. В общем, эта полоса частот находится между низкочастотным диапазоном и высокочастотным диапазоном. Это означает, что этот фильтр позволяет (пропускает) как низкочастотные, так и высокочастотные компоненты.

S-домен (сеть) принципиальной схемы и стоп-фильтра показан на следующем рисунке.

Он состоит из трех пассивных элементов: резистора, индуктора и конденсатора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на комбинации индуктивности и конденсатора.

Здесь $ V_i (s) $ и $ V_o (s) $ — преобразования Лапласа входного напряжения, $ v_i (t) $ и выходного напряжения, $ v_o (t) $ соответственно.

Передаточная функция вышеуказанной сети

$$ H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {sL + \ frac {1} {sC}} {R + sL + \ frac {1} {sC}} $$

$$ \ Rightarrow H (s) = \ frac {s ^ 2 LC + 1} {s ^ 2 LC + sCR + 1} $$

Замените $ s = j \ omega $ в приведенном выше уравнении.

$$ H (j \ omega) = \ frac {1 — \ omega ^ 2 LC} {1 — \ omega ^ 2 LC + j \ omega CR} $$

Величина передаточной функции равна

$$ | H (j \ omega) | = \ frac {1 — \ omega ^ 2 LC} {\ sqrt {(1 — \ omega ^ 2 LC) ^ 2 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 1.

• При $ \ omega = \ frac {1} {\ sqrt {LC}} $ величина передаточной функции равна 0.

• При ω = ∞ величина передаточной функции равна 1.

При ω = 0 величина передаточной функции равна 1.

При $ \ omega = \ frac {1} {\ sqrt {LC}} $ величина передаточной функции равна 0.

При ω = ∞ величина передаточной функции равна 1.

Следовательно, величина передаточной функции полосового фильтра будет изменяться от 1 до 0 и от 0 до 1, так как ω изменяется от 0 до ∞.