Матрицы топологии сети

В предыдущей главе мы обсуждали, как преобразовать электрическую цепь в эквивалентный граф. Теперь давайте обсудим Матрицы топологии сети, которые полезны для решения любой проблемы электрической цепи или сети с использованием их эквивалентных графов.

Матрицы, связанные с сетевыми графами

Ниже приведены три матрицы, которые используются в теории графов.

• Матрица заболеваемости
• Матрица фундаментальной петли
• Фундаментальный крой Set Matrix

Матрица заболеваемости

Матрица инцидентности представляет график данной электрической цепи или сети. Следовательно, можно нарисовать график той же электрической цепи или сети из матрицы инцидентности .

Мы знаем, что граф состоит из множества узлов, которые связаны между собой несколькими ветвями. Итак, соединение ветвей с узлом называется инцидентностью. Матрица инцидентности представлена ​​буквой А. Она также называется матрицей инцидентности между узлами или матрицей узлов .

Если в ориентированном графе имеется «n» узлов и «b» ответвлений, то матрица инцидентности будет иметь «n» строк и «b» столбцов. Здесь строки и столбцы соответствуют узлам и ветвям ориентированного графа. Следовательно, порядок матрицы инцидентности будет n × b .

Элементы матрицы инцидентности будут иметь одно из этих трех значений: +1, -1 и 0.

• Если ток ветви уходит из выбранного узла, то значение элемента будет +1.

• Если ток ветви поступает в направлении выбранного узла, то значение элемента будет равно -1.

• Если ток ветви не входит в выбранный узел и не выходит из выбранного узла, тогда значение элемента будет 0.

Если ток ветви уходит из выбранного узла, то значение элемента будет +1.

Если ток ветви поступает в направлении выбранного узла, то значение элемента будет равно -1.

Если ток ветви не входит в выбранный узел и не выходит из выбранного узла, тогда значение элемента будет 0.

Процедура поиска Матрицы заболеваемости

Выполните следующие действия, чтобы найти матрицу инцидентности ориентированного графа.

• Выберите узел во время данного ориентированного графа и заполните значения элементов матрицы инцидентности, соответствующих этому узлу, в строке.

• Повторите вышеуказанный шаг для всех узлов данного ориентированного графа.

Выберите узел во время данного ориентированного графа и заполните значения элементов матрицы инцидентности, соответствующих этому узлу, в строке.

Повторите вышеуказанный шаг для всех узлов данного ориентированного графа.

пример

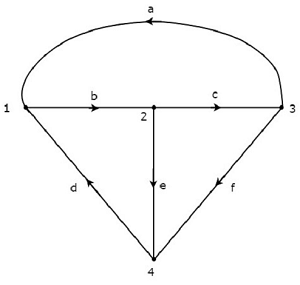
Рассмотрим следующий ориентированный граф .

Матрица инцидентности, соответствующая приведенному выше ориентированному графу, будет

$$A = \ begin {bmatrix} -1 & 1 & 0 & -1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 & -1 \ end {bmatrix}$$

Строки и столбцы вышеприведенной матрицы представляют узлы и ветви данного ориентированного графа. Порядок этой матрицы инцидентности составляет 4 × 6.

Соблюдая приведенную выше матрицу инцидентности, можно сделать вывод, что сумма элементов столбца матрицы инцидентности равна нулю. Это означает, что ток ветвления выходит из одного узла и входит только в другой отдельный узел.

Примечание. Если данный граф является неориентированным типом, преобразуйте его в ориентированный граф, представив стрелки на каждой его ветви. Мы можем рассмотреть произвольное направление протекания тока в каждой ветви.

Матрица фундаментальной петли

Фундаментальный цикл или f-цикл представляет собой цикл, который содержит только одну ссылку и одну или несколько веток. Итак, количество f-циклов будет равно количеству ссылок. Матрица фундаментальной петли представлена ​​буквой B. Она также называется матрицей фундаментальной цепи и матрицей Tie-set. Эта матрица дает соотношение между токами ветвления и токами звеньев.

Если в ориентированном графе имеется n узлов и ветви b присутствуют, то количество ссылок, присутствующих в совместном дереве, которое соответствует выбранному дереву данного графа, будет b-n + 1.

Таким образом, матрица основного цикла будет иметь строки «b-n + 1» и столбцы «b». Здесь строки и столбцы соответствуют ссылкам co-дерева и ветвей данного графа. Следовательно, порядок матрицы фундаментального цикла будет (b — n + 1) × b .

Элементы матрицы основного цикла будут иметь одно из этих трех значений: +1, -1 и 0.

• Значение элемента будет +1 для ссылки выбранного f-цикла.

• Значение элементов будет равно 0 для остальных ссылок и веток, которые не являются частью выбранного f-цикла.

• Если направление тока ветки выбранного f-контура совпадает с направлением тока линии f-контура, то значение элемента будет +1.

• Если направление тока ветки выбранного f-петли противоположно направлению тока звена f-петли, тогда значение элемента будет -1.

Значение элемента будет +1 для ссылки выбранного f-цикла.

Значение элементов будет равно 0 для остальных ссылок и веток, которые не являются частью выбранного f-цикла.

Если направление тока ветки выбранного f-контура совпадает с направлением тока линии f-контура, то значение элемента будет +1.

Если направление тока ветки выбранного f-петли противоположно направлению тока звена f-петли, тогда значение элемента будет -1.

Процедура поиска матрицы фундаментальных циклов

Выполните следующие шаги, чтобы найти матрицу фундаментального цикла данного ориентированного графа.

• Выберите дерево заданного ориентированного графа.

• Включая одну ссылку за раз, мы получим один f-цикл. Заполните значения элементов, соответствующих этому f-циклу, в строке матрицы фундаментального цикла.

• Повторите вышеуказанный шаг для всех ссылок.

Выберите дерево заданного ориентированного графа.

Включая одну ссылку за раз, мы получим один f-цикл. Заполните значения элементов, соответствующих этому f-циклу, в строке матрицы фундаментального цикла.

Повторите вышеуказанный шаг для всех ссылок.

пример

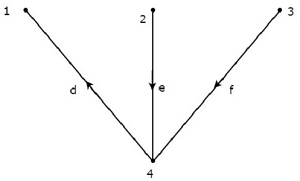
Взгляните на следующее дерево ориентированного графа , которое рассматривается для матрицы инцидентности.

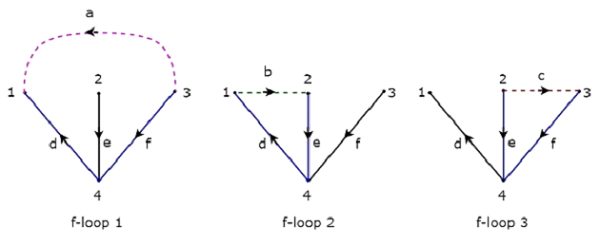
Вышеуказанное дерево содержит три ветви d, e & f. Следовательно, ветви a, b & c будут связями Co-Tree, соответствующими вышеуказанному дереву. Включая одну ссылку за раз на вышеуказанное дерево, мы получим один f-цикл . Таким образом, будет три f-петли , так как есть три ссылки. Эти три f-петли показаны на следующем рисунке.

На рисунке выше ветви, которые представлены цветными линиями, образуют f-петли. Мы получим значения построчных элементов матрицы Tie-set из каждого f-цикла. Таким образом, матрица Tieset рассмотренного выше дерева будет

$$B = \ begin {bmatrix} 1 & 0 & 0 & -1 & 0 & -1 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & -1 & 1 \ конец {bmatrix}$$

Строки и столбцы вышеприведенной матрицы представляют собой связи и ветви данного ориентированного графа. Порядок этой матрицы инцидентности составляет 3 × 6.

Количество матриц основного цикла ориентированного графа будет равно количеству деревьев этого ориентированного графа. Потому что каждое дерево будет иметь одну матрицу фундаментальных циклов.

Фундаментальная обрезная матрица

Фундаментальный набор срезов или набор f-срезов — это минимальное количество ветвей, которые удаляются из графа таким образом, что исходный граф станет двумя изолированными подграфами. Набор f-cut содержит только одну веточку и одну или несколько ссылок. Таким образом, количество наборов f-cut будет равно количеству веточек.

Матрица набора основных срезов обозначена буквой C. Эта матрица дает соотношение между напряжениями ответвления и напряжениями ветки.

Если в ориентированном графе имеется «n» узлов и «b» ветвей, то количество веток в выбранном дереве данного графа будет n-1. Таким образом, матрица основного набора сокращений будет иметь n-1 строки и столбцы b. Здесь строки и столбцы соответствуют веткам выбранного дерева и ветвям данного графа. Следовательно, порядок матрицы базового набора сечений будет (n-1) × b .

Элементы матрицы набора базовых сечений будут иметь одно из этих трех значений: +1, -1 и 0.

• Значение элемента будет +1 для ветки выбранного f-cutset.

• Значение элементов будет 0 для оставшихся веток и ссылок, которые не являются частью выбранного f-cutset.

• Если направление тока связи выбранного набора f-отрезков такое же, как и у потока веток f-отрезков, то значение элемента будет +1.

• Если направление тока связи выбранного набора f-cut противоположно направлению тока ветки f-cutset, то значение элемента будет -1.

Значение элемента будет +1 для ветки выбранного f-cutset.

Значение элементов будет 0 для оставшихся веток и ссылок, которые не являются частью выбранного f-cutset.

Если направление тока связи выбранного набора f-отрезков такое же, как и у потока веток f-отрезков, то значение элемента будет +1.

Если направление тока связи выбранного набора f-cut противоположно направлению тока ветки f-cutset, то значение элемента будет -1.

Процедура нахождения Фундаментальной Вырезанной Матрицы

Выполните следующие шаги, чтобы найти матрицу фундаментальных наборов сечений данного ориентированного графа.

• Выберите дерево заданного ориентированного графа и представьте ссылки пунктирными линиями.

• Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Заполните значения элементов, соответствующих этому набору f-сечений, в строке основной матрицы срезов.

• Повторите вышеуказанный шаг для всех веток.

Выберите дерево заданного ориентированного графа и представьте ссылки пунктирными линиями.

Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Заполните значения элементов, соответствующих этому набору f-сечений, в строке основной матрицы срезов.

Повторите вышеуказанный шаг для всех веток.

пример

Рассмотрим тот же ориентированный граф , который мы обсуждали в разделе матрицы инцидентности. Выберите ветви d, e & f этого ориентированного графа в виде веточек. Таким образом, оставшиеся ветви a, b & c этого ориентированного графа будут ссылками.

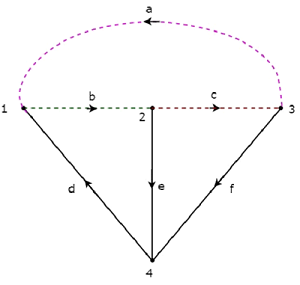
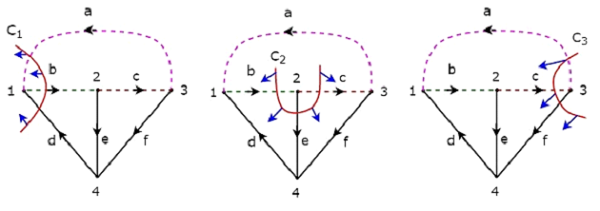
Веточки d, e & f представлены сплошными линиями, а ссылки a, b и c представлены пунктирными линиями на следующем рисунке.

Удалив одну веточку и необходимые ссылки за раз, мы получим один набор f-cut. Итак, будет три набора f-cut, так как есть три веточки. Эти три набора f-cut показаны на следующем рисунке.

У нас будет три набора f-cut, удалив набор веток и звеньев C ₁ , C ₂ и C ₃ . Мы получим значения построчных элементов матрицы фундаментальных наборов сечений из каждого набора f-срезов. Таким образом, основная матрица множества срезов рассмотренного выше дерева будет

$$C = \ begin {bmatrix} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \ конец {bmatrix}$$

Строки и столбцы вышеприведенной матрицы представляют собой веточки и ветви данного ориентированного графа. Порядок этой основной матрицы сечений равен 3 × 6.

Количество матриц Фундаментального набора сечений ориентированного графа будет равно количеству деревьев этого ориентированного графа. Потому что каждое дерево будет иметь одну матрицу Фундаментального среза.