Теория сетей — теорема суперпозиции

Теорема о суперпозиции основана на понятии линейности между откликом и возбуждением электрической цепи. В нем говорится, что отклик в конкретной ветви линейного контура, когда несколько независимых источников действуют одновременно, эквивалентен сумме откликов, связанных с каждым независимым источником, действующим одновременно.

В этом методе мы будем рассматривать только один независимый источник за один раз. Итак, мы должны исключить оставшиеся независимые источники из схемы. Мы можем устранить источники напряжения, замкнув их две клеммы и, аналогично, источники тока, открыв их две клеммы.

Следовательно, нам нужно найти ответ в определенной ветке «n» раз, если существует «n» независимых источников. Ответом в конкретной ветви может быть либо ток, протекающий через эту ветвь, либо напряжение через эту ветвь.

Процедура теоремы суперпозиции

Выполните следующие шаги, чтобы найти ответ в конкретной ветви, используя теорему суперпозиции.

Шаг 1 — Найти ответ в конкретной ветви, рассмотрев один независимый источник и исключив оставшиеся независимые источники, присутствующие в сети.

Шаг 2 — Повторите Шаг 1 для всех независимых источников, присутствующих в сети.

Шаг 3 — Добавьте все ответы, чтобы получить общий ответ в конкретной ветви, когда все независимые источники присутствуют в сети.

пример

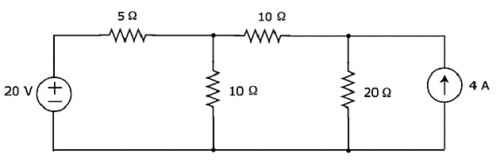
Найти ток, протекающий через резистор 20 Ом следующей цепи, используя теорему суперпозиции .

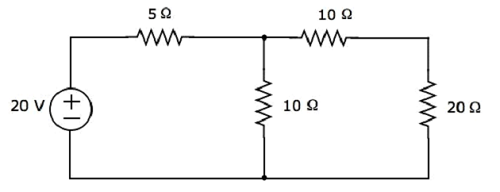
Шаг 1 — Найдем ток, протекающий через резистор 20 Ом, с учетом только источника напряжения 20 В. В этом случае мы можем устранить источник тока 4 А, разомкнув его. Модифицированная принципиальная схема показана на следующем рисунке.

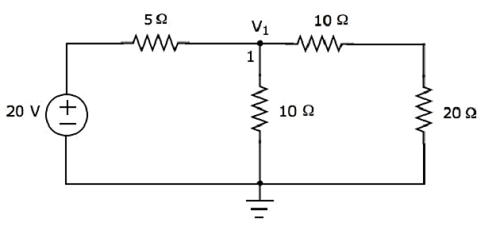
В вышеуказанной цепи есть только один главный узел, кроме Земли. Итак, мы можем использовать метод узлового анализа . Узел напряжения V ₁ обозначен на следующем рисунке. Здесь V ₁ — это напряжение от узла 1 относительно земли.

Узловое уравнение в узле 1

$$\ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0$$

$$\ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0$$

$$\ Rightarrow 10V_1 = 120$$

$$\ Rightarrow V_1 = 12V$$

Ток, протекающий через резистор 20 Ом, можно найти, выполнив следующее упрощение.

$$I_1 = \ frac {V_1} {10 + 20}$$

Подставим значение V ₁ в приведенное выше уравнение.

$$I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A$$

Следовательно, ток, протекающий через резистор 20 Ом, составляет 0,4 А , если рассматривать только источник напряжения 20 В.

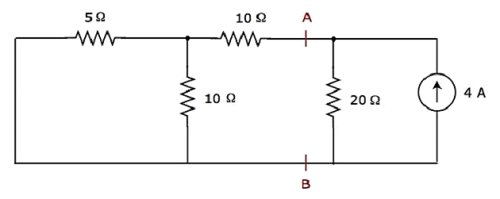
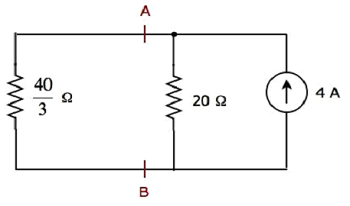
Шаг 2 — Давайте найдем ток, протекающий через резистор 20 Ом, рассматривая только источник тока 4 А. В этом случае мы можем устранить источник напряжения 20 В, сделав его коротким замыканием. Модифицированная принципиальная схема показана на следующем рисунке.

В приведенной выше схеме есть три резистора слева от клемм A и B. Мы можем заменить эти резисторы одним эквивалентным резистором . Здесь резисторы 5 Ом и 10 Ом подключены параллельно, и вся комбинация последовательно соединена с резистором 10 Ом.

Эквивалентное сопротивление слева от клемм A и B будет

$$R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega$$

Упрощенная принципиальная схема показана на следующем рисунке.

Мы можем найти ток, протекающий через резистор 20 Ом, используя принцип деления тока .

$$I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup$$

Замените IS=4A,R1= frac403 Omega$I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega$ и $R_2 = 20 \ Omega$ в вышеприведенном уравнении.

$$I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1.6 А$$

Следовательно, ток, протекающий через резистор 20 Ом, составляет 1,6 А , если рассматривать только источник тока 4 А.

Шаг 3 — Мы получим ток, протекающий через резистор 20 Ом данной цепи, сложив два тока, которые мы получили на шаге 1 и шаге 2. Математически это можно записать как

$$I = I_1 + I_2$$

Подставим значения I ₁ и I ₂ в приведенное выше уравнение.

$$I = 0,4 + 1,6 = 2 A$$

Следовательно, ток, протекающий через резистор 20 Ом данной цепи, составляет 2 А.

Примечание. Мы не можем напрямую применить теорему о суперпозиции, чтобы определить количество энергии, подаваемой на любой резистор, присутствующий в линейной цепи, просто добавляя мощности, подаваемые на этот резистор из-за каждого независимого источника. Скорее, мы можем рассчитать либо общий ток, протекающий через этот резистор, либо напряжение на нем, используя теорему суперпозиции, и исходя из этого, мы можем рассчитать количество энергии, подаваемой на этот резистор, используя $I ^ 2 R$ или $\ frac {V ^ 2} {R}$.