Теория сети — Фильтры

Фильтры, как следует из названия, они фильтруют частотные компоненты. Это означает, что они допускают определенные частотные компоненты и / или отклоняют некоторые другие частотные компоненты.

В этой главе давайте поговорим о пассивных фильтрах . Это электрические цепи или сети, имеющие пассивные элементы, такие как резистор, катушка индуктивности и конденсатор.

Типы фильтров

Фильтры в основном подразделяются на четыре типа в зависимости от разрешенной полосы частот и / или полосы отклоняющих частот. Ниже приведены типы фильтров.

• Фильтр низких частот
• Фильтр верхних частот
• Полосовой фильтр
• Band Stop Filter

Фильтр низких частот

Фильтр низких частот, как следует из названия, позволяет (пропускает) только низкочастотные компоненты. Это означает, что он отклоняет (блокирует) все другие высокочастотные компоненты.

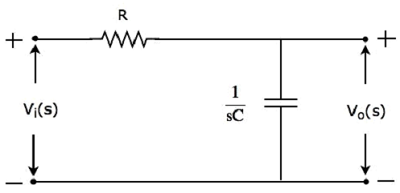
Схема s-домена (сеть) фильтра нижних частот показана на следующем рисунке.

Он состоит из двух пассивных элементов резистора и конденсатора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на конденсаторе.

Здесь $V_i (s)$ и $V_o (s)$ — преобразования Лапласа входного напряжения, $v_i (t)$ и выходного напряжения, $v_o (t)$ соответственно.

Передаточная функция вышеуказанной сети

$$H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {\ frac {1} {sC}} {R + \ frac {1} {sC}}$$

$$\ Rightarrow H (s) = \ frac {1} {1 + sCR}$$

Замените $s = j \ omega$ в приведенном выше уравнении.

$$H (j \ omega) = \ frac {1} {1 + j \ omega CR}$$

Величина передаточной функции

$$ | H (j \ omega) | = \ frac {1} {\ sqrt {(1 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 1.

• При $\ omega = \ frac {1} {CR}$ величина передаточной функции равна 0,707.

• При ω = ∞ величина передаточной функции равна 0.

При ω = 0 величина передаточной функции равна 1.

При $\ omega = \ frac {1} {CR}$ величина передаточной функции равна 0,707.

При ω = ∞ величина передаточной функции равна 0.

Следовательно, величина передаточной функции фильтра нижних частот будет варьироваться от 1 до 0, так как ω изменяется от 0 до ∞.

Фильтр верхних частот

Фильтр верхних частот, как следует из названия, разрешает (пропускает) только высокочастотные компоненты. Это означает, что он отклоняет (блокирует) все низкочастотные компоненты.

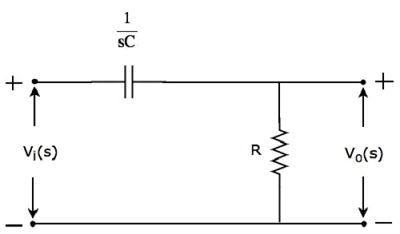
Принципиальная схема s-домена (сеть) фильтра верхних частот показана на следующем рисунке.

Он состоит из двух пассивных элементов — конденсатора и резистора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на резисторе.

Здесь $V_i (s)$ и $V_o (s)$ — преобразования Лапласа входного напряжения, $v_i (t)$ и выходного напряжения, $v_o (t)$ соответственно.

Передаточная функция вышеуказанной сети

$$H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {R} {R + \ frac {1} {sC}}$$

$$\ Rightarrow H (s) = \ frac {sCR} {1 + sCR}$$

Замените $s = j \ omega$ в приведенном выше уравнении.

$$H (j \ omega) = \ frac {j \ omega CR} {1 + j \ omega CR}$$

Величина передаточной функции

$$ | H (j \ omega) | = \ frac {\ omega CR} {\ sqrt {(1 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 0.

• При $\ omega = \ frac {1} {CR}$ величина передаточной функции равна 0,707.

• При ω = ∞ величина передаточной функции равна 1.

При ω = 0 величина передаточной функции равна 0.

При $\ omega = \ frac {1} {CR}$ величина передаточной функции равна 0,707.

При ω = ∞ величина передаточной функции равна 1.

Следовательно, величина передаточной функции фильтра верхних частот будет варьироваться от 0 до 1, так как ω изменяется от 0 до ∞.

Полосовой фильтр

Полосовой фильтр, как следует из названия, позволяет (пропускает) только одну полосу частот. В общем, эта полоса частот находится между низкочастотным диапазоном и высокочастотным диапазоном. Это означает, что этот фильтр отклоняет (блокирует) как низкочастотные, так и высокочастотные компоненты.

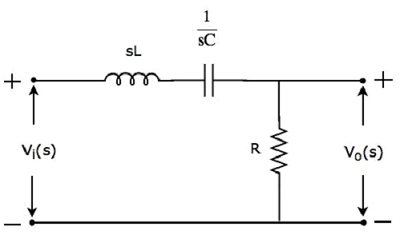
Принципиальная схема s-домена (сеть) полосового фильтра показана на следующем рисунке.

Он состоит из трех пассивных элементов индуктора, конденсатора и резистора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на резисторе.

Здесь $V_i (s)$ и $V_o (s)$ — преобразования Лапласа входного напряжения, $v_i (t)$ и выходного напряжения, $v_o (t)$ соответственно.

Передаточная функция вышеуказанной сети

$$H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {R} {R + \ frac {1} {sC} + sL}$$

$$\ Rightarrow H (s) = \ frac {s CR} {s ^ 2 LC + sCR + 1}$$

Замените $s = j \ omega$ в приведенном выше уравнении.

$$H (j \ omega) = \ frac {j \ omega CR} {1 - \ omega ^ 2 LC + j \ omega CR}$$

Величина передаточной функции

$$ | H (j \ omega) | = \ frac {\ omega CR} {\ sqrt {(1 — \ omega ^ 2 LC) ^ 2 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 0.

• При $\ omega = \ frac {1} {\ sqrt {LC}}$ величина передаточной функции равна 1.

• При ω = ∞ величина передаточной функции равна 0.

При ω = 0 величина передаточной функции равна 0.

При $\ omega = \ frac {1} {\ sqrt {LC}}$ величина передаточной функции равна 1.

При ω = ∞ величина передаточной функции равна 0.

Следовательно, величина передаточной функции полосового фильтра будет варьироваться от 0 до 1 и от 1 до 0, так как ω изменяется от 0 до ∞.

Band Stop Filter

Фильтр остановки полосы, как следует из названия, отклоняет (блокирует) только одну полосу частот. В общем, эта полоса частот находится между низкочастотным диапазоном и высокочастотным диапазоном. Это означает, что этот фильтр допускает (пропускает) как низкочастотные, так и высокочастотные компоненты.

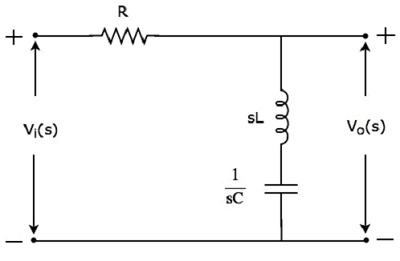
S-домен (сеть) принципиальной схемы и стоп-фильтра показан на следующем рисунке.

Он состоит из трех пассивных элементов: резистора, индуктора и конденсатора, которые соединены последовательно . Входное напряжение подается на всю эту комбинацию, а выход рассматривается как напряжение на комбинации индуктивности и конденсатора.

Здесь $V_i (s)$ и $V_o (s)$ — преобразования Лапласа входного напряжения, $v_i (t)$ и выходного напряжения, $v_o (t)$ соответственно.

Передаточная функция вышеуказанной сети

$$H (s) = \ frac {V_o (s)} {V_i (s)} = \ frac {sL + \ frac {1} {sC}} {R + sL + \ frac {1} {sC}}$$

$$\ Rightarrow H (s) = \ frac {s ^ 2 LC + 1} {s ^ 2 LC + sCR + 1}$$

Замените $s = j \ omega$ в приведенном выше уравнении.

$$H (j \ omega) = \ frac {1 - \ omega ^ 2 LC} {1 - \ omega ^ 2 LC + j \ omega CR}$$

Величина передаточной функции равна

$$ | H (j \ omega) | = \ frac {1 — \ omega ^ 2 LC} {\ sqrt {(1 — \ omega ^ 2 LC) ^ 2 + (\ omega CR) ^ 2}} $$

• При ω = 0 величина передаточной функции равна 1.

• При $\ omega = \ frac {1} {\ sqrt {LC}}$ величина передаточной функции равна 0.

• При ω = ∞ величина передаточной функции равна 1.

При ω = 0 величина передаточной функции равна 1.

При $\ omega = \ frac {1} {\ sqrt {LC}}$ величина передаточной функции равна 0.

При ω = ∞ величина передаточной функции равна 1.

Следовательно, величина передаточной функции полосового фильтра будет изменяться от 1 до 0 и от 0 до 1, так как ω изменяется от 0 до ∞.