Теория сети — пассивные элементы

В этой главе мы подробно обсудим пассивные элементы, такие как резистор, индуктор и конденсатор. Давайте начнем с резисторов.

резистор

Основная функциональность резистора либо противодействует, либо ограничивает протекание электрического тока. Следовательно, резисторы используются для ограничения величины тока и / или деления (разделения) напряжения.

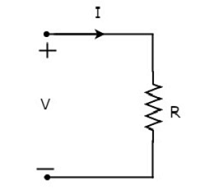
Пусть ток, протекающий через резистор, равен 1 А, а напряжение на нем составляет V вольт. Символ резистора вместе с током I и напряжением V показан на следующем рисунке.

Согласно закону Ома , напряжение на резисторе является произведением тока, протекающего через него, на сопротивление этого резистора. Математически это можно представить как

$V = IR$ Уравнение 1

$\ Rightarrow I = \ frac {V} {R}$ Уравнение 2

Где R сопротивление резистора.

Из уравнения 2 можно сделать вывод, что ток, протекающий через резистор, прямо пропорционален приложенному напряжению на резисторе и обратно пропорционален сопротивлению резистора.

Мощность в элементе электрической цепи может быть представлена ​​как

$P = VI$ Уравнение 3

Заменить уравнение 1 в уравнении 3.

$P = (IR) I$

$\ Rightarrow P = I ^ 2 R$ Уравнение 4

Заменить уравнение 2 в уравнении 3.

$P = V \ lgroup \ frac {V} {R} \ rgroup$

$\ Rightarrow P = \ frac {V ^ 2} {R}$ Уравнение 5

Таким образом, мы можем рассчитать величину мощности, рассеиваемой в резисторе, используя одну из формул, упомянутых в уравнениях 3-5.

Катушка индуктивности

В общем, индукторы будут иметь количество витков. Следовательно, они производят магнитный поток, когда ток течет через него. Таким образом, величина общего магнитного потока, создаваемого индуктором, зависит от тока, протекающего через него, и они имеют линейную зависимость.

Математически это можно записать как

 Psi alphaI $$\ Psi \: \ alpha \: I$$

$$\ Rightarrow \ Psi = LI$$

Куда,

• Ψ — общий магнитный поток

• L — индуктивность индуктора

Ψ — общий магнитный поток

L — индуктивность индуктора

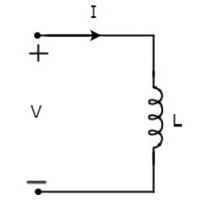
Пусть ток, протекающий через индуктор, равен 1 А, а напряжение на нем составляет V вольт. Символ индуктора вместе с током I и напряжением V показан на следующем рисунке.

Согласно закону Фарадея , напряжение на индуктивности может быть записано как

$$V = \ frac {d \ Psi} {dt}$$

Подставим Ψ = LI в приведенном выше уравнении.

$$V = \ frac {d (LI)} {dt}$$

$$\ Rightarrow V = L \ frac {dI} {dt}$$

$$\ Rightarrow I = \ frac {1} {L} \ int V dt$$

Из приведенных выше уравнений можно сделать вывод, что существует линейная зависимость между напряжением на индуктивности и током, протекающим через него.

Мы знаем, что мощность в элементе электрической цепи может быть представлена ​​как

$$P = VI$$

Замените $V = L \ frac {dI} {dt}$ в вышеприведенном уравнении.

$$P = \ lgroup L \ frac {dI} {dt} \ rgroup I$$

$$\ Rightarrow P = LI \ frac {dI} {dt}$$

Интегрируя вышеприведенное уравнение, мы получим энергию, запасенную в индукторе, в виде

$$W = \ frac {1} {2} LI ^ 2$$

Итак, индуктор накапливает энергию в виде магнитного поля.

Конденсатор

Как правило, конденсатор имеет две проводящие пластины, разделенные диэлектрической средой. Если положительное напряжение подается на конденсатор, то оно сохраняет положительный заряд. Точно так же, если отрицательное напряжение приложено к конденсатору, то это сохраняет отрицательный заряд.

Таким образом, количество заряда, хранящегося в конденсаторе, зависит от приложенного напряжения V на нем, и они имеют линейную зависимость. Математически это можно записать как

Q alphaV $$Q \: \ alpha \: V$$

$$\ Rightarrow Q = CV$$

Куда,

• Q — заряд, хранящийся в конденсаторе.

• С — емкость конденсатора.

Q — заряд, хранящийся в конденсаторе.

С — емкость конденсатора.

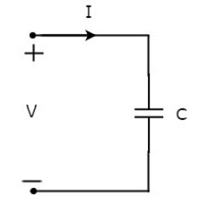
Пусть ток, протекающий через конденсатор, составляет 1 А, а напряжение на нем составляет V вольт. Символ конденсатора вместе с током I и напряжением V показан на следующем рисунке.

Мы знаем, что ток — это не что иное, как скорость потока заряда . Математически это можно представить как

$$I = \ frac {dQ} {dt}$$

Замените $Q = CV$ в приведенном выше уравнении.

$$I = \ frac {d (CV)} {dt}$$

$$\ Rightarrow I = C \ frac {dV} {dt}$$

$$\ Rightarrow V = \ frac {1} {C} \ int I dt$$

Из приведенных выше уравнений можно сделать вывод, что существует линейная зависимость между напряжением на конденсаторе и током, протекающим через него.

Мы знаем, что мощность в элементе электрической цепи может быть представлена ​​как

$$P = VI$$

Замените $I = C \ frac {dV} {dt}$ в вышеприведенном уравнении.

$$P = V \ lgroup C \ frac {dV} {dt} \ rgroup$$

$$\ Rightarrow P = CV \ frac {dV} {dt}$$

Интегрируя вышеприведенное уравнение, мы получим энергию, накопленную в конденсаторе как

$$W = \ frac {1} {2} CV ^ 2$$

Итак, конденсатор накапливает энергию в виде электрического поля.