Теория сети — серия резонанс

Резонанс возникает в электрических цепях из-за наличия элементов накопления энергии, таких как индуктор и конденсатор. Это фундаментальная концепция, основанная на том, что радиоприемники и телевизионные приемники спроектированы таким образом, чтобы они могли выбирать только желаемую частоту станции.

Существует два типа резонансов, а именно последовательный резонанс и параллельный резонанс. Они классифицируются на основе сетевых элементов, которые соединены последовательно или параллельно. В этой главе давайте поговорим о последовательном резонансе.

Схема последовательного резонанса

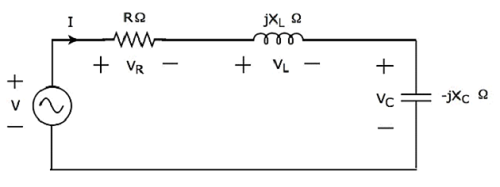
Если резонанс возникает в последовательной цепи RLC, то он называется последовательным резонансом . Рассмотрим следующую серию RLC-схемы , которая представлена ​​в векторной области.

Здесь пассивные элементы, такие как резистор, катушка индуктивности и конденсатор, соединены последовательно. Вся эта комбинация последовательно соединена с источником синусоидального напряжения.

Примените КВЛ вокруг петли.

$$V - V_R - V_L - V_C = 0$$

$$\ Rightarrow V - IR - I (j X_L) - I (-j X_C) = 0$$

$$\ Rightarrow V = IR + I (j X_L) + I (-j X_C)$$

$\ Rightarrow V = I [R + j (X_L - X_C)]$ Уравнение 1

Приведенное выше уравнение имеет вид V = IZ .

Следовательно, полное сопротивление Z последовательной цепи RLC будет

$$Z = R + j (X_L - X_C)$$

Параметры и электрические величины при резонансе

Теперь давайте по порядку выведем значения параметров и электрических величин при резонансе последовательной цепи RLC.

Резонансная частота

Частота, на которой возникает резонанс, называется резонансной частотой f _r . В последовательной цепи RLC резонанс возникает, когда мнимый член импеданса Z равен нулю, т. Е. Значение $X_L - X_C$ должно быть равно нулю.

$$\ Rightarrow X_L = X_C$$

Замените $X_L = 2 \ pi f L$ и $X_C = \ frac {1} {2 \ pi f C}$ в вышеприведенном уравнении.

$$2 \ pi f L = \ frac {1} {2 \ pi f C}$$

$$\ Rightarrow f ^ 2 = \ frac {1} {(2 \ pi) ^ 2 LC}$$

$$\ Rightarrow f = \ frac {1} {(2 \ pi) \ sqrt {LC}}$$

Следовательно, резонансная частота f _r последовательной цепи RLC равна

$$f_r = \ frac {1} {(2 \ pi) \ sqrt {LC}}$$

Где L — индуктивность индуктивности, а C — емкость конденсатора.

Резонансная частота f _r последовательной цепи RLC зависит только от индуктивности L и емкости C. Но это не зависит от сопротивления R.

полное сопротивление

Мы получили сопротивление Z цепи RLC серии как

$$Z = R + j (X_L - X_C)$$

Замените $X_L = X_C$ в приведенном выше уравнении.

$$Z = R + j (X_C - X_C)$$

$$\ Rightarrow Z = R + j (0)$$

$$\ Rightarrow Z = R$$

При резонансе импеданс Z последовательной RLC цепи равен значению сопротивления R , т. Е. Z = R.

Ток, протекающий по цепи

Замените $X_L - X_C = 0$ в уравнении 1.

$$V = I [R + j (0)]$$

$$\ Rightarrow V = IR$$

$$\ Rightarrow I = \ frac {V} {R}$$

Следовательно, ток, протекающий через последовательную RLC-цепь в резонансе, равен $\ mathbf {\ mathit {I = \ frac {V} {R}}}$.

В резонансе полное сопротивление последовательной цепи RLC достигает минимального значения. Следовательно, максимальный ток протекает через эту цепь при резонансе.

Напряжение на резисторе

Напряжение на резисторе

$$V_R = IR$$

Подставьте значение I в приведенное выше уравнение.

$$V_R = \ lgroup \ frac {V} {R} \ rgroup R$$

$$\ Rightarrow V_R = V$$

Следовательно, напряжение на резисторе в резонансе составляет V _R = V.

Напряжение на Индукторе

Напряжение на индуктивности

$$V_L = I (jX_L)$$

Подставьте значение I в приведенное выше уравнение.

$$V_L = \ lgroup \ frac {V} {R} \ rgroup (jX_L)$$

$$\ Rightarrow V_L = j \ lgroup \ frac {X_L} {R} \ rgroup V$$

$$\ Rightarrow V_L = j QV$$

Следовательно, напряжение на катушке индуктивности при резонансе составляет $V_L = j QV$.

Таким образом, величина напряжения на индуктивности в резонансе будет

$$ | V_L | = QV $$

Где Q — фактор качества, а его значение равно $\ frac {X_L} {R}$

Напряжение на конденсаторе

Напряжение на конденсаторе

$$V_C = I (-j X_C)$$

Подставьте значение I в приведенное выше уравнение.

$$V_C = \ lgroup \ frac {V} {R} \ rgroup (-j X_C)$$

$$\ Rightarrow V_C = -j \ lgroup \ frac {X_C} {R} \ rgroup V$$

$$\ Rightarrow V_C = -jQV$$

Таким образом, напряжение на конденсаторе в резонансе составляет $\ mathbf {\ mathit {V_C = -jQV}}$.

Таким образом, величина напряжения на конденсаторе в резонансе будет

$$ | V_C | = QV $$

Где Q — фактор качества, а его значение равно $\ frac {X_ {C}} {R}$

Примечание. Последовательная резонансная схема RLC называется схемой увеличения напряжения , поскольку величина напряжения на индуктивности и конденсаторе равна Q, умноженной на входное синусоидальное напряжение V.