Теория сети — отклик цепей переменного тока

В предыдущей главе мы обсудили переходную характеристику и реакцию установившегося состояния цепи постоянного тока. В этой главе давайте обсудим реакцию цепи переменного тока . Понятия как переходного отклика, так и отклика в стационарном состоянии, которые мы обсуждали в предыдущей главе, также будут здесь полезны.

Нахождение ответа серии RL Circuit

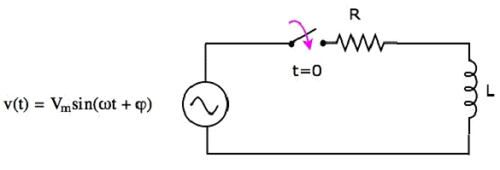
Рассмотрим следующую схему RL серии .

В вышеупомянутой схеме переключатель оставался открытым до t = 0, и он был закрыт при t = 0 . Таким образом, источник переменного напряжения, имеющий пиковое напряжение V _m вольт, не подключен к последовательной цепи RL до этого момента. Следовательно, через индуктор не протекает начальный ток .

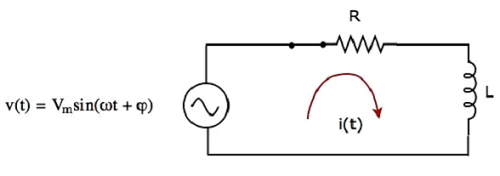
Принципиальная схема, когда переключатель находится в закрытом положении, показана на следующем рисунке.

Теперь ток i (t) течет во всей схеме, поскольку источник переменного напряжения, имеющий пиковое напряжение V _m вольт, подключен к последовательной цепи RL.

Мы знаем, что ток i (t), протекающий через вышеуказанную схему, будет иметь два члена, один из которых представляет переходную часть, а другой — стационарное состояние.

Математически это можно представить как

$i (t) = i_ {Tr} (t) + i_ {ss} (t)$ Уравнение 1

Куда,

• $i_ {Tr} (t)$ — переходная характеристика тока, протекающего по цепи.

• $i_ {ss} (t)$ — это установившаяся реакция тока, протекающего по цепи.

$i_ {Tr} (t)$ — переходная характеристика тока, протекающего по цепи.

$i_ {ss} (t)$ — это установившаяся реакция тока, протекающего по цепи.

В предыдущей главе мы получили переходный отклик тока, протекающего через последовательную цепь RL. Он имеет вид $Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup}$.

Замените $i_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup}$ в уравнении 1.

$i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss} (t)$ Уравнение 2

Расчет установившегося состояния тока

Если синусоидальный сигнал подается в качестве входа в линейную электрическую цепь, то он генерирует устойчивый выходной сигнал, который также является синусоидальным сигналом . И входной, и выходной синусоидальные сигналы будут иметь одинаковую частоту, но разные амплитуды и фазовые углы.

Мы можем рассчитать реакцию стационарного состояния электрической цепи, когда она возбуждается синусоидальным источником напряжения, используя метод преобразования Лапласа .

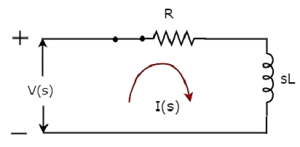
Схема s-домена, когда переключатель находится в закрытом положении, показана на следующем рисунке.

В приведенной выше схеме все величины и параметры представлены в s-области . Это преобразования Лапласа величин и параметров во временной области.

Передаточная функция вышеуказанной цепи

$$H (s) = \ frac {I (s)} {V (s)}$$

$$\ Rightarrow H (s) = \ frac {1} {Z (s)}$$

$$\ Rightarrow H (s) = \ frac {1} {R + sL}$$

Замените $s = j \ omega$ в приведенном выше уравнении.

$$H (j \ omega) = \ frac {1} {R + j \ omega L}$$

Величина $\ mathbf {\ mathit {H (j \ omega)}}$ равна

$$ | H (j \ omega) | = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$

Фазовый угол $\ mathbf {\ mathit {H (j \ omega)}}$ равен

$$\ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup$$

Мы получим ток установившегося состояния $i_ {ss} (t)$, выполнив следующие два шага:

• Умножьте пиковое напряжение входного синусоидального напряжения на величину $H (j \ omega)$.

• Добавьте фазовые углы входного синусоидального напряжения и $H (j \ omega)$.

Умножьте пиковое напряжение входного синусоидального напряжения на величину $H (j \ omega)$.

Добавьте фазовые углы входного синусоидального напряжения и $H (j \ omega)$.

Ток установившегося состояния $i_ {ss} (t)$ будет

$$i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup$$

Подставьте значение $i_ {ss} (t)$ в уравнение 2.

$i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup$ Уравнение 3

Мы знаем, что в цепи нет начального тока. Следовательно, замените t = 0 & i (t) = 0 в уравнении 3, чтобы найти значение постоянной, K.

$$0 = Ke ^ {- \ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega (0) + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup$$

$$\ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup$$

$$\ Rightarrow K = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup$$

Подставьте значение K в уравнение 3.

$i (t) = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup$ Уравнение 4

Уравнение 4 представляет ток, протекающий через последовательную цепь RL, когда он возбуждается синусоидальным источником напряжения. У него два срока. Первое и второе слагаемые представляют переходный отклик и отклик устойчивого состояния тока соответственно.

Мы можем пренебречь первым слагаемым в уравнении 4, потому что его значение будет намного меньше единицы. Таким образом, результирующий ток, протекающий через цепь будет

$$i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup$$

Он содержит только термин устойчивого состояния . Следовательно, мы можем найти только отклик устойчивого состояния цепей переменного тока и пренебречь переходным откликом от него.