Теория сети — отклик цепей постоянного тока

Если выход электрической цепи для входа изменяется во времени, то это называется временной реакцией . Время отклика состоит из следующих двух частей.

• Переходный ответ
• Устойчивый государственный ответ

В этой главе сначала давайте обсудим эти два отклика, а затем рассмотрим эти два отклика в последовательной цепи RL, когда она возбуждается источником постоянного напряжения.

Переходный ответ

После применения входа к электрической цепи, выходу требуется определенное время для достижения устойчивого состояния. Таким образом, выходной сигнал будет в переходном состоянии, пока он не перейдет в устойчивое состояние. Следовательно, отклик электрической цепи во время переходного состояния известен как переходный отклик .

Переходный отклик будет нулевым для больших значений «t». В идеале это значение t должно быть бесконечностью. Но практически пяти постоянных времени достаточно.

Присутствие или отсутствие переходных процессов

Переходные процессы происходят в ответе из-за внезапного изменения в источниках, которые применяются к электрической цепи и / или из-за действия переключения. Есть два возможных переключения. Это выключатель размыкания и замыкания.

• Переходная часть не будет присутствовать в ответе электрической цепи или сети, если она содержит только сопротивления. Потому что резистор имеет возможность регулировать любое количество напряжения и тока.

• Переходная часть возникает в ответе электрической цепи или сети из-за присутствия элементов накопления энергии, таких как индуктор и конденсатор . Потому что они не могут мгновенно изменить энергию, хранящуюся в этих элементах.

Переходная часть не будет присутствовать в ответе электрической цепи или сети, если она содержит только сопротивления. Потому что резистор имеет возможность регулировать любое количество напряжения и тока.

Переходная часть возникает в ответе электрической цепи или сети из-за присутствия элементов накопления энергии, таких как индуктор и конденсатор . Потому что они не могут мгновенно изменить энергию, хранящуюся в этих элементах.

Поведение индуктора

Предположим, что действие переключения происходит при t = 0. Ток индуктора не изменяется мгновенно, когда происходит действие переключения. Это означает, что значение тока индуктора сразу после действия переключения будет таким же, как и перед действием переключения.

Математически это можно представить как

$$i_L (0 ^ +) = i_L (0 ^ -)$$

Конденсаторное поведение

Напряжение на конденсаторе не изменяется мгновенно, подобно току индуктора, когда происходит переключающее действие. Это означает, что значение напряжения на конденсаторе сразу после переключения будет таким же, как и перед переключением.

Математически это можно представить как

$$v_c (0 ^ +) = v_c (0 ^ -)$$

Устойчивый государственный ответ

Часть временного отклика, которая остается даже после того, как переходный отклик стал нулевым значением для больших значений «t», называется устойчивым откликом . Это означает, что не будет никакой переходной части в ответе в устойчивом состоянии.

Поведение индуктора

Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько катушек индуктивности и резисторов (дополнительно) в течение длительного времени, то эта электрическая цепь или сеть, как говорят, находятся в устойчивом состоянии. Следовательно, энергия, запасенная в катушке индуктивности этой электрической цепи, максимальна и постоянна.

Математически это можно представить как

$W_L = \ frac {L {i_L} ^ 2} {2} =$ Максимум и константа

$\ Rightarrow i_L =$ Максимум и константа

Следовательно, индуктор действует как источник постоянного тока в устойчивом состоянии.

Напряжение на индуктивности будет

$$V_L = L \ frac {di_ {L}} {dt} = 0V$$

Таким образом, индуктор действует как короткое замыкание в устойчивом состоянии.

Конденсаторное поведение

Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько конденсаторов и резисторов (необязательно), в течение длительного времени, то говорят, что эта электрическая цепь или сеть находятся в устойчивом состоянии. Следовательно, энергия, запасенная в конденсаторе (-ах) этой электрической цепи, является максимальной и постоянной.

Математически это можно представить как

$W_c = \ frac {C {v_c} ^ 2} {2} =$ Максимум и константа

$\ Rightarrow v_c =$ Максимум и константа

Следовательно, конденсатор действует как источник постоянного напряжения в устойчивом состоянии.

Ток, протекающий через конденсатор, будет

$$i_c = C \ frac {dv_c} {dt} = 0A$$

Таким образом, конденсатор действует как разомкнутая цепь в устойчивом состоянии.

Нахождение ответа серии RL Circuit

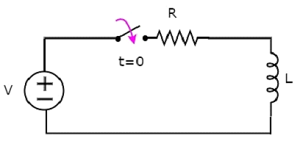
Рассмотрим следующую схему RL серии .

В вышеупомянутой схеме переключатель оставался открытым до t = 0, и он был закрыт при t = 0. Таким образом, источник постоянного напряжения, имеющий V вольт, не подключен к последовательной цепи RL до этого момента. Следовательно, через индуктор не протекает начальный ток .

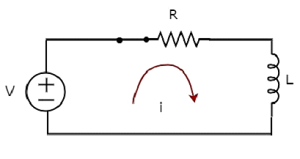
Принципиальная электрическая схема, когда переключатель находится в закрытом положении, показана на следующем рисунке.

Теперь ток i течет во всей схеме, поскольку источник постоянного напряжения, имеющий V вольт, подключен к последовательной цепи RL.

Теперь примените KVL вокруг петли.

$$V = Ri + L \ frac {di} {dt}$$

$\ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L}$ Уравнение 1

Вышеупомянутое уравнение является дифференциальным уравнением первого порядка, и оно имеет вид

$\ frac {dy} {dt} + Py = Q$ Уравнение 2

Сравнивая Уравнение 1 и Уравнение 2, мы получим следующие соотношения.

$$x = t$$

$$y = i$$

$$P = \ frac {R} {L}$$

$$Q = \ frac {V} {L}$$

Решение уравнения 2 будет

$ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k$ Уравнение 3

Где k постоянная

Подставим значения x, y, P & Q в уравнение 3.

$ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k$

$\ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + к$

$\ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k$

$\ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t$ Уравнение 4

Мы знаем, что в цепи нет начального тока. Следовательно, замените t = 0 и ? = 0 в уравнении 4, чтобы найти значение константы k .

$$0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)}$$

$$0 = \ frac {V} {R} + k (1)$$

$$k = - \ frac {V} {R}$$

Подставим значение k в уравнение 4.

$$i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t}$$

$$i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t}$$

Следовательно, ток, протекающий по цепи

$i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R}$ Уравнение 5

Итак, отклик цепи последовательного RL, когда она возбуждается источником постоянного напряжения, имеет следующие два члена.

• Первый член $- \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t}$ соответствует переходному ответу .

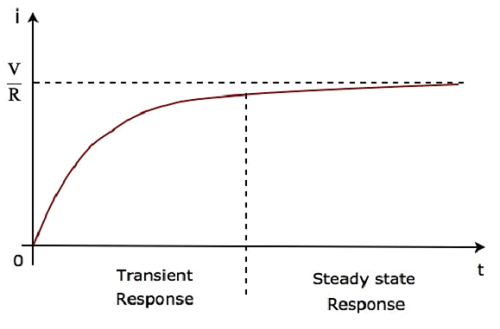
• Второе слагаемое $\ frac {V} {R}$ соответствует отклику установившегося состояния . Эти два ответа показаны на следующем рисунке.

Первый член $- \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t}$ соответствует переходному ответу .

Второе слагаемое $\ frac {V} {R}$ соответствует отклику установившегося состояния . Эти два ответа показаны на следующем рисунке.

Мы можем переписать уравнение 5 следующим образом:

$i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup$

$\ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup$ Уравнение 6

Где τ — постоянная времени, и ее значение равно $\ frac {L} {R}$.

И Уравнение 5, и Уравнение 6 одинаковы. Но мы можем легко понять вышеуказанную форму волны тока, протекающего по цепи из уравнения 6, подставив несколько значений t, таких как 0, τ, 2τ, 5τ и т. Д.

В приведенной выше форме волны тока, протекающего по цепи, переходный отклик будет представлять до пяти постоянных времени от нуля, тогда как отклик в установившемся режиме будет присутствовать с пяти постоянных времени.